20.2.1: Excess Pressure Inside Drops and Bubbles
- Page ID
- 8527
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The pressure inside a spherical drop is greater than the pressure outside. The way in which the excess pressure \(P\) depends on the radius \(a\) of the drop, and the surface tension \( \gamma\) and density \( \rho \) of the liquid is amenable to dimensional analysis. One can suppose that \( P \propto a^\alpha \gamma^\beta\rho^\delta, \) after which I leave it to the reader to show that \(\alpha = −1, \beta = 1, \delta = 0\), and therefore \( P \propto \gamma/ a \).
However, it is also quite easy to calculate the excess pressure (other than as a mere proportionality) in terms of the surface tension and the radius of the drop. In Figure XX.2 I have divided a spherical drop of radius \(a\) into two hemispheres, and we are going to consider the equilibrium of the upper hemisphere.
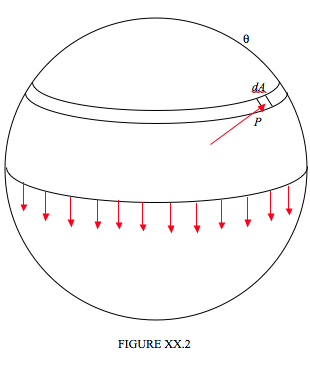
The upper hemisphere is being pulled down by surface tension all round the base of the hemisphere, and this downward force is equal to the circumference of the base times the surface tension, or \(2\pi \gamma a\). If the excess pressure inside the drop is \(P\), the upward component of the force due to this pressure is equal to \(P\) times the area of the base, \(\pi a^2\). In case this is not obvious, consider an elemental area \(dA\) as shown, at a spherical angle \( \theta \) from the top of the drop. The force on this element is equal to \(PdA\). The upward component of this force is \(P \cos \theta dA \), and this is equal to \(P\) times the horizontal projection of \(dA\). Now you are welcome to do a nice double integration over the hemisphere, but since this (i.e " this is equal to \(P\) times the horizontal projection of \(dA\) ") is true for every elemental area over the surface of the hemisphere, the total upward force must be equal to \(P\) times the area of the base. Thus \(2\pi \gamma a = \pi a2P \), and so the excess pressure inside the drop is
\[P = \frac{2 \gamma}{a} \label{20.2.2}\tag{20.2.2} \]
The smaller the drop, the greater the excess pressure. You may regard this as an explanation as to why droplets cannot form from a vapor unless there is a dust nucleus of finite size for them to condense upon. Of course, two molecules colliding with each other cannot in any case coalesce unless there is something to remove or absorb the kinetic energy.
The case of a nonspherical drop might be mentioned in passing. It is a well known result in geometry (or at least it is well known to those who already know it) that if \(z = z(x , y)\) is a nonspherical surface, and you take two vertical planes at right angles to each other, and if \(a_1\) and \(a_2\) are the radii of curvature of the intersections of the two planes with the surface, then \( \frac{1}{a_1} + \frac{1}{a_2} \) is independent of the orientations of the two planes, as long as they remain perpendicular to each other. In other words, \(a_1\) and \(a_2\) do not have to be the maximum and minimum radii of curvature. The excess pressure inside a nonspherical drop is
\[P = \gamma \left( \dfrac{1}{a_1} + \dfrac{1}{a_2}\right) \label{20.2.3}\tag{20.2.3} \]
What about the pressure inside a spherical bubble of air (or other gas) under water (or other liquid)? If we are hasty, we might suggest that, since this is the opposite situation to a liquid drop in air, maybe the pressure is less inside an underwater bubble. This would be a very hasty conclusion, and quite wrong. If you go through exactly the same argument as we did for a drop, considering the equilibrium of one hemisphere, you will see immediately that there is (as for the drop) an excess pressure inside the bubble given again by Equation \( \ref{20.2.2} \). And exactly the same would apply to a spherical drop of one liquid under the surface of a second liquid, if the two liquid are immiscible. But, rather than just repeat the identical derivation, let's try a different approach.
Let us imagine that we have a bubble of radius \(a\) in a liquid of surface tension \( \gamma\), and suppose that we are able, by means of a fine syringe, to inject some more air inside so as to increase the radius of the bubble by \(da\) at constant pressure and temperature. The surface area of a sphere of radius \(a\) is \(A = 4\pi a^2\), so, if we increase the radius by \(da\) we increase the surface area by \(8 \pi a da\), and we increase the volume by \( 4 \pi a 2 da\). The work done against the surface tension is \( 8 \pi γa da\), and this must also be equal to \(4 \pi Pa^2 da\), where \(P\) is the excess pressure inside the bubble. Equating these two expressions leads again to Equation \( \ref{20.2.2} \).
What about a hollow spherical soap bubble in air? Here the soap has two surfaces – inside and out. If you repeat either of the above derivations to this case, you will see that the excess pressure inside a hollow spherical soap bubble is
\[P = \frac{4 \gamma}{a} \label{20.2.4}\tag{20.2.4} \]


