03. Analysis Tools 2
- Page ID
- 664
Gravitational Potential Energy
In any situation in which an object changes its height above the surface of the earth, the force of gravity does work on the object. It is possible to calculate this work in general, and to rewrite the work-energy relation in such a way as to incorporate the effects of this work. This is referred to as constructing apotential energy function for the work done by gravity.
Let’s imagine an object of mass, m, located an initial height, hi, above the zero of a vertical coordinate system, with the upward direction designated positive. It moves to a final height of hf.
The “mgh” terms are referred to as gravitational potential energy. Thus, the work done by gravity can be thought of as changing the gravitational potential energy of the object. Let’s plug the above result into the work-energy relation:
Therefore, this final relation:
initial energy + work = final energy
can be used in place of the standard work-energy relation provided:
- You do not include the force of gravity a second time by calculating the work done by gravity. Basically, in this relationship gravity is no longer thought of as a force that does work on objects but rather as a source of potential energy.
- You calculate the initial and final heights, hi and hf, using a coordinate system in which the upward direction is positive.
Applying Work-Energy with Gravitational Potential Energy
Let’s use the work-energy relation, with gravitational potential energy terms, to re-analyze the previous scenario:
A 0.35 kg model rocket is fitted with an engine that produces a thrust of 11.8 N for 1.8 s. The rocket is launched vertically upward.
We apply work-energy between the following two events:
Event 1: The instant the engine is ignited.
Event 2: The instant the rocket reaches its maximum height.
During this time interval, the force of the exhaust gases only act on the rocket for a portion of the entire displacement, namely 39 m. Remember, the force of gravity does not do work in this way of modeling nature, rather the gravitational energy of the rocket changes as it changes its elevation.
Setting the initial elevation of the rocket equal to zero:
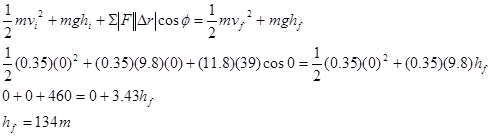
results in, of course, the same maximum height reached by the rocket.


