19.8: Contracted and Extended Cycloids
( \newcommand{\kernel}{\mathrm{null}\,}\)
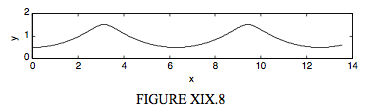
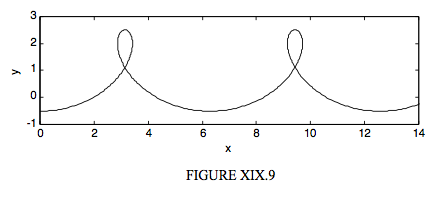
As in Section 19.1, we consider a circle of radius a rolling to the right on the line y=2a. The point P is initially below the centre of the circle, but, instead of being on the rim of the circle, its distance from the centre of the circle is r. If r<a, the path described by P will be a contracted cycloid; if r>a, the path is an extended cycloid. (I think there’s a case for using this nomenclature the other way round, but most authors seem to use “contracted” for r<a and “extended” for r>a.) It should not take long to be convinced, by arguments similar to those in Section 19.1, that the parametric equations to a contracted or extended cycloid are
x=2aθ+rsin2θ
and
y=a−rcos2θ
These are illustrated in Figures XIX.8 and XIX.9 for a contracted cycloid with r=0.5a and an extended cycloid with r=1.5a.