13.2: Alternating Voltage across a Capacitor
( \newcommand{\kernel}{\mathrm{null}\,}\)
At any time, the charge Q on the capacitor is related to the potential difference V across it by Q=CV. If there is a current in the circuit, then Q is changing, and I=C˙V.
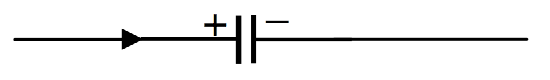
FIGURE XIII.3
Now suppose that an alternating voltage given by
V=ˆVsinωt
is applied across the capacitor. In that case the current is
I=CωˆVcosωt,
which can be written
I=ˆIcosωt,
where the peak current is
ˆI=CωˆV
and, of course
IRMS=CωVRMS.
The quantity 1/(Cω) is called the capacitive reactance XC. It is expressed in ohms (check the dimensions), and, the higher the frequency, the smaller the reactance. (The frequency ν is ω/(2π).)
When we come to deal with complex numbers, in the next and future sections, we shall incorporate a sign into the reactance. We shall call the reactance of a capacitor −1/(Cω) rather than merely 1/(Cω), and the minus sign will indicate to us that V lags behind I. The reactance of an inductor will remain Lω, since V leads on I.
Comparison of equations ??? and ??? shows that the current and voltage are out of phase, and that V lags behind I by 90°, as shown in Figure XIII.4.
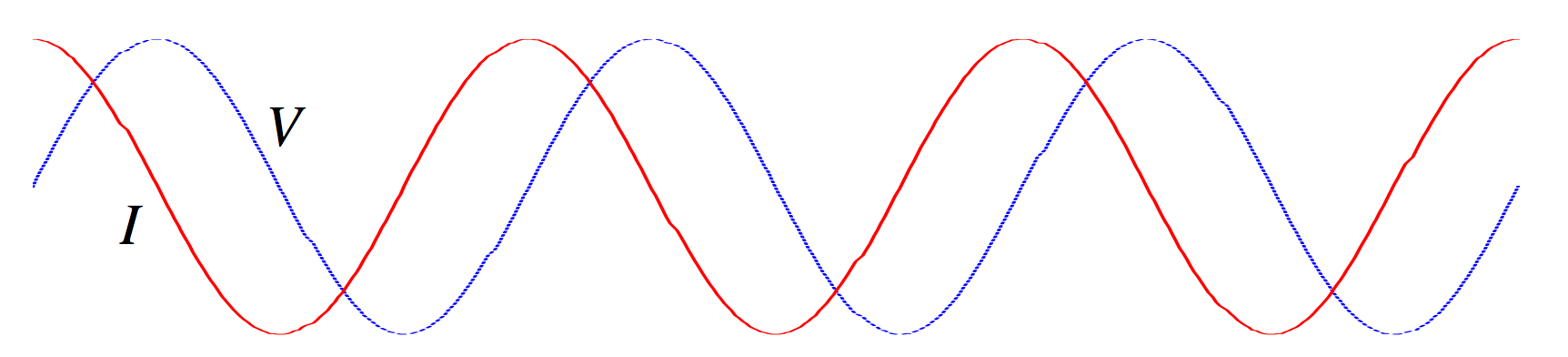
FIGURE XIII.4


