7.9: Magnetogyric Ratio
( \newcommand{\kernel}{\mathrm{null}\,}\)
The magnetic moment and the angular momentum are both important properties of subatomic particles. Each of them, however, depends on the angular speed of rotation of the particle. The ratio of magnetic moment to angular momentum, on the other hand, is independent of the speed of rotation, and tells us something about how the mass and charge are distributed within the particle. Also, it can be measured with higher precision than either the magnetic moment or the angular momentum separately. This ratio is called the magnetogyric ratio (or, perversely and illogically, by some, the "gyromagnetic ratio"). You should be able to show that the dimensions of the magnetogyric ratio are QM−1, and therefore the SI unit is C kg−1. I doubt, however, if many particle physicists use such simple units. They probably express magnetic moment in Bohr magnetons or nuclear magnetons and angular momentum in units of Planck's constant divided by 2π − but that is not our problem.
Let us calculate the magnetogyric ratio of a point charge and point mass moving in a circular orbit – rather like the electron moving around the proton in the simplest model of a hydrogen atom. We'll suppose that the angular speed in the orbit is ω and the radius of the orbit is a. The angular momentum is easy – it is just ma2ω. The frequency with which the particle (whose charge is Q) passes a given point in its orbit is ω/(2π), so the current is Qω/(2π). The area of the orbit is πa2 and so the magnetic moment of the orbiting particle is 12Qωa2. The magnetogyric ratio is therefore Q/(2m).
The magnetogyric ratio will be the same as this in any spinning body in which the distributions of mass density and charge density inside the body are the same. Consider, however, the magnetogyric ratio of a charged, spinning metal sphere. The mass is distributed uniformly throughout the sphere, but the charge all resides on the surface. We may then expect the magnetogyric ratio to be rather larger than Q/(2m).
The angular momentum is easy. It is just 25ma2ω. Now for the magnetic moment. Refer to Figure VII.6.
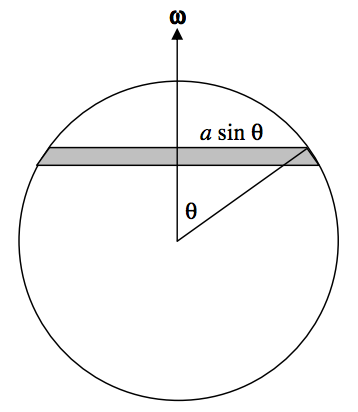
FIGURE VII.6
The area of the elemental zone shown is 2πa2sinθdθ. The area of the entire sphere is 4πa2, so the charge on the elemental zone is 12Qsinθdθ. The zone is spinning, as is the entire sphere, at an angular speed ω, so the current is
12Qsinθdθ×ω/(2π)=Qωsinθdθ4π
The area enclosed by the elemental zone is πa2sin2θ. The magnetic moment dpm of the zone is the current times the area enclosed, which is
dpm=14Qωa2sin3θdθ
The magnetic moment of the entire sphere is found by integrating this from θ = 0 to π, whence
pm=13Qωa2
The ratio of the magnetic moment to the angular momentum is therefore 5Q/(6m).
Those who are familiar with gyroscopic motion will know that if a spinning body of angular momentum L is subject to a torque τ, the angular momentum vector will not be constant in direction and indeed the rate of change of angular momentum will be equal to τ. Figure VII.7 is a reminder of the motion of a top in regular precession (that is, with no nutation).
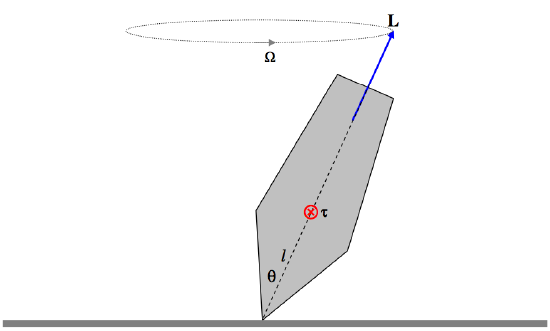
FIGURE VII.7
A study of Chapter 4 Section 4.10 of Classical Mechanics will be needed for a more detailed understanding of the motion of a top. The top is subject to a torque of magnitude mglsinθ. The torque can be represented by a vector τ directed into the plane of the paper. As drawn, the angular momentum vector L makes an angle θ with the gravitational field g, and it precesses about the vertical with an angular velocity Ω, the three vectors τ, L and Ω being related by τ=L×Ω. The magnitude of the angular momentum vector is therefore τ/(Lsinθ). But τ=mglsinθ, so that the precessional frequency is mgl/L, independent of θ. Likewise a charged spinning body with a magnetic moment of pm is a magnetic field B experiences a torque τ=pm×B, which is of magnitude pmBsinθ, and consequently its angular momentum vector precesses around B at an angular speed pmLB, independent of θ. (Verify that this has dimensions T−1.) The coefficient of B here is the magnetogyric ratio. The precessional speed can be measured very precisely, and hence the magnetogyric ratio can be measured correspondingly precisely. This phenomenon of "Larmor precession" is the basis of many interesting instruments and disciplines, such as the proton precession magnetometer, nuclear magnetic resonance spectroscopy and nuclear magnetic resonance imaging used in medicine. Because anything including the word "nuclear" is a politically incorrect phrase, the word "nuclear” is usually dropped, and nuclear magnetic resonance imaging is usually called just "magnetic resonance imaging", or MRI, which doesn't quite make sense, but at least is politically correct.


