8.3: Charged Particle in a Magnetic Field
( \newcommand{\kernel}{\mathrm{null}\,}\)
We already know that an electric current I flowing in a region of space where there exists a magnetic field B will experience a force that is at right angles to both I and B, and the force per unit length, F′, is given by
F′=I×B
and indeed we used this Equation to define what we mean by B. Equation ??? is illustrated in Figure VIII.1.
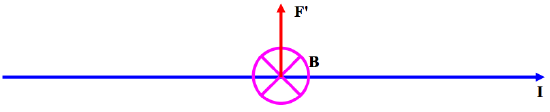
FIGURE VIII.1
The large cross in a circle is intended to indicate a magnetic field directed into the plane of the paper, and I and F′ show the directions of the current and the force.
Now we might consider the current to comprise a stream of particles, n of them per unit length, each bearing a charge q, and moving with velocity v (speed v). The current is then nqv, and Equation ??? then shows that the force on each particle is
F=qv×B.
This, then, is the Equation that gives the force on a charged particle moving in a magnetic field, and the force is known as the Lorentz force.
It will be noted that there is a force on a charged particle in a magnetic field only if the particle is moving, and the force is at right angles to both v and B.
As to the question: "Who's to say if the particle is moving?" or "moving relative to what?" – that takes us into very deep waters indeed. For an answer, I refer you to the following paper: Einstein, A., Zur Elektrodynamik Bewegter Körper, Annalen der Physik 17, 891 (1905).
Let us suppose that we have a particle, of charge q and mass m, moving with speed v in the plane of the paper, and that there is a magnetic field B directed at right angles to the plane of the paper. (If you are reading this straight off the screen, then read "plane of the screen"!) The particle will experience a force of magnitude qv B (because v and B are at right angles to each other), and this force is at right angles to the instantaneous velocity of the particle. Because the force is at right angles to the instantaneous velocity vector, the speed of the particle is unaffected. Its acceleration is constant in magnitude and therefore the particle moves in a circle, whose radius is determined by equating the force qv B to the mass times the centripetal acceleration. That is qv B=mv2/r, or
r=mvqB
If we are looking at the motion of some subatomic particle in a magnetic field, and we have reason to believe that the charge is equal to the electronic charge (or perhaps some small multiple of it), we see that the radius of the circular path tells us the momentum of the particle; that is, the product of its mass and speed. Equation ??? is quite valid for relativistic speeds, except that the mass that appears in the Equation is then the relativistic mass, not the rest mass, so that the radius is a slightly more complicated function of speed and rest mass.
If v and B are not perpendicular to each other, we may resolve v into a component v1 perpendicular to B and a component v2 parallel to B. The particle will then move in a helical path, the radius of the helix being mv2/(qB), and the centre of the circle moving at speed v2 in the direction of B.
The angular speed ω of the particle in its circular path is ω=v/r, which, in concert with Equation ???, gives
ω=qBm.
This is called the cyclotron angular speed or the cyclotron angular frequency. You should verify that its dimensions are T−1.
A magnetron is an evacuated cylindrical glass tube with two electrodes inside. One, the negative electrode (cathode) is a wire along the axis of the cylinder. This is surrounded by a hollow cylindrical anode of radius a. A uniform magnetic field is directed parallel to the axis of the cylinder. The cathode is heated (and emits electrons, of charge e and mass m) and a potential difference V is established across the electrodes. The electrons consequently reach a speed given by
eV=12mv2.
Because of the magnetic field, they move in arcs of circles. As the magnetic field is increased, the radius of the circles become smaller, and, when the diameter of the circle is equal to the radius a of the anode, no electrons can reach the anode, and the current through the magnetron suddenly drops. This happens when
12a=mveB.
Elimination of v from Equations ??? and ??? shows that the current drops to zero when
B=√8mVea2.
Those who are skilled in special relativity should try and do this with the relativistic formulas. In Equation ??? the right hand side will have to be (γ−1)m0c2, and in Equation ??? m will have to be replaced with γm0. I make the result
B=2√2m0c2eV+e2V2eac.
For small potential differences, eV is very much less than m0c2, and Equation ??? reduces to Equation ???.


