2.15: Appendix II- Legendre Transformations
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.15:_Appendix_II-_Legendre_Transformations), /content/body/p[1]/span, line 1, column 23
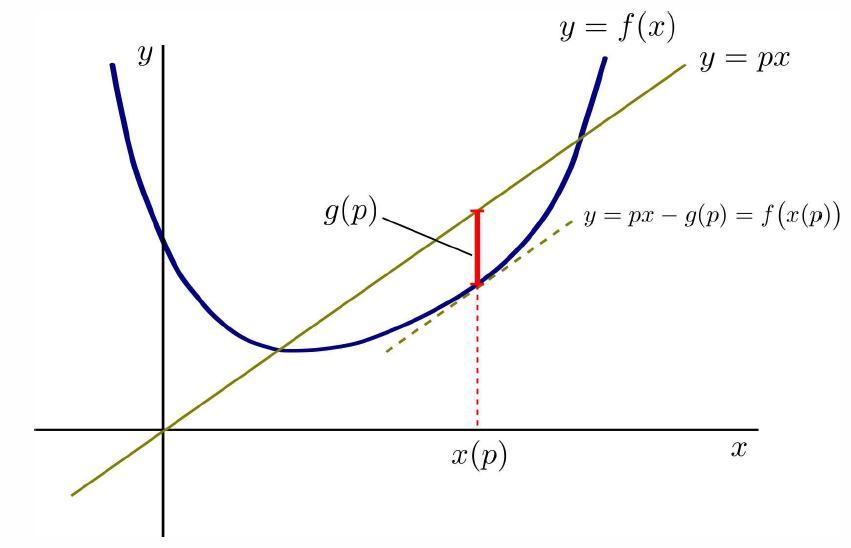
A convex function of a single variable f(x) is one for which f″ everywhere. The Legendre transform of a convex function f(x) is a function g(p) defined as follows. Let p be a real number, and consider the line y=px, as shown in Figure \PageIndex{1}. We define the point x(p) as the value of x for which the difference F(x,p)=px-f(x) is greatest. Then define g(p)=F\big(x(p),p\big).26 The value x(p) is unique if f(x) is convex, since x(p) is determined by the equation
f'\big(x(p)\big)=p\ .
Note that from p=f'\big(x(p)\big) we have, according to the chain rule,
{d\over dp}\,f'\big(x(p)\big)=f''\big(x(p)\big)\,x'(p)\qquad\Longrightarrow\qquad x'(p)=\Big[f''\big(x(p)\big)\Big]^{-1}\ .
From this, we can prove that g(p) is itself convex:
\begin{split} g'(p)&={d\over dp} \Big[ p\,x(p)-f\big(x(p)\big)\Big]\\ &=p\,x'(p) + x(p) - f'\big(x(p)\big)\,x'(p)= x(p)\ , \end{split}
hence
g''(p)=x'(p)=\Big[f''\big(x(p)\big)\Big]^{-1}>0\ .
In higher dimensions, the generalization of the definition f''(x)>0 is that a function F(x\ns_1,\ldots,x\ns_n) is convex if the matrix of second derivatives, called the Hessian,
H_{ij}(\Bx)={\pz^2 \!F\over\pz x\ns_i\,\pz x\ns_j}
is positive definite. That is, all the eigenvalues of H_{ij}(\Bx) must be positive for every \Bx. We then define the Legendre transform \BG(\Bp) as
\BG(\Bp)=\Bp\cdot\Bx-F(\Bx)
where
\Bp=\bnabla F\ .
Note that
dG=\Bx\cdot d\Bp + \Bp\cdot d\Bx - \bnabla F\cdot d\Bx = \Bx\cdot d\Bp\ ,
which establishes that G is a function of \Bp and that
{\pz G\over\pz p\ns_j}=x\ns_j\ . \label{LTcond}
Note also that the Legendre transformation is self dual, which is to say that the Legendre transform of G(\Bp) is F(\Bx): F\to G\to F under successive Legendre transformations.
We can also define a partial Legendre transformation as follows. Consider a function of q variables F(\Bx,\By), where \Bx=\{x\ns_1,\ldots,x\ns_m\} and \By=\{y\ns_1,\ldots,y\nd_n\}, with q=m+n. Define \Bp=\{p\ns_1,\ldots,p\ns_m\}, and
G(\Bp,\By)=\Bp\cdot\Bx-F(\Bx,\By)\ ,
where
p\ns_a={\pz F\over \pz x\ns_a}\qquad (a=1,\ldots,m)\ .
These equations are then to be inverted to yield
x\ns_a=x\ns_a(\Bp,\By)={\pz G\over \pz p\ns_a}\ .
Note that
p\ns_a={\pz F\over \pz x\ns_a}\,\big(\Bx(\Bp,\By),\By\big)\ .
Thus, from the chain rule,
\delta\ns_{ab}={\pz p\ns_a\over\pz p\ns_b}={\pz^2\!F\over\pz x\ns_a\,\pz x\ns_c}\,{\pz x\ns_c\over\pz p\ns_b} ={\pz^2\!F\over\pz x\ns_a\,\pz x\ns_c}\,{\pz^2\!G\over\pz p\ns_c\,\pz p\ns_b}\ ,
which says
{\pz^2 \! G\over\pz p\ns_a\,\pz p\ns_b}={\pz x\ns_a\over\pz p\ns_b}=\SK^{-1}_{ab}\ ,
where the m\times m partial Hessian is
{\pz^2\!F\over\pz x\ns_a\,\pz x\ns_b}={\pz p\ns_a\over\pz x\ns_b}=\SK\ns_{ab}\ .
Note that \SK\ns_{ab}=\SK\ns_{ba} is symmetric. And with respect to the \By coordinates,
{\pz^2 \! G\over\pz y\ns_\mu\,\pz y\ns_\nu}=-{\pz^2 \! F\over\pz y\ns_\mu\,\pz y\ns_\nu}=-\SL\ns_{\mu\nu}\ ,
where
\SL\ns_{\mu\nu}={\pz^2\!F\over\pz y\ns_\mu\,\pz y\ns_\nu}
is the partial Hessian in the \By coordinates. Now it is easy to see that if the full q\times q Hessian matrix H\ns_{ij} is positive definite, then any submatrix such as \SK\ns_{ab} or \SL\ns_{\mu\nu} must also be positive definite. In this case, the partial Legendre transform is convex in \{p\ns_1,\ldots,p\ns_m\} and concave in \{y\ns_1,\ldots,y\ns_n\}.


