2.5: Force and Potential Energy
- Page ID
- 2063
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A Beautiful Connection
There is a deep connection between force and potential energy. This relationship has a useful graphical representation that will help us better understand the spring-mass potential energy and, in Chapter 3, the potential energy associated with the bonding between atoms.
Graphed below is the potential energy of a spring-mass system vs. deformation amount of the spring. As was explained earlier, this is a second degree, or parabolic relationship. Marked on the figure are the positions where the force exerted by the spring has the greatest and the least values. If pulled or pushed to some value of the position y, what do we know about the restoring force of the spring?
We know intuitively that the spring will try to snap back to it's original shape -- that is, that it will tend to return to zero deformation. How can we confirm our intuitions from the graph? To answer, we'll introduce the connection between force and potential energy.
Force and Potential Energy
If the potential energy function U(x) is known, then the force at any position can be obtained by taking the derivative of the potential.
\[ F_{x} = -\frac{dU}{dx} \]
Graphically, this means that if we have potential energy vs. position, the force is the negative of the slope of the function at some point.
\[ F = -(slope) \]
The minus sign means that if the slope is positive, the force is to the left, and visa versa. This should make sense, because it says that the force will try to push the object back to lower potential. If it were the other way around, springs would stretch themselves out spontaneously and planets would fly away from each other!
Video: Test Your Understanding
Video: Lecture 4 part 3
This is a general result that is true for the force associated with any potential energy[i]. Disregarding the minus sign for a moment, this tells us that the steeper the slope of a PE curve plotted against its position variable, the greater the magnitude of the force. The restoring force of the spring (or anything that oscillates) will be zero when the slope is zero, which occurs at the equilibrium point, i.e., where the object comes to rest when it stops vibrating.
Using this knowledge, let's see how it makes perfect sense for the spring-mass potential graphed above. Starting qualitatively, the force should be maximum when the spring is most out of shape. The parabolic function has a slope which increases in magnitude the further from zero we go. Applying the idea that the magnitude of the slope tells us the magnitude of the force, we can tell from the graph that the force increases the further the spring is from equilibrium. Next, the force should be zero when the spring is in its equilibrium position. A quick look at the graph tells us that the slope of the curve at the origin is in fact zero. So far so good! Lastly, there's the minus sign. As the spring-mass is pulled to the right, the graph's slope becomes positive. The potential-energy-force relationship tells us that the force should then be negative, which means to the left. This should make perfect sense: the spring is stretched to the right, so it pulls left in an attempt to return to equilibrium.
We can quantitatively show just how right this relationships is. If we take our spring-mass potential energy function, then the force is
\[F_{y} = -\frac{dU}{dy} = -\frac{d}{dy} (\frac{1}{2}ky^{2}) = -ky \]
The final result is Hooke's law, the first equation introduced in our discussion of springs! Now that you're convinced that this relationship is real, let's see if we can understand why.
Why is this true?
It all boils down to the concepts of work and energy conservation. To understand, consider the following situation (pictured below). Imagine a box is lifted through a potential field, like lifting an object against gravity. Imagine also that the field is associated with a force, which is constant and pointing downwards at all points in space.
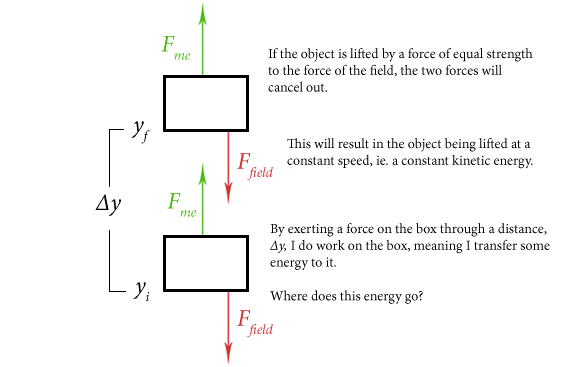
The energy cannot be going to kinetic energy, because by design the kinetic energy is constant. The energy also cannot be disappearing, because of energy conservation. The answer is that it is being transferred to potential energy.
The amount of work I do on the object is given by the force I exert times the distance I moved through:
\[W = F_{me} \cdot \Delta y \]
Since only myself and the field are acting on the object, this also must be the amount of potential energy the object gains. We can therefore replace the amount of work done by me, \(W\), with the amount of potential gained, \(\Delta U \). If we rearrange to solve for \(F_{me}\), we get:
\[F_{me} = \frac{ \Delta U}{ \Delta y} \]
However, what we wish to know isn't the force I exerted, but the force the field exerted. By the design of the situation, the force the field exerts is equal and opposite the force I exert, so
\[F_{field} = - \frac{ \Delta U}{ \Delta y} \]
To derive this result, I used a constant force field, but it applies even to changing ones, provided the blocky \(\Delta\)'s become sufficiently small, so that \(\frac{ \Delta U}{ \Delta y}\) becomes a derivative.
Example: Interpreting Bond Energy
Pictured is the real potential energy vs. separation relationship for two hydrogen atoms. What does the shape of the curve tell us about the behavior of the bond?
Treat the Curve Like a Roller Coaster Track
By applying the relationship between force and potential energy, you will eventually arrive upon an intuition which is akin to treating the curve like the tracks of a roller coaster. That is, you can visualize the behavior of the system by imagining the object as riding the curve like a cart subject to gravity.
What that would tell us here is that hydrogen atoms easily fall into bonds with each other. We know this because the hydrogen "cart" would easily slide into the bond well. We can also tell that it's nigh impossible to bring two hydrogen atoms too close together. Imagine trying to push a cart up that extremely tall, steep hill!
Stable and Unstable Equilibrium
There are certain modes or positions of special interest are called equilibrium. From a force perspective, an equilibrium occurs any time the total force acting on an object is zero. This includes when there are multiple forces acting on the object, all of which cancel out.
Example of stable equilibrium:
A spring is at its equilibrium position when there is no elastic restoring force.
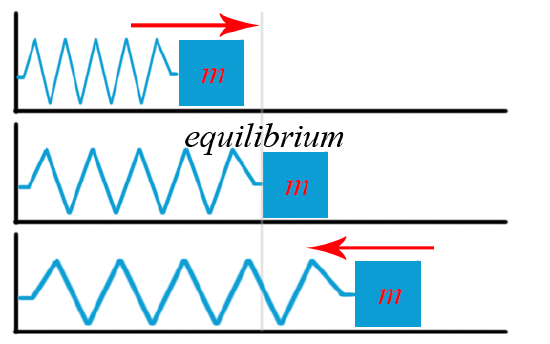
The spring reaches a stable equilibrium.
Each of the images below shows an example of equilibrium. They are, however, clearly very different situations. To get a more nuanced understanding of equilibrium than force alone can offer us, we turn to the connection between force and potential energy.
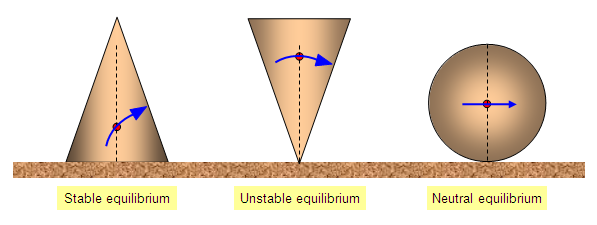
Definition: Stable Equilibrium
Stable equilibrium exists if the net force is zero, and small changes in the system would cause an increase in potential energy.
Definition: Unstable Equilibrium
Unstable equilibrium exists if the net force is zero, and small changes in the system would cause a decrease in potential energy.
Definition: Neutral Equilibrium
Neutral equilibrium exists if the net force is zero, and small changes in the system have no effect on the potential energy.
Equilibrium on a Potential Energy vs. Position Graph
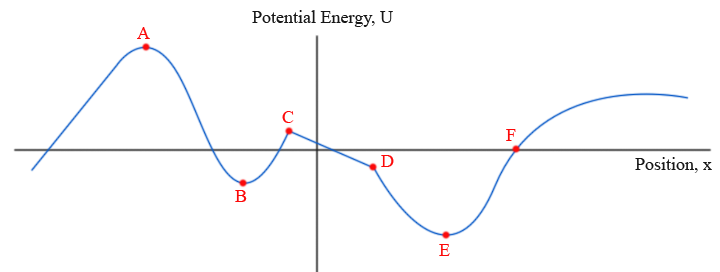
Equilibrium occurs where the force is zero. We now know that the (negative of) slope of a potential energy vs. position graph is force. The conclusion is that the equilibrium positions are the positions where the slope of the potential energy vs. position curve is zero.

We can quickly confirm that the red points above are labeled correctly by checking the definitions.
- The stable equilibrium should be at lower potential then any nearby point.
- The unstable equilibrium should be at higher potential energy than any nearby point.
- The neutral equilibrium should have the same potential energy as nearby points.
Exercise: Identifying Equilibrium
Which of the points are...
- In Stable Equilibrium
- In Unstable Equilibrium
- In Neutral Equilibrium
- Not In Equilibrium
[i] Everything we say here about the relation of force to potential energy is strictly true when the force depends on only one spatial dimension. That is, we consider the spring to move in only one direction in space. It the force depends on movement in two or three dimensions, then technically we say that force is the negative of the gradient of the potential. This is analogous to releasing a ball on a smooth hillside; the ball starts to roll in the direction of the steepest slope of the hill. In two or three dimensions, the force is the derivative of the potential in the direction of “steepest slope.”


