3.2 Phenomena and Data Patterns

Last updated
Save as PDF

Page ID: 2378

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Phenomena

The particulate nature of matter provides a model that allows explanations of a large range of phenomena that simply cannot be explained without invoking this fundamental idea regarding what matter is. In this chapter much of the focus will be simply developing a basic particle model, Intro Particle Model of Matter, sufficiently far so that, with a Particle Model of Bond Energy and a Particle Model of Thermal Energy it will be possible to develop explanations for many of the empirically determined thermal properties of matter encountered in Chapter 1. Specifically, how do we make sense of the range of thermal and bond energies we encountered in Chapter 1?

Data Patterns

In addition to the sampling of heat capacity data and heats of fusion and vaporization presented in Chapter 1, we would expect our models to provide us with the capability of explaining the heat capacity values, both at constant pressure and at constant volume for a large range of substances. Several of these data patterns are presented on this and the next page.

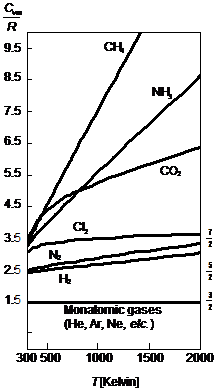
This first graph shows the constant volume molar heat capacity of several gases from room temperature up to several thousand kelvin. The values of the heat capacities have been divided by the gas constant, R. There are several obvious trends. The monatomic gases have the lowest molar constant-volume heat capacity at 3/2 R and the values are independent of temperature. Diatomic gases seem to have higher values starting at about 5/2 R, while polyatomic gases have significantly larger values, but also a much more pronounced temperature dependence. These are some of the trends our models should enable us to provide explanations for.

**Table 3.2.1:** Molar values of both Cp and Cv for Monatomic, Diatomic and Triatomic Gases at Room Temperature
gas	\( C_{mp} \)	\( C_{mv} \)	\( C_{mv}/R \)	\( C_{mp} - C_{mv}\)	\( (C_{mp} - C_{mv})/R \)
Monatomic
He	20.79	12.52	1.51	8.27	.99
Ne	20.79	12.68	1.52	8.11	.98
Ar	20.79	12.45	1.50	8.34	1.00
Li	20.79	12.45	1.50	8.34	1.00
Xi	20.79	12.52	1.51	8.27	.99
Diatomic
N₂	29.12	20.80	2.50	8.32	1.00
H₂	28.82	20.44	2.46	8.38	1.01
O₂	29.37	20.98	2.52	8.39	1.01
CO	29.04	20.74	2.49	8.30	1.00
Triatomic
CO₂	36.62	28.17	3.39	8.45	1.02
N₂O	36.90	28.39	3.41	8.51	1.02
H₂S	36.12	27.36	3.29	8.76	1.05

(This table is a version of a similar table in Physical Chemistry, Second Edition, by Joseph H. Noggle)

Several general trends are evident in the tabulated data. (Please refer to both tables of data–the table above and the table in Chapter 1.)

When the values of heats of melting and vaporization and specific heats of different substances are compared, there is a wide variation in quantities measured per kilogram. However, when these same quantities are measured per mole, much of the variation is removed.
The molar specific heat of many solids is very similar.
For monatomic substances, the value of molar specific heat of liquids is similar to the values for the solid phase.
The molar specific heats of polyatomic substances are greater in the liquid phase than the solid phase.
The specific heats of gases measured at constant pressure are greater than at constant volume.
Each type of gas, e.g., monatomic, has similar values of specific heats, and the values are ordered from smaller to larger as we go from monatomic to diatomic to triatomic.
The difference between \(C_{mp}\) and \(C_{mv}\) is very similar for all gases.
The same kinds of regularities observed in the molar specific heats do not appear in the melting and boiling points and in the heats of melting and vaporization. However, there are definite correlations between the melting and boiling points and the heats of melting and vaporization.