3.3 Intro Particle Model of Matter
- Page ID
- 2381
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this introductory model of the particle nature of matter we focus primarily on the force that acts between two atoms or molecules. We make extensive use of the relation of force to the potential energy describing the interaction between two atomic sized particles. Initially we assume the particles are electrically neutral, but we will see how to take this into account a little later in the chapter. The next two models will use the basic ideas established here to help us develop a much deeper understanding of both bond energy and thermal energy.
The particle model of matter that we introduce is the familiar picture of matter as composed of atoms and molecules. Our particle model for ordinary matter is simple and universal. It is not restricted to a particular kind of matter, but encompasses all ordinary matter. That is what makes this model so useful. Of course, being very general, it can’t predict many of the details that depend on the “particulars”, but it can predict many of the universal properties.
Construct Definitions
- Particle: This label applies to microscopic constituents of matter, typically an atom or molecule, but it could also refer, for example, to the constituents of the nucleus, if that were the focus of interest.
- Attractive and Repulsive Forces: Atomic sized particles exert forces on each other in the same way that large-scale objects do. These forces can be attractive or repulsive, which one typically depends on their separation.
- Interaction between two particles: The basis for making sense out of how particles interact is to focus on the interaction of only two particles at a time. There are several properties that keep reoccurring in our description of this interaction.\
- Center-to-center separation: We consistently refer to the distance between particles as being the center-to-center separation, rather than the distance between their surfaces. Usually we will use the symbol r to indicate this separation distance.
- Equilibrium position or equilibrium separation: When we are focusing on just two particles, we will find that there is often a “special” separation, often referred to as the equilibrium separation. The reason this separation is special is that at this equilibrium separation the interparticle force is zero. What does this say about the slope of the PE at this point? It has similarities to the spring-mass system in this respect. A mass hanging on a spring hangs at a particular “separation” from the point at which the spring is supported. This is a favored position. If the mass finds itself closer to the point of support, the “spring force” pushes it away, back toward the equilibrium position. Conversely, if it finds itself too far form the support, the spring force pulls it back toward the equilibrium position. The exact same thing happens with two atomic sized particles. We label the equilibrium separation for two particles with the symbol ro.
- Pair-wise Potential Energy: We will consistently refer to the potential energy between two atomic size particles as the pair-wise potential energy, PEpair-wise. This potential energy has a fairly generic shape to it that you need to become familiar with. In general terms, it becomes very repulsive if the two particles begin to get too close to each other. The potential has a minimum and becomes “horizontal”–slope is zero–at the two particle’s equilibrium separation. As the particles begin to separate, the potential at first “looks like” a spring-mass potential, but then begins to flatten out and becomes perfectly flat (horizontal, so zero force acting between the two particles here) once the separation is a few times that of the equilibrium separation, ro. The parameter that describes how “deep” the potential is, that is, the difference in energy between where the potential is flat at large separations and at its lowest value where the equilibrium separation occurs, is often called the “well depth” and designated with the lowercase Greek letter e. The well depth, e, is the magnitude of this energy difference, so is always a positive quantity.
- Single Particle Potential Energy: In a solid or liquid, each particle has multiple pair-wise interactions, because it has lots of neighbors to interact with. It will sometimes be useful to focus on just one particle at a time, and to “add up” all the interactions it has with its neighbors to obtain a potential energy function that describes the forces acting on just this one particle from all of its neighbors. We call this the single-particle potential energy to make it clear that it is not PEpair-wise.
Graphical Representation of the Pair-Wise Potential Energy
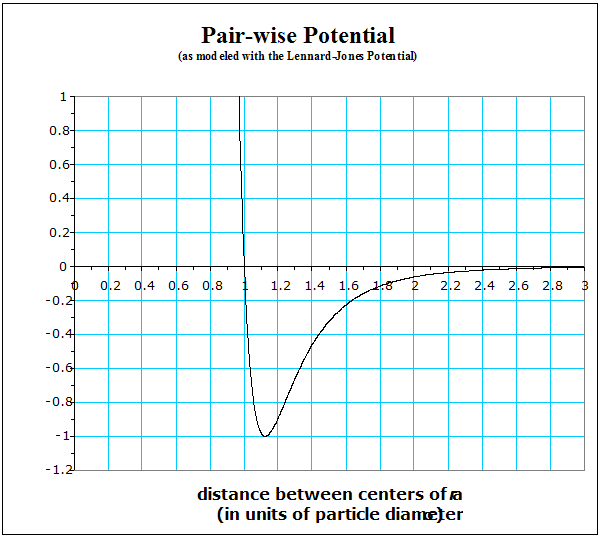
The PEpair-wise PE curve shown has the typical shape of almost all atomic-size pair-wise potentials. It has a simple mathematical form, so is useful for that reason alone. This particular shape describes rather well the interaction between the atoms of the noble elements (He, Ne, etc) in all their phases. Note that the equilibrium separation occurs at a slightly larger separation distance than one particle diameter, designated by the lower-case Greek sigma, s. If these particles acted like billiard balls, there would be a little space between them, even when they were as close as they “wanted” to get to each other.
It is customary, much to many beginners’ consternation, to define the zero of PEpair‑wise to be the value the PE has when the particles are separated by a great difference. Also notice how steep the curve gets as the particles begin to get closer than the equilibrium separation. Remember, a steep PE curve means a strong force, which is repulsive in this case. We will frequently return to this graph.
Meaning of the Model Relationships
1) All “normal” matter is comprised of tiny particles (atoms and molecules) that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another.
This is a slightly paraphrased quote from Nobel Laureate Richard Feynman in which he stated that if all scientific information were to be lost, these would be the most valuable ideas to pass on to future generations.
2) The part about the particles attracting and repelling each other is most easily visualized in terms of the slope of the pair-wise potential energy acting between the two particles. Be sure you review the previous chapter if you need to so that the relationship between force and PE ( |F| = |d(PE)/dr| ) is absolutely clear to you. There is no point in going any further, if you are still stumbling over this relationship.
3) Make sure you can use the relationship in (2) to explain to your fellow chemistry students (or your chemistry TA) the three bulleted features of the pair-wise potential using relationship (2) and the general shape of the pair-wise potential.
4) When there are many particles, the phase (s, l, g) of those particles depends on their total energy. At sufficiently high total energy, the particles are unbound and in the gas phase. At sufficiently low energy the particles are in the liquid or solid phase and are bound. The average particle-particle separation in the bound state is approximately equal to the separation corresponding to the minimum of the pair-wise potential energy. In the unbound state it is much greater than the separation corresponding to the minimum PE.
One common mistake that many students make is to attempt to ascribe macroscopic properties (like solid, liquid, gas) to the interaction of only a small number of particles using PEpair-wise. The macrostate of matter, whether it is in a solid, liquid or gas phase, for example, is due to the simultaneous interactions of something like 1025 pair-wise interactions if we have a mole of the substance. These ideas are not easy, so be patient. Initially, try to imagine a solid at very low temperatures. Each particle “wants” to be at the right distance with respect to all of its neighbors. If there is a way for the system to “get rid” of its energy (by giving it to some colder system, for example), it will continue to settle down and reduce its thermal energy. Eventually, all the random motion comes to a stop (if we can keep cooling the sample) and the particles find their “magic” places, each near the “bottom” of the PEpair-wise with each of each neighbors.
Now, imagine we start adding energy to the sample. All the particles begin acting like little spring-masses, oscillating back and forth around their equilibrium positions. Eventually they move sufficiently far, so that some “jump” out of where they are “supposed to be.” Particles at or near the surface might even leave the sample if their vibrations get vigorous enough. Picturing what happens when a substance melts, i.e., turns from a solid to a liquid, is difficult, even for the experts. Don’t worry about picturing that transition. But you can imagine continuing to add energy until all the particles, even 1023 particles, have sufficient energy to separate far apart from each other, causing them to be in the gas phase. Recall what value all ~1025 pair-wise potentials will have, if all particles are separated by many particle diameters. So, what is the bottom line here at this point in our making sense of all this? Without getting into a lot of detail, it should make sense to you that at some sufficiently low temperature, everything will be a solid and at some sufficiently high temperature, everything should be a gas. That is plenty for right now.
5) The interactions of one particle in a liquid or solid with all of its neighbors add together to form one three-dimensional potential energy for a particular particle with a minimum that defines the equilibrium position of that particle (where the net force due to all of the pair-wise interactions is zero). We refer to this potential as the single-particle potential energy to emphasize its distinction from the pair-wise potential energy.
6) Each particle in a solid or liquid oscillates in three dimensions about its equilibrium position as determined by its single-particle potential.
OK, so here is where we are attempting to make our mental picture a little clearer regarding what is happening to a single particle (which could be an atom or a tightly bound-together molecule) when it finds itself somewhere in the middle of similar particles in a solid or liquid. It really is acting like it is attached to a bunch of springs with all of its neighbors (and nearby neighbors). But here is the “really neat” thing. No matter how complicated the actual chemical bonds are, and no matter how many there are, or in what directions they point, they all add up to exactly what would happen if you had only three (that’s right, only three) little springs of exactly the right strength, one going out in each of the three x, y, and z directions of the three-dimensional space we seem to occupy in this universe (at least on our scale and on the scale of atoms and molecules). So the picture you want to get into your head is something like that shown below, remembering that the spring constant of the springs can be different in the three directions.

We will come back to this picture shortly when we make more sense of thermal energy.
But, what about the bond energy? Well, it really does depend on the real bonds, the real chemical bonds. However, we can develop reasonable estimates in terms of the well depths of the pair-wise interactions for the bond energy that work for practically all pure substances. Carrying out the analysis to make sense of bond energy and to make sense of thermal energy is what the next two models are about.


