11.2: The Dirac Equation
- Page ID
- 1254
Consider the motion of an electron in the absence of an electromagnetic field. In classical relativity, electron energy, \( E\) , is related to electron momentum, \( \frac{E}{c}=(p^2+ m_e^2\,c^2)^{1/2},\) \ref{1112}
where \( \left[p^0 - (p^1\,p^1+p^2\,p^2+p^3\,p^3+m_e^2\,c^2)^{1/2}\right]\psi = 0,\) \ref{1113}
where the \( p^0\) and the other \( \left[p^0 +(p^1\,p^1+p^2\,p^2+p^3\,p^3+m_e^2\,c^2)^{1/2}\right]\) then we obtain
\( p^0\) are also solutions of \ref{1113}.
The wave equation \ref{1114} is quadratic in \( \partial/\partial t\) , and, hence, in \( p^0\) . In order to ensure that this equation transforms in a simple way under a Lorentz transformation, we shall require it to be rational and linear in \( p^2\) , \( p^0\) . We are thus lead to a wave equation of the form
\( \alpha\) 's and \( p\) 's. Moreover, according to standard relativity, because we are considering the case of no electromagnetic field, all points in space-time must be equivalent. Hence, the \( \beta\) must also be independent of the \( \alpha\) 's and \( p\) 's and the \( \alpha\) 's and \( p^0 +\alpha_1\,p^1+\alpha_2\,p^2+\alpha_3\,p^3+\beta\,m_e\,c\) , we obtain
![$ \left[p^0\,p^0-\frac{1}{2}\sum_{i,j=1,3}\{\alpha_i,\alpha_j\}\,p^...
...m_{i=1,3}\{\alpha_i,\beta\}\,p^i\,m_e\,c-\beta^{\,2}\,m_e^2\,c^2\right]\psi= 0,$](http://farside.ph.utexas.edu/teaching/qm/lectures/img2589.png) \ref{1116}
\ref{1116}
where \( \{\alpha_i,\alpha_j\}\) \( \{\alpha_i,\beta\}\) \( \beta^{\,2}\) \( i,j=1,3\) . It is helpful to define the \( \mu=0,3\) , where
\( =\gamma^0,\) \ref{1120} \( = \gamma^0\,\gamma^i,\) \ref{1121}
for \( \{\gamma^{\,\mu},\gamma^\nu\} = 2\,g^{\,\mu\,\nu}.\) \ref{1122}
One way of satisfying the above anti-commutation relations is to represent the operators \( \gamma^{\,\mu}\) can be realized is four. In fact, it is easily verified that the \( \gamma^0\) \( \gamma^i\) \( i=1,3\) , satisfy the appropriate anti-commutation relations. Here, 0 and \( 1\) denote \( \sigma_i\) represent the \( \beta\) \( \alpha_i\) \( \gamma^0\) , \( \alpha_i\) , are all Hermitian matrices, whereas the \( \mu=1,3\) , are anti-Hermitian. However, the matrices \( \mu=0,3\) , are Hermitian. Moreover, it is easily demonstrated that
\( \mu=0,3\) .
Equation \ref{1115} can be written in the form
\( \partial_\mu\equiv \partial/\partial x^{\,\mu}\). Alternatively, we can write
\( \mbox{\boldmath\)\( {\bf p}=(p_x,p_y,p_z)=(p^1,p^2,p^3)\), and \( \alpha_i\) matrices. The previous expression is known as the Dirac equation. Incidentally, it is clear that, corresponding to the four rows and columns of the \( \psi\) must take the form of a \( x^{\,\mu}\) . We saw in Section 5.7 that the spin of the electron requires the wavefunction to have two components. The reason our present theory requires the wavefunction to have four components is because the wave equation \ref{1114} has twice as many solutions as it ought to have, half of them corresponding to negative energy states.
We can incorporate an electromagnetic field into the above formalism by means of the standard prescription \( p^{\,i}\rightarrow p^{\,i} +e\,A^{\,i}\) , where \( \phi\) the scalar potential, and \( {\bf A}\) the vector potential. This prescription can be expressed in the Lorentz invariant form
\( {\mit\Phi}^{\,\mu} = (\phi,c\,{\bf A})\) is the potential 4-vector. Thus, Equation \ref{1128} becomes
![$ \left[\gamma^{\,\mu}\left(p_\mu+\frac{e}{c}\,{\mit\Phi}_\mu\right...
...}\,\hbar\,\partial_\mu+\frac{e}{c}\,{\mit\Phi}_\mu\right)-m_e\,c\right]\psi=0 ,$](http://farside.ph.utexas.edu/teaching/qm/lectures/img2624.png) \ref{1131}
\ref{1131}
whereas Equation \ref{1129} generalizes to
![$ {\rm i}\,\hbar\,\frac{\partial\psi}{\partial t} =\left[-e\,\phi +...
...ox{\boldmath$\alpha$}\cdot({\bf p}+e\,{\bf A})+ \beta\,m_e\,c^2\right]\psi = 0.$](http://farside.ph.utexas.edu/teaching/qm/lectures/img2625.png) \ref{1132}
\ref{1132}
If we write the wavefunction in the spinor form
\( \psi= \left(\begin{array}{c}\psi_0\\ [0.5ex]\psi_1\\ [0.5ex]\psi_2\\ [0.5ex]\psi_3\end{array}\right)\) \ref{1133}
then the Hermitian conjugate of Equation \ref{1132} becomes
![$ -{\rm i}\,\hbar\,\frac{\partial\psi^\dag }{\partial t} =\psi^\dag...
...\boldmath$\alpha$}\cdot({\bf p} +{\bf e}\,{\bf A})+ \beta\,m_e\,c^2\right] = 0,$](http://farside.ph.utexas.edu/teaching/qm/lectures/img2627.png) \ref{1134}
\ref{1134}
where
\( \alpha_i\) and \( p^i\) and \( A^i\) .
It follows from \( \psi^\dag\left[\gamma^0\,\gamma^{\,\mu}\left({\rm i}\,\hbar\,\partial_\mu-\frac{e}{c}\,{\mit\Phi}_\mu\right)-\gamma^0\,m_e\,c\right]\psi=0.\)
\ref{1136}
The Hermitian conjugate of this expression is
\( \partial_\mu\) now acts backward on \( \gamma^0\,\gamma^{\,\mu}\) and \( \partial_\mu\,j^{\,\mu} = 0,\) \ref{1138}
where
\( j^{\,\mu} = (c\,\rho, {\bf j})\), where \( = \psi^\dag\,\psi,\) \ref{1140} \( = c\,\psi^\dag\,\gamma^0\,\gamma^i\,\psi = \psi^\dag\,c\,\alpha_i\,\psi,\) \ref{1141}
Equation \ref{1138} becomes
\( \rho({\bf x},t) = \vert\psi\vert^{\,2}\) as the relativistic probability density, and the vector field \( \vert\psi({\bf x},t)\vert\rightarrow 0\) as 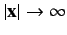 , yields \( t=0\), such that \( \rho\) as a probability density. Now, relativistic invariance demands that if the wavefunction is properly normalized in one particular inertial frame then it should be properly normalized in all inertial frames. This is the case provided that Equation \ref{1138} is Lorentz invariant (i.e., if it has the property that if it holds in one inertial frame then it holds in all inertial frames), which is true as long as the \( j^{\,\mu}\) transform as the contravariant components of a 4-vector under Lorentz transformation (see Exercise 4).
, yields \( t=0\), such that \( \rho\) as a probability density. Now, relativistic invariance demands that if the wavefunction is properly normalized in one particular inertial frame then it should be properly normalized in all inertial frames. This is the case provided that Equation \ref{1138} is Lorentz invariant (i.e., if it has the property that if it holds in one inertial frame then it holds in all inertial frames), which is true as long as the \( j^{\,\mu}\) transform as the contravariant components of a 4-vector under Lorentz transformation (see Exercise 4).
Contributors
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)


