Horsepower of an Engine
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introduction
This little document discusses the measurement of the power of an engine, particularly the horsepower of a car or motorcycle engine. The level of discussion is intended to be suitable for a beginning University-level Physics course.
Since the horsepower is based on the British system of units and is still commonly quoted by vehicle manufacturers, we will largely ignore SI units.
Equation numbers indicated with SJ are the numbers from R.A. Serway and J.W. Jewett, Principles of Physics: A Calculus-Based Text, 3rd ed.; equation numbers in parentheses are not from that text.
In order to effectively view this document, you will need to have the Flash player of at least Version 5 installed on your computer. The Flash player is available free from http://www.macromedia.com/.
Work & Power
When a force F acts in the direction of motion on an object, after the object has moved a distance Δr the work W done on the object is:
W=FΔr
 If the work is done on the object in a time Δt, then the power P is the rate at which the work is done:
If the work is done on the object in a time Δt, then the power P is the rate at which the work is done:
P=WΔt
The SI unit of power is the watt (W), named after James Watt, who invented the modern steam engine. The dimensions are N-m/s. The British units of power are ft-lb/sec.
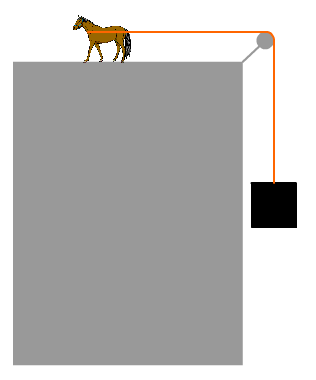
In about 1775, Watt introduced another unit for power: the horsepower (hp) . At that time, horses were used to lift coal up from a mine, as shown to the right.
Watt learned that "a strong horse could lift 150 pounds a height of 220 feet in 1 minute." He defined this as one horsepower.
1 hp is 150 lb x 220 ft / 60 seconds = 550 ft-lb/sec.
Measuring the Horsepower of an Engine
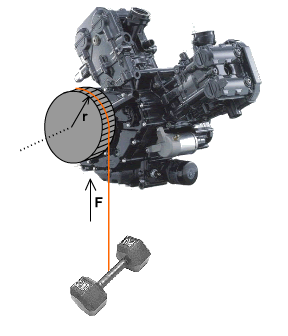 Direct Measurement
Direct Measurement
In principle, we could measure the horsepower of an engine the same way that Watt defined it: see how much weight the engine can lift a specified distance in a given time.
The animation to the right illustrates for a motorcycle engine. A pulley is mounted on the crankshaft, and turns with the engine. A weight is hanging from the pulley by a rope, and the engine lifts the weight at a constant speed. The weight has a magnitude of F and the pulley has a radius of r.
In practice, this method is very hard to use since a real engine turns at thousands of revolutions per minute.
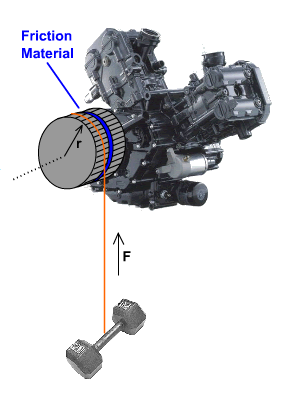 Indirect Measurement
Indirect Measurement
The way the measurement of the horsepower of an engine is typically performed is similar to the illustration to the right. The pulley mounted to the crankshaft of the engine is in contact with another pulley via a high-friction material between them. A weight is hung from the second pulley, and its mass is adjusted so that it is stationary.
The Mechanical Equivalent of Heat experiment in the laboratory uses a very similar technique. The Guide Sheet for the experiment (pdf, 297k) is here.
The engine shown in these animations is from a Suzuki SV650 motorcycle. The image is used by permission. The original site is: www.koups.com/sales/suzuki/sp...sv650_info.htm
In the Direct Measurment above, after one revolution of the engine, the work done by it is the circumference of the pulley times the force:
W1 rev=2πrF
When an applied force F acts at an angle φ with respect to the position vector r locating the point of application of the force, the torque is:
τ=rFsin(ϕ)
For the Direct Measurement, the angle φ is 90 degrees, so the torque being produced by the engine is r x F. Thus we re-write Eqn (1) in terms of the torque being produced by the engine:
W1 rev=2πτ
For the Indirect Measurement, the total torque on the second pulley is zero since it is stationary. Thus the torque exerted on it by the engine via the first pulley is equal and opposite to the torque exerted by the weight. Thus, the torque produced by the engine is the same as for the Direct Measurement: r x F. Similarly, Eqns (1) and (2) above give the work done by the engine after one revolution; the energy in this case goes into the heat produced by the friction.
After the engine has made Δn revolutions, the work done is:
WΔn rev=2πτΔn
Thus the rate of work being done, the power, is:
P=2πτ(ΔnΔt)
Typically, the speed of the engine is measured in revolutions per minute (rpm), which is related to revolutions per second by:
ΔnΔt=rpm60
Thus, the power is:
P=2 π τ rpm60
In the British system of units, the units of the power in Eqn (6) are ft-lb/sec. Since 1 horsepower is 550 ft-lb/sec, then, the horsepower of the engine is:
hp=2 π τ rpm60(550)
hp=τ rpm5252
Conclusions
We have seen that the horsepower of an engine is derived from a measurement of its torque. A moment's reflection may convince you that the torque really is the fundamental quantity of interest in measuring the strength of an engine, since it is the torque exerted by the pavement on the wheels that causes the vehicle to accelerate.
You can also see from Eqn. (7b) that at 5252 rpm the horsepower is always numerically equal to the torque. When the rpm is less than 5252 rpm, the horsepower is less than the torque, and when the rpm is greater than 5252 rpm the horsepower is greater than the torque.
The apparatus that measures the output of an engine is called a dynamometer. The following is the result of a "dyno" measurement of a customized 1200 cc V-twin motorcycle engine. The lighter blue curve is the torque, and the dark blue one is the horsepower.
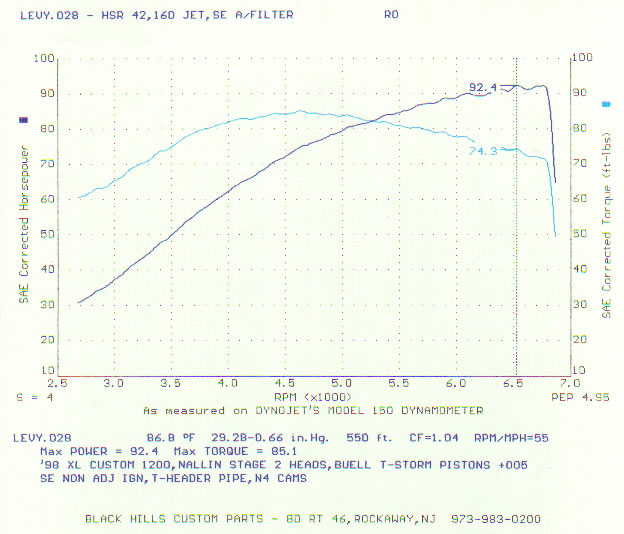
The above graph was made for an engine customized by Moshe K. Levy, and is used by permission. The original site is http://www.mklsportster.com/xlnallinstage2.htm.
Finally, then, for everyday use in a vehicle a good engine delivers high torque and delivers that torque over a wide a range of rpm. The derived value of the horsepower is not nearly as good a measure of the engine.
Question
In the SI system of units, the power of the engine is typically expressed in kilowatts, and the torque in N-m. What is the equivalent of Eqn. (7b) for a dynamometer which measures the torque in SI units and for which we wish to express the power in kW?

