Spectra

Waves

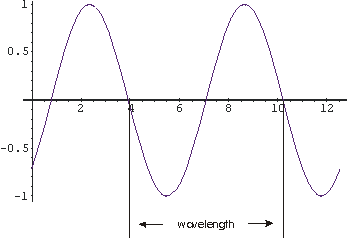As proved by Thomas Young in the early nineteenth century, light is a wave. Later in the century Faraday and Maxwell realized that it is a wave of electric and magnetic fields, and now we often call it electromagnetic radiation. The strength of the fields is called the amplitude of the wave; in the figure to the right the amplitude is one.

The wavelength of the wave is the length from a point on the wave to the point where the oscillation begins to repeat; in the figure it is about 6.3 units.

The wavelength of electromagnetic radiation can range from very small to very large. If the wavelength is between 400 and 700 billionths of a meter, our eyes are sensitive to it and we call it light. The smaller wavelength we see as the color violet; as the wavelength increases the we see color change to blue, green, yellow, orange and red in that order. If the wavelength is out of this range the physical phenomenon is the same but we give it different names such as radio waves, X rays, gamma rays, etc.

To the left we show a wave traveling through space. We also indicate by means of a small circle the amplitude of the wave as it goes by us. The frequency of oscillation of the dot is the frequency of the wave.

The animation is a bit "chunky" to keep its total file size to a reasonable 45k.

Technical note: the frequency of a wave times its wavelength is equal to the speed of the wave.

Spectra

Glasses tend to bend the path of light, a phenomenon called refraction. For many glasses, the amount of bending depends on the wavelength of the light; such glasses are called dispersive. Thus, if we have white light incident on a prism made of a dispersive glass, we break the light into its component colors. Newton was one of the first people to investigate this "phenomenon of the colours."

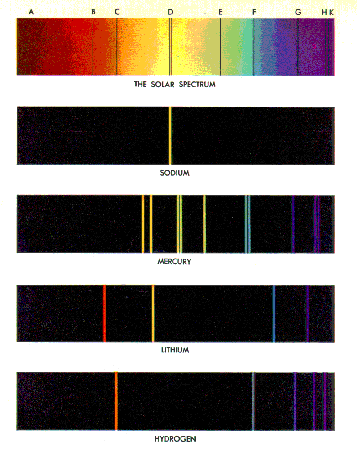If we look more carefully at the spectrum from the Sun, we see that there are some discrete wavelengths that are missing. This is shown to the right, and we will explain it soon.

If we have a trace amount of a pure element and subject it to a strong electric field, it will emit light whose color is characteristic of the particular element. Neon lights are an example of this phenomenon.

Some spectra of pure elements are shown to the right.

Note that for pure elements the spectra consists of discrete wavelengths. In the early 1900's there were attempts to explain these line spectra by analogy to the standing waves of organ pipes. A document on standing waves is available here.

The Sodium spectrum looks like a single wavelength, but is actually two nearly identical wavelengths.

Note that there is some hint of a pattern in the wavelengths for the Hydrogen spectrum.

The spectrum of each pure element is unique, and in the late nineteenth century the values of the line spectra for many elements were well known.

In the 1880's there was a German schoolteacher named Balmer whose hobby was numerology. He was into trying to find significance in prime factors of the number of steps of the great pyramid and things like that. He had a friend who was a chemist, who suggested that he have a bash at the Hydrogen spectrum. Through trial and error he came up with a simple formula. For completeness, here is is:

\[\frac{1}{wavelength}=R\left(\frac{1}{2^2} -\frac{1}{n^2}\right)\]

Here R is a constant equal to about 10,970,000 and n is any integer greater than 2, such as 3, 4, 5, 108, etc.. Each different value of n gives the wavelength of a different line in the Hydrogen spectrum.

Finally, we end by discussing the missing lines in the solar spectrum. The wavelength of one of the lines in a pure element spectrum is fixed provided the element is stationary relative to us. If it is moving, say, towards us the Doppler effect will decrease its wavelength and increase its frequency; if it is moving away the wavelength increases and the frequency decreases. This is true for all waves, and you have probably noticed the effect when a car playing loud music passes by you. For the elements in the gas lamps whose spectra we showed above, the Doppler effect turns out to be negligible.

However, the temperature of the interior of the Sun is so high that the atoms are vibrating very fast. The Doppler effect strongly smears out the wavelengths of the lines from all the elements that are emitting the light. Thus, the spectrum emitted by the interior of the Sun is continuous, not a large collection of discrete wavelengths.

If an element has a particular spectrum, then the wavelengths of that spectrum are also the wavelengths that the element can absorb from an incident light beam. The outer mantle of the Sun is relatively cool, and the elements in that mantle absorb wavelengths of the light from the interior corresponding to their own light spectra. Thus, you can see that missing from the solar spectrum are the lines corresponding to Sodium. From this we know that Sodium is present in the outer mantle of the Sun.

In fact, the element Helium was first discovered by analyzing missing lines in the spectrum of the Sun.