4.4: Newton's Third Law
- Page ID
- 101215
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
The image above is a NASA artist’s conceptual illustration of a space elevator. It was imagined as a geo-stationary transfer station for passengers and cargo between Earth and space. This idea was not pursued beyond the initial discussion and evaluation stage, but the scientists involved believe the concept will become truly possible with the expected technological advances of the late 21st century.
Newton’s Third Law of Motion
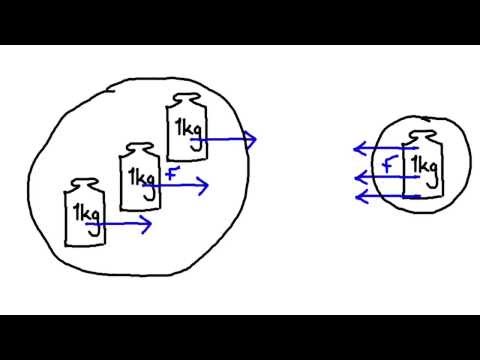
Where do forces come from? Observations suggest that a force applied to an object is always applied by another object. A hammer strikes a nail, a car pulls a trailer, and a person pushes a grocery cart. Newton realized that forces are not so one-sided. When the hammer exerts a force on the nail, the nail also exerts a force on the hammer—after all, the hammer comes to rest after the interaction. This led to Newton’s Third Law of Motion, which states that whenever one object exerts a force on a second object, the second object also exerts a force on the first object, equal in magnitude and opposite in direction.
This law is sometimes paraphrased as: “For every action, there is an equal and opposite reaction.” A very important point to remember is that the two forces are on different objects—never on the same object. It is frequently the case that one of the objects moves as a result of the force applied but the motion of the other object in the opposite direction is not apparent.
Consider the situation where an ice skater is standing at the edge of the skating rink holding on to the side rail. If the skater exerts a force on the rail, the rail is held in place with tremendous friction and therefore, will not move in any noticeable way. The skater, on the other hand, had little friction with the ice, and therefore will be accelerated in the direction opposite of her original push. This is the process people use to jump up into the air. The person's feet exert force on the ground and the ground exerts an equal and opposite force on the person's feet. The force on the feet is sufficient to raise the person off the ground. The force on the ground has little effect because the Earth is so large. One of the accelerations is visible but the other is not visible.
A case where the reaction motion due to the reaction force is visible is the case of a person throwing a heavy object out of a small boat, such as a kayak. The object is accelerated in one direction and the boat is accelerated in the opposite direction. In this case, both the motion of the object is visible and the motion of the boat in the opposite direction is also visible. Explore the resulting motion of two interacting objects as a result of Newton’s Third Law in this Pirate Ship simulation below:
Rockets also work in this manner. It is a misconception that the rocket moves forward because the escaping gas pushes on the ground or the surrounding air to make the rocket go forward. Rockets work in outer space where there is no ground or surrounding air. The rocket exerts a force on the gases causing them to be expelled and the gases exert a force on the rocket causing it to be accelerated forward.
The applications of Newton’s Third Law can also be explored in the classic example if a horse pulling a cart. How does the horse-cart system move if the cart pulls on the horse with the same exact force and in the opposite direction as the horse pulls on the cart? (Beware, there are many misconceptions related to this example! Always remember that Newton’s Third Law applies to the same type of force acting on different objects).
Summary
- A force applied to an object is always applied by another object.
- Newton’s Third Law of Motion states, “Whenever one object exerts a force on a second object, the second object also exerts a force on the first object, equal in magnitude and opposite in direction.”
Review
- What is wrong with the following statement: When you exert a force on a baseball, the equal and opposite force on the ball balances the original force and therefore, the ball will not accelerate in any direction.
- When a bat strikes a ball, the force exerted can send the ball deep into the outfield. Where is the equal and opposite force in this case?
- Suppose you wish to jump horizontally and in order for you to jump a distance of 4 feet horizontally, you must exert a force of 200 N. When you are standing on the ground, you have no trouble jumping 4 feet horizontally. If you are standing in a canoe, however, and you need to jump 4 feet to reach the pier, you will surely fall into the lake. Why is it that you cannot jump 4 feet out of a canoe when you can easily do this when on land?
Explore More
Use the resource below to answer the questions that follow.
- What does the bottle rocket have to do with Newton’s Third Law of Motion?
Additional Resources
PLIX: Play, Learn, Interact, eXplore: Rocket Science, Newton's 3rd Law: Gravity of Neptune
Real World Application: Rebuilding the Bridge
Video:
Study Guide: Newton's Laws Study Guide