2.5: Conic Sections
( \newcommand{\kernel}{\mathrm{null}\,}\)
We have so far defined an ellipse, a parabola and a hyperbola without any reference to a cone. Many readers will know that a plane section of a cone is either an ellipse, a parabola or a hyperbola, depending on whether the angle that the plane makes with the base of the cone is less than, equal to or greater than the angle that the generator of the cone makes with its base. However, given the definitions of the ellipse, parabola and hyperbola that we have given, proof is required that they are in fact conic sections. It might also be mentioned at this point that a plane section of a circular cylinder is also an ellipse. Also, of course, if the plane is parallel with the base of the cone, or perpendicular to the axis of the cylinder, the ellipse reduces to a circle.
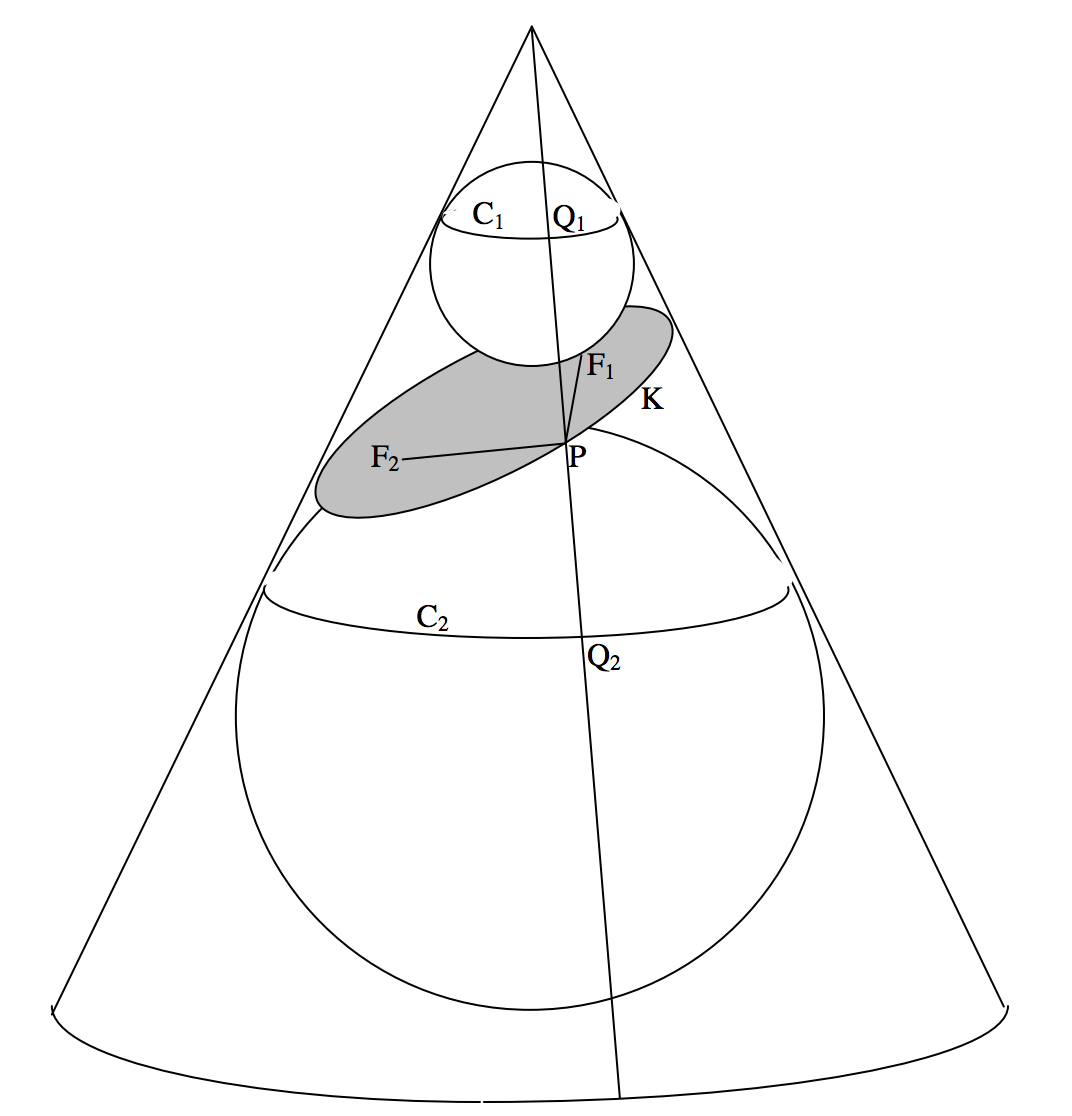
FIGURE II.36
A simple and remarkable proof can be given in the classical Euclidean "Given. Required. Construction. Proof. Q.E.D." style.
Given: A cone and a plane such that the angle that the plane makes with the base of the cone is less than the angle that the generator of the cone makes with its base, and the plane cuts the cone in a closed curve K. Figure II.36.
Required: To prove that K is an ellipse.
Construction: Construct a sphere above the plane, which touches the cone internally in the circle C1 and the plane at the point F1. Construct also a sphere below the plane, which touches the cone internally in the circle C2 and the plane at the point F2.
Join a point P on the curve K to F1 and to F2.
Draw the generator that passes through the point P and which intersects C1 at Q1 and C2 at Q2.
Proof: PF1=PQ1 (Tangents to a sphere from an external point.)
PF2=PQ2 (Tangents to a sphere from an external point.)
∴PF1+PF2=PQ1+PQ2=Q1Q2
and Q1Q2 is independent of the position of P, since it is the distance between the circles C1 and C2 measured along a generator.
∴ K is an ellipse and F1 and F2 are its foci.
A similar argument will show that a plane section of a cylinder is also an ellipse.
The reader can also devise drawings that will show that a plane section of a cone parallel to a generator is a parabola, and that a plane steeper than a generator cuts the cone in a hyperbola. The drawings are easiest to do with paper, pencil, compass and ruler, and will require some ingenuity. While I have seen the above proof for an ellipse in several books, I have not seen the corresponding proofs for a parabola and a hyperbola, but they can indeed be done, and the reader should find it an interesting challenge. If the reader can use a computer to make the drawings and can do better than my poor effort with figure II.36, s/he is pretty good with a computer, which is a sign of a misspent youth.


