2.6: The General Conic Section

The Equation \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.7.1} \tag{2.7.1}\]

represents an ellipse whose major axis is along the \(x\) axis and whose centre is at the origin of coordinates. But what if its centre is not at the origin, and if the major axis is at some skew angle to the \(x\) axis? What will be the Equation that represents such an ellipse? Figure \(\text{II.37}\).

\(\text{FIGURE II.37}\)

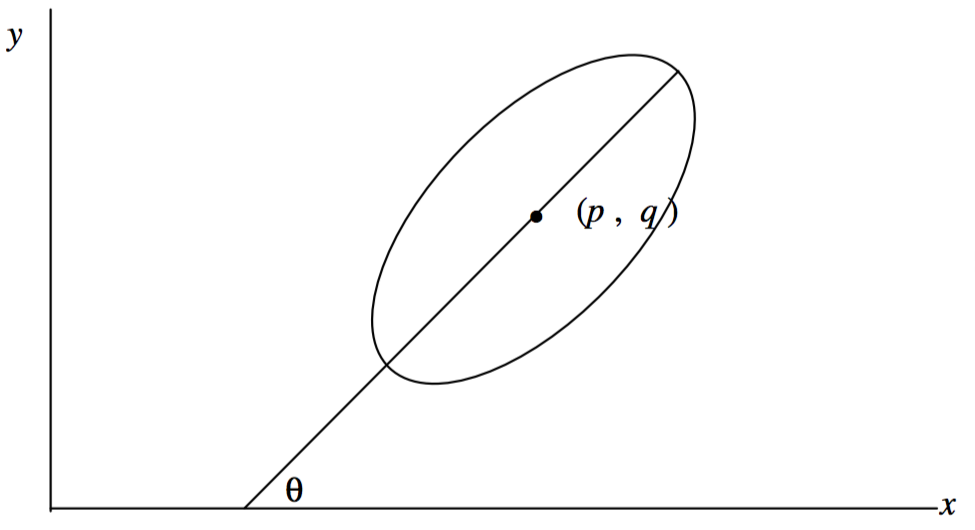
If the centre is translated from the origin to the point \((p, q)\), the Equation that represents the ellipse will be found by replacing \(x\) by \(x − p\) and \(y\) by \(y − q\). If the major axis is inclined at an angle θ to the \(x\) axis, the Equation that represents the ellipse will be found by replacing \(x\) by \(x \cos θ + y \sin θ\) and \(y\) by \(−x \sin θ + y \cos θ\). In any case, if the ellipse is translated or rotated or both, \(x\) and \(y\) will each be replaced by linear expressions in \(x\) and \(y\), and the resulting Equation will have at most terms in \(x^2 , \ y^2 , \ xy, \ x, \ y\) and a constant. The same is true of a parabola or a hyperbola. Thus, any of these three curves will be represented by an Equation of the form

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0. \label{2.7.2} \tag{2.7.2}\]

(The coefficients \(a\) and \(b\) are not the semi major and semi minor axes.) The apparently random notation for the coefficients arises because these figures are plane sections of three-dimensional surfaces (the ellipsoid, paraboloid and hyperboloid) which are described by terms involving the coordinate \(z\) as well as \(x\) and \(y\). The customary notation for these three-dimensional surfaces is very systematic, but when the terms in \(z\) are removed for the two- dimensional case, the apparently random notation \(a, \ b, \ c, \ f, \ g, \ h\) remains. In any case, the above Equation can be divided through by the constant term without loss of generality, so that the Equation to an ellipse, parabola or hyperbola can be written, if preferred, as

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0. \label{2.7.3} \tag{2.7.3}\]

Is the converse true? That is, does an Equation of this form always necessarily represent an ellipse, parabola or hyperbola?

Not quite. For example,

\[6x^2 + xy - y^2 - 17x - y + 12 = 0 \label{2.7.4} \tag{2.7.4}\]

represents two straight lines (it can be factored into two linear terms - try it), while

\[2x^2 -4xy + 4y^2 -4x + 4 = 0 \label{2.7.5} \tag{2.7.5}\]

is satisfied only by a single point. (Find it.)

However, a plane section of a cone can be two lines or a single point, so perhaps we can now ask whether the general second degree Equation must always represent a conic section. The answer is: close, but not quite.

For example,

\[4x^2 + 12xy + 9y^2 + 14x + 21y + 6 = 0 \label{2.7.6} \tag{2.7.6}\]

represents two parallel straight lines, while

\[x^2 + y^2 + 3x + 4y + 15 = 0 \label{2.7.7} \tag{2.7.7}\]

cannot be satisfied by any real \((x,y)\).

However, a plane can intersect a cylinder in two parallel straight lines, or a single straight line, or not at all. Therefore, if we stretch the definition of a cone somewhat to include a cylinder as a special limiting case, then we can say that the general second degree Equation in \(x\) and \(y\) does indeed always represent a conic section.

Is there any means by which one can tell by a glance at a particular second degree Equation, for example

\[8x^2 + 10xy -3y^2 -2x - 4y - 2 = 0, \label{2.7.8} \tag{2.7.8}\]

what type of conic section is represented? The answer is yes, and this one happens to be a hyperbola. The discrimination is made by examining the properties of the determinant

\begin{array}{l | c c c |}
& a & h & g \\
\Delta = & h & b & f \\
& g & f & c \\
\label{2.7.9} \tag{2.7.9}
\end{array}

I have devised a table after the design of the dichotomous tables commonly used by taxonomists in biology, in which the user is confronted by a couplet (or sometimes triplet) of alternatives, and is then directed to the next part of the table. I shall spare the reader the derivation of the table; instead, I shall describe its use.

In the table, I have used the symbol \(\bar{a}\) to mean the cofactor of \(a\) in the determinant, \(\bar{h}\) the cofactor of \(h\), \(\bar{g}\) the cofactor of \(g\), etc. Explicitly, these are

\[\bar{a} = bc - f^2 , \label{2.7.10} \tag{2.7.10}\]
\[\bar{b} = ca - g^2 , \label{2.7.11} \tag{2.7.11}\]
\[\bar{c} = ab - h^2 , \label{2.7.12} \tag{2.7.12}\]
\[\bar{f} = gh - af , \label{2.7.13} \tag{2.7.13}\]
\[\bar{g} = hf - bg \label{2.7.14} \tag{2.7.14}\]
and \[\bar{h} = fg - ch . \label{2.7.15} \tag{2.7.15}\]

The first column labels the choices that the user is asked to make. At the beginning, there are two choices to make, \(1\) and \(1^\prime\) The second column says what these choices are, and the fourth column says where to go next. Thus, if the determinant is zero, go to \(2\); otherwise, go to \(5\). If there is an asterisk in column \(4\), you are finished. Column \(3\) says what sort of a conic section you have arrived at, and column \(5\) gives an example.

No matter what type the conic section is, the coordinates of its centre are \((\bar{g}/\bar{c}, \ \bar{f}/\bar{c} )\) and the angle \(θ\) that its major or transverse axis makes with the x axis is given by

\[\tan 2θ = \frac{2h}{a-b}. \label{2.7.16} \tag{2.7.16}\]

Thus if \(x\) is first replaced with \(x + \bar{g} / \bar{c}\) and \(y\) with \(y + \bar{f}/\bar{c}\), and then the new \(x\) is replaced with \(x \cos θ − y \sin θ\) and the new \(y\) with \(x \sin θ + y \cos θ\), the Equation will take the familiar form of a conic section with its major or transverse axis coincident with the \(x\) axis and its centre at the origin. Any of its properties, such as the eccentricity, can then be deduced from the familiar Equations. You should try this with Equation \(\ref{2.7.8}\).

Key to the Conic Sections

When faced with a general second degree Equation in \(x\) and \(y\), I often find it convenient right at the start to calculate the values of the cofactors from Equations 2.7.10 − 2.7.15.

Here is an exercise that you might like to try. Show that the ellipse \(ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0\) is contained within the rectangle whose sides are

\[x = \frac{\bar{g} \pm \sqrt{\bar{g}^2 - \bar{a} \bar{c}}}{\bar{c}} \label{2.7.18} \tag{2.7.18}\]

\[y = \frac{\bar{f} \pm \sqrt{\bar{f}^2 - \bar{b} \bar{c}}}{\bar{c}} \label{2.7.19} \tag{2.7.19}\]

In other words, these four lines are the vertical and horizontal tangents to the ellipse.

This is probably not of much use in celestial mechanics, but it will probably be useful in studying Lissajous ellipses, or the Stokes parameters of polarized light. It is also useful in programming a computer to draw, for example, the ellipse \(14x^2 - 4xy + 11y^2 - 44x -58y + 71 = 0\). To do this, you will probably want to start at some value of \(x\) and calculate the two corresponding values of \(y\), and then move to another value of \(x\). But at which value of \(x\) should you start? Equation \(\ref{2.7.18}\) will tell you.

But what do Equations \(\ref{2.7.18}\) and \(\ref{2.7.19}\) mean if the conic section Equation \(ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0\) is not an ellipse? They are still useful if the conic section is a hyperbola. Equations \(\ref{2.7.18}\) and \(\ref{2.7.19}\) are still vertical and horizontal tangents - but in this case the hyperbola is entirely outside the limits imposed by these tangents. If the axes of the hyperbola are horizontal and vertical, one or other of Equations \(\ref{2.7.18}\) and \(\ref{2.7.19}\) will fail.

If the conic section is a parabola, Equations \(\ref{2.7.18}\) and \(\ref{2.7.19}\) are not useful, because \(c = 0\). There is only one horizontal tangent and only one vertical tangent. They are given by

\[x = \frac{\bar{a}}{2\bar{g}} \label{2.7.20} \tag{2.7.20}\]

and \[y = \frac{\bar{b}}{2\bar{f}} \tag{2.7.21} \label{2.7.21}\]

If the axis of the parabola is horizontal or vertical, one or other of Equations \(\ref{2.7.20}\) and \(\ref{2.7.21}\) will fail.

If the second degree Equation represents one or two straight lines, or a point, or nothing, I imagine that all of Equations \(\ref{2.7.18}\) − \(\ref{2.7.21}\) will fail - unless perhaps the Equation represents horizontal or vertical lines. I haven’t looked into this; perhaps the reader would like to do so.

Here is a problem that you might like to try. The Equation \(8x^2 + 10xy - 3y^2 - 2x - 4y - 2 = 0\) represents a hyperbola. What are the Equations to its axes, to its asymptotes, and to its conjugate hyperbola? Or, more generally, if \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) represents a hyperbola, what are the Equations to its axes, to its asymptotes, and to its conjugate hyperbola?

Before starting, one point worth noting is that the original hyperbola, its asymptotes, and the conjugate hyperbola) have the same centre, which means that \(g\) and \(f\) are the same for each, and they have the same axes, which means that \(a\), \(h\), and \(b\) are the same for each. They differ only in the constant term.

If you do the first problem, \(8x^2 + 10xy - 3y^2 - 2x - 4y -2 = 0\), there will be a fair amount of numerical work to do. When I did it I didn’t use either pencil and paper or a hand calculator. Rather I sat in front of a computer doing the numerical calculations with a Fortran statement for every stage of the calculation. I don’t think I could have done it otherwise without making lots of mistakes. The very first thing I did was to work out the cofactors \(\bar{a}, \ \bar{h}, \ \bar{b}, \ \bar{g}, \ \bar{f}, \ \bar{c}\) and store them in the computer, and also the coordinates of the centre \((x_0, y_0)\) of the hyperbola, which are given by \(x_0 = \bar{g}/\bar{c}, \ y_0 = \bar{f} / \bar{c}\).

Whether you do the particular numerical problem, or the more general algebraic one, I suggest that you proceed as follows. First, refer the hyperbola to a set of coordinates \(x^\prime , y^\prime\) whose origin coincides with the axes of the hyperbola. This is done by replacing \(x\) with \(x^\prime + x_0\) and \(y\) with \(y' + y_0\). This will result in an Equation of the form \(ax^{\prime 2} + 2hx^\prime y^\prime + by^{\prime 2} + c^\prime = 0\). The coefficients of the quadratic terms will be unchanged, the linear terms will have vanished, and the constant term will have changed. At this stage I got, for the numerical example, \(8x^{\prime 2} + 10x^\prime y^\prime - 3y^{\prime 2} - 1.8163 = 0\).

Now refer the hyperbola to a set of coordinates \(x^{\prime \prime}, y^{\prime \prime}\) whose axes are parallel to the axes of the hyperbola. This is achieved by replacing \(x^\prime\) with \(x^{\prime \prime} \cos θ − y^{\prime \prime} \sin θ\) and \(y^\prime\) with \(x^{\prime \prime} \sin θ + y^{\prime \prime} \cos θ\), where \(\tan 2θ = 2h /(a − b)\). There will be a small problem here, because this gives two values of \(θ\) differing by \(90^\circ\), and you’ll want to decide which one you want. In any case, the result will be an Equation of the form \(a^{\prime \prime} x^{\prime \prime 2} + b^{\prime \prime} y^{\prime \prime 2} + c^\prime = 0\), in which \(a^{\prime \prime}\) and \(b^{\prime \prime}\) are of opposite sign. Furthermore, if you happen to understand the meaning of the noise “The trace of a matrix is invariant under an orthogonal transformation”, you’ll be able to check for arithmetic mistakes by noting that \(a^{\prime \prime} + b^{\prime \prime} = a + b\). If this is not so, you have made a mistake. Also, the constant term should be unaltered by the rotation (note the single prime on the \(c\)). At this stage, I got \( 9.933 x^{\prime \prime 2} - 4.933y^{\prime \prime 2} - 1.8163 = 0\). (All of this was done with Fortran statements on the computer - no actual calculation or writing done by me - and the numbers were stored in the computer to many significant figures).

In any case this Equation can be written in the familiar form \(\dfrac{x^{\prime \prime 2}}{A^2}-\dfrac{y^{\prime \prime 2}}{B^2}=1\), which in this case I made to be \(\dfrac{x^{\prime \prime 2}}{0.4283^2}-\dfrac{y^{\prime \prime 2}}{0.6088^2}=1\). We are now on familiar ground. The axes of the hyperbola are \( x^{\prime \prime} = 0\) and \(y^{\prime \prime} = 0\), the asymptotes are \(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = 0\) and the conjugate hyperbola is \(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = -1\).

Now, starting from \(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = -1\) for the asymptotes, or from \(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} =-1\) for the conjugate hyperbola, we reverse the process. We go to the single-primed coordinates by replacing \(x^{\prime \prime}\) with \(x^\prime \cos θ + y^\prime \sin θ\) and \(y^{\prime \prime}\) with − \(x^\prime \sin θ + y' \cos θ\), and then to the original coordinates by replacing \(x^\prime\) with \(x − x_0\) and \(y^\prime\) with \(y − y_0\).

This is what I find:

Original hyperbola: \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\)

Conjugate hyperbola: \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{conj}} = 0,\)
where \(c_{\text{conj}} = -(2g \bar{g} + 2f \bar{f} + c \bar{c})/ \bar{c} = -(2gx_0 + 2fy_0 + c).\)

Asymptotes: \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{asymp}} = 0,\)
where \(c_{\text{asymp}}\) can be written in any of the following equivalent forms:
\[c_{\text{asymp}} = + (a \bar{g}^2 + 2h \bar{g} \bar{f} + b \bar{f}^2 ) / \bar{c}^2 = ax_0^2 + 2hx_0 y_0 + by_0^2 = -(g \bar{g} + f \bar{f}) / \bar{c} .\]
[The last of these three forms can be derived very quickly by recalling that a condition for a general second degree Equation in \(x\) and \(y\) to represent two straight lines is that the determinant \(∆\) should be zero. A glance at this determinant will show that this implies that \(g\bar{g} + f\bar{f} + c\bar{c} = 0.\) ]

Axes of hyperbolas: \((y - x \tan θ - y_0 + x_0 \tan θ) ( y + x \cot θ - y_0 - x_0 \cot θ) = 0,\)
where \( \tan 2 θ = 2h / (a-b) . \)

Example:

Original hyperbola: \(8x^2 + 10xy - 3y^2 - 2x - 4y - 2 = 0\)

Conjugate hyperbola: \(8x^2 + 10xy - 3y^2 - 2x - 4y + \frac{80}{49} = 0\)

Asymptotes: \(8x^2 + 10xy - 3y^2 - 2x -4y - \frac{9}{49} = 0 , \)
which can also be written \((4x - y - \frac{9}{7})(2x + 3y + \frac{1}{7}) = 0\)

Axes of hyperbolas: \(( y − 0.3866x + 0.3275)( y + 2.5866 x − 0.4613)\).

These are shown in the figure below - the original hyperbola in black, the conjugate in blue.

The centre is at (0.26531, −0.22449).

The slopes of the two asymptotes are 4 and \(−\frac{2}{3}\). From Equation 2.2.16 we find that the tangent of the angle between the asymptotes is \(\tan 2ψ = \frac{14}{5}\), so that \(2ψ = 70^\circ .3\), and the angle between the asymptote and the major axis of the original hyperbola is \(54^\circ .8\), or \(\tan ψ = 1.419\). This is equal (see Equations 2.5.3 and 2.5.10) to \(\sqrt{e^2 - 1}\), so the eccentricity of the original hyperbola is \(1.735\). From Section 2.2, shortly Equation 2,5,6, we soon find that the eccentricity of the conjugate hyperbola is \(\csc ψ = 1.223\).

An interesting question occurs to me. We have found that, if \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) is a hyperbola, then the Equations to the conjugate hyperbola and the asymptotes are of a similar form, namely \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{conj}} = 0\) and \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{asymp}} = 0\), and we found expressions for \(c_{\text{conj}}\) and \(c_\text{asymp}\). But what if \(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) is not a hyperbola? What if it is an ellipse? What do the other Equations represent, given that an ellipse has neither a conjugate nor asymptotes?

For example, \(14x^2 - 4xy + 11y^2 - 44x -58y + 71 = 0\) is an ellipse. What are \(14x^2 - 4xy + 11y^2 - 44x - 58y + 191 = 0\) and \(14x^2 -4xy + 11y^2 - 44x - 58y + 131 = 0\)? I used the key on page 47, and it told me that the first of these Equations is satisfied by no real points, which I suppose is the Equation’s way of telling me that there is no such thing as the conjugate to an ellipse. The second Equation was supposed to be the “asymptotes”, but the key shows me that the Equation is satisfied by just one real point, namely (2 , 3), which coincides with the centre of the original ellipse. I didn’t expect that. Should I have done so?