14.1: Preliminaries- Conic Sections

Last updated
Save as PDF

Page ID: 29484

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

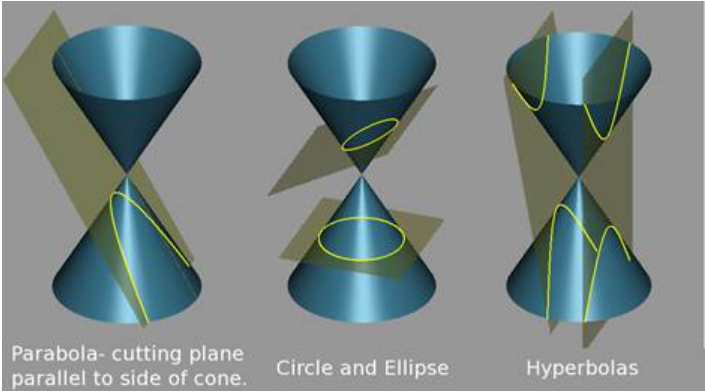
Ellipses, parabolas and hyperbolas can all be generated by cutting a cone with a plane (see diagrams, from Wikimedia Commons). Taking the cone to be \(x^{2}+y^{2}=z^{2}\), and substituting the z in that equation from the planar equation \(\vec{r} \cdot \vec{p}=p, \text { where } \vec{p}\) is the vector perpendicular to the plane from the origin to the plane, gives a quadratic equation in \(x,y\). This translates into a quadratic equation in the plane—take the line of intersection of the cutting plane with the \(x,y\) plane as the \(y\) axis in both, then one is related to the other by a scaling \(x^{\prime}=\lambda x\). To identify the conic, diagonalized the form, and look at the coefficients of \(x^{2}, y^{2}\). If they are the same sign, it is an ellipse, opposite, a hyperbola. The parabola is the exceptional case where one is zero, the other equates to a linear term. It is instructive to see how an important property of the ellipse follows immediately from this construction.

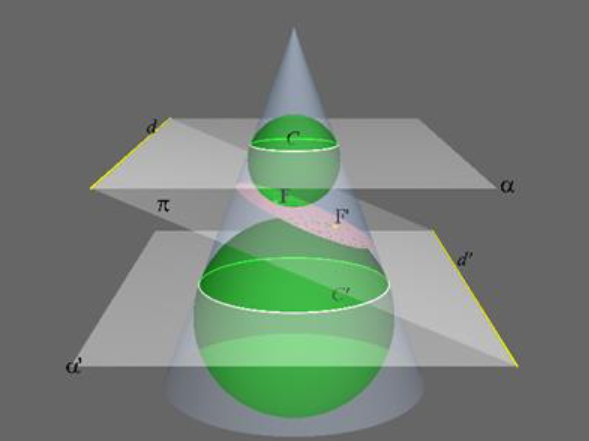
The slanting plane in the figure cuts the cone in an ellipse. Two spheres inside the cone, having circles of contact with the cone \(C, C^{\prime}\), are adjusted in size so that they both just touch the plane, at points \(F, F^{\prime}\) respectively.

It is easy to see that such spheres exist, for example start with a tiny sphere inside the cone near the point, and gradually inflate it, keeping it spherical and touching the cone, until it touches the plane. Now consider a point \(P\) on the ellipse. Draw two lines: one from \(P\) to the point \(F\) where the small sphere touches, the other up the cone, aiming for the vertex, but stopping at the point of intersection with the circle \(C\). Both these lines are tangents to the small sphere, and so have the same length. (The tangents to a sphere from a point outside it form a cone, they are all of equal length.) Now repeat with \(F^{\prime}, C^{\prime}\). We find that \(P F+P F^{\prime}=P C+P C^{\prime}\), the distances to the circles measured along the line through the vertex. So \(P F+P F^{\prime}=C C^{\prime} \text { in the obvious notation }-F, F^{\prime}\) are therefore evidently the foci of the ellipse.