3.6: Rotation of Axes, Two Dimensions
( \newcommand{\kernel}{\mathrm{null}\,}\)
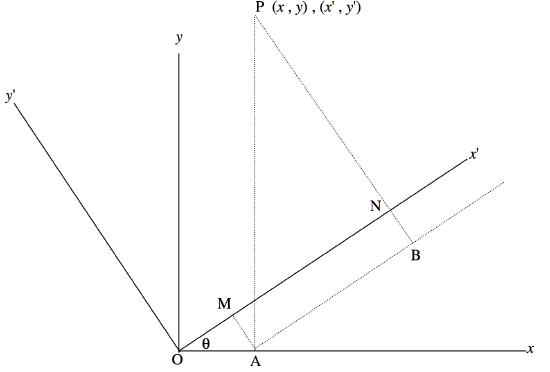
In this section we consider the following problem. Consider two sets of orthogonal axes, Ox,Oy, and Ox′,Oy′, such that one set makes an angle θ with respect to the other. See figure (a) below. A point P can be described either by its coordinates (x,y) with respect to one "basis set" Ox,Oy, or by its coordinates with respect to the other basis set Ox′,Oy′. The question is, what is the relation between the coordinates (x,y) and the coordinates (x′,y′)? See figure III.18.
We see that OA=x, AP=y, ON=x′, PN=y′, OM=xcosθ, MN=ysinθ,
∴
Also \text{MA} = \text{NB} = x \sin θ, \quad \text{PB} = y \cos θ,
\therefore \quad y^\prime = -x \sin θ + y \cos θ. \label{3.6.2} \tag{3.6.2}
These two relations can be written in matrix form as
\pmatrix{x^\prime \\ y^\prime} = \pmatrix{\cos θ & \sin θ \\ -\sin θ & \cos θ} \pmatrix{x \\ y}. \label{3.6.3} \tag{3.6.3}
\text{FIGURE III.18}
There are several ways of obtaining the converse relations; that is, Equations for x and y in terms of x^\prime and y^\prime. One way would be to design drawings similar to (b) and (c) that show the converse relations clearly, and the reader is encouraged to do this. Another way is merely to solve the above two Equations (which can be regarded as two simultaneous Equations in x and y) for x and y. Less tedious is to interchange the primed and unprimed symbols and change the sign of θ. Perhaps the quickest of all is to recognize that the determinant of the matrix
\pmatrix{\cos θ & \sin θ \\ -\sin θ & \cos θ}
is unity and therefore the matrix is an orthogonal matrix. One important property of an orthogonal matrix M is that its reciprocal M^{−1} is equal to its transpose \tilde{\textbf{M}} (formed by transposing the rows and columns). Therefore the converse relation that we seek is
\pmatrix{x \\ y} = \pmatrix{\cos θ & \sin θ \\ - \sin θ & \cos θ}^{-1} \pmatrix{x^\prime \\ y^\prime} = \pmatrix{\cos θ & -\sin θ \\ \sin θ & \cos θ} \pmatrix{x^\prime \\ y^\prime}. \label{3.6.4} \tag{3.6.4}
The reader might like to try all four methods to ensure that they all arrive at the same result.


