3.3: Cylindrical and Spherical Coordinates
- Page ID
- 6800
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
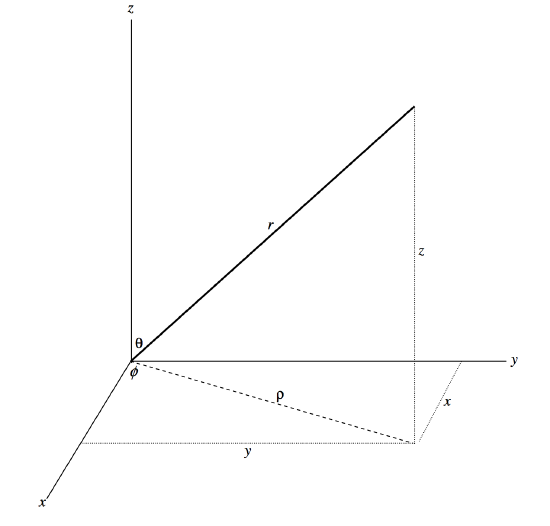
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is assumed that the reader is at least somewhat familiar with cylindrical coordinates \((ρ, \phi, z)\) and spherical coordinates \((r, θ, \phi)\) in three dimensions, and I offer only a brief summary here. Figure \(\text{III.5}\) illustrates the following relations between them and the rectangular coordinates \((x, y, z)\).
\[\begin{align} x &= ρ \cos \phi = r \sin θ \cos \phi \label{3.3.1} \\[8pt] y &= ρ \sin \phi = r \sin θ \sin \phi \label{3.3.2} \\[8pt] z &= r \cos θ \label{3.3.3} \end{align}\]
\(\text{FIGURE III.5}\)
The inverse relations between spherical and rectangular coordinates are
\[r = \sqrt{x^2 + y^2 + z^2} \label{3.3.4} \tag{3.3.4}\]
\[θ = \cos^{-1} \frac{z}{\sqrt{x^2 + y^2 + z^2}} \tag{3.3.5} \label{3.3.5}\]
\[\phi = \cos^{-1} \frac{x}{\sqrt{x^2 + y^2}} = \sin^{-1} \frac{y}{\sqrt{x^2 + y^2}} \label{3.3.6} \tag{3.3.6}\]
The coordinates \(r\), \(θ\) and \(\phi\) are called, respectively, the "radial", "polar" or "meridional", and "azimuthal" coordinates respectively.
Note that \(r\) is essentially positive (the symbol √ denotes the positive or absolute value of the square root). The angle \(θ\) is necessarily between \(0^\circ\) and \(180^\circ\) and therefore there is no quadrant ambiguity in the evaluation of \(θ\). The angle \(\phi\), however, can be between \(0^\circ\) and \(360^\circ\). Therefore, in order to determine \(\phi\) uniquely, both of the above formulas for \(\phi\) must be evaluated, or the signs of \(x\) and \(y\) must be inspected. It does not suffice to calculate \(\phi\) from \(\phi = \tan^{-1} (y/x)\) alone. The reader, however, should be aware that some computer languages and some hand calculator functions will inspect the signs of \(x\) and \(y\) for you and will return \(\phi\) in its correct quadrant. For example, in \(\text{FORTRAN}\), the function \(\text{ATAN2(X,Y)}\) (or \(\text{DATAN2(X,Y)}\) in double precision) will return \(\phi\) uniquely in its correct quadrant (though perhaps as a negative angle, in which case \(360^\circ\) should be added to the outputted angle) provided the arguments \(\text{X}\) and \(\text{Y}\) are inputted with their correct signs. This can save an immense amount of trouble in programming, and the reader should become familiar with this function.
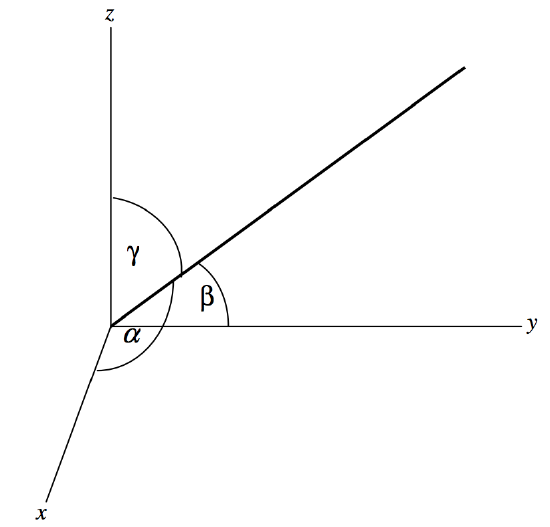
Direction Cosines
The direction to a point in three dimensional space relative to the origin can be described, as we have seen, by the two angles \(θ\) and \(\phi\). Another way of describing the direction to a point, or the orientation of a vector, is to give the angles \(α, \ β, \ γ\) that the vector makes with the \(x\)-, \(y\)- and \(z\)-axes, respectively (see figure \(\text{III.5}\)). The angle \(γ\) is the same as the angle \(θ\).
\(\text{FIGURE III.6}\)
More commonly one quotes the cosines of these three angles. These are called the direction cosines, and are often denoted by \((l,m,n)\). It should not take long for the reader to be convinced that the relation between the direction cosines and the angles \(θ\) and \(\phi\) are
\[l = \cos α = \sin θ \cos \phi \label{3.3.7} \tag{3.3.7}\]
\[m = \cos β = \sin θ \sin \phi \label{3.3.8} \tag{3.3.8}\]
\[n = \cos γ = \cos θ \label{3.3.9} \tag{3.3.9}\]
These are not independent, and are related by
\[l^2 + m^2 + n^2 = 1. \label{3.3.10} \tag{3.3.10}\]
A set of numbers that are multiples of the direction cosines - i.e. are proportional to them - are called direction ratios.
Latitude and Longitude
The figure of the Earth is not perfectly spherical, for it is slightly flattened at the poles. For the present, however, our aim is to become familiar with spherical coordinates and with the geometry of the sphere, so we shall suppose the Earth to be spherical. In that case, the position of any town on Earth can be expressed by two coordinates, the latitude \(\phi\), measured north or south of the equator, and the longitude \(λ\), measured eastwards or westwards from the meridian through Greenwich. These symbols, \(\phi\) for latitude and \(λ\) for longitude, are unfortunate, but are often used in this context. In terms of the symbols \(θ\), \(\phi\) for spherical coordinates that we have used hitherto, the east longitude would correspond to \(\phi\) and the latitude to \(90^\circ − θ\).
A plane that intersects a sphere does so in a circle. If that plane passes through the centre of the sphere (so that the centre of the circle is also the centre of the sphere), the circle is called a great circle. All the meridians (the circles of fixed longitude that pass through the north and south poles) including the one that passes through Greenwich, are great circles, and so is the equator. Planes that do not pass through the centre of the sphere (such as parallels of latitude) are small circles. The radius of a parallel of latitude is equal to the radius of the sphere times the cosine of the latitude.
We have used the example of latitude and longitude on a spherical Earth in order to illustrate the concepts of great and small circles. Although it is not essential to pursue it in the present context, we mention in passing that the true figure of the Earth at mean sea level is a geoid - which merely means the shape of the Earth. To a good approximation, the geoid is an oblate spheroid (i.e. an ellipse rotated about its minor axis) with semi major axis \(a = 6378.140 \ \text{km}\) and semi minor axis \(c = 6356.755 \text{ km}\). The ratio \((a−c)/a\) is called the geometric ellipticity of the Earth and it has the value \(1/298.3\). The mean radius of the Earth, in the sense of the radius of a sphere having the same volume as the actual geoid, is a \(\sqrt[3]{a^2 c} = 6371.00 \text{ km}\).
It is necessary in precise geodesy to distinguish between the geographic or geodetic latitude \(\phi\) of a point on the Earth's surface and its geocentric latitude \(\phi^\prime\). Their definitions evident from figure \(\text{III.7}\). In this figure, the ellipticity of the Earth is greatly exaggerated; in reality it would scarcely be discernible. The angle \(\phi\) is the angle between a plumb-bob and the equator. This differs from \(\phi^\prime\) partly because the gravitational field of a spheroid is not the same as that of an equal point mass at the centre, and partly because the plumb bob is pulled away from the Earth's rotation axis by centrifugal force.
\(\text{FIGURE III.7}\)
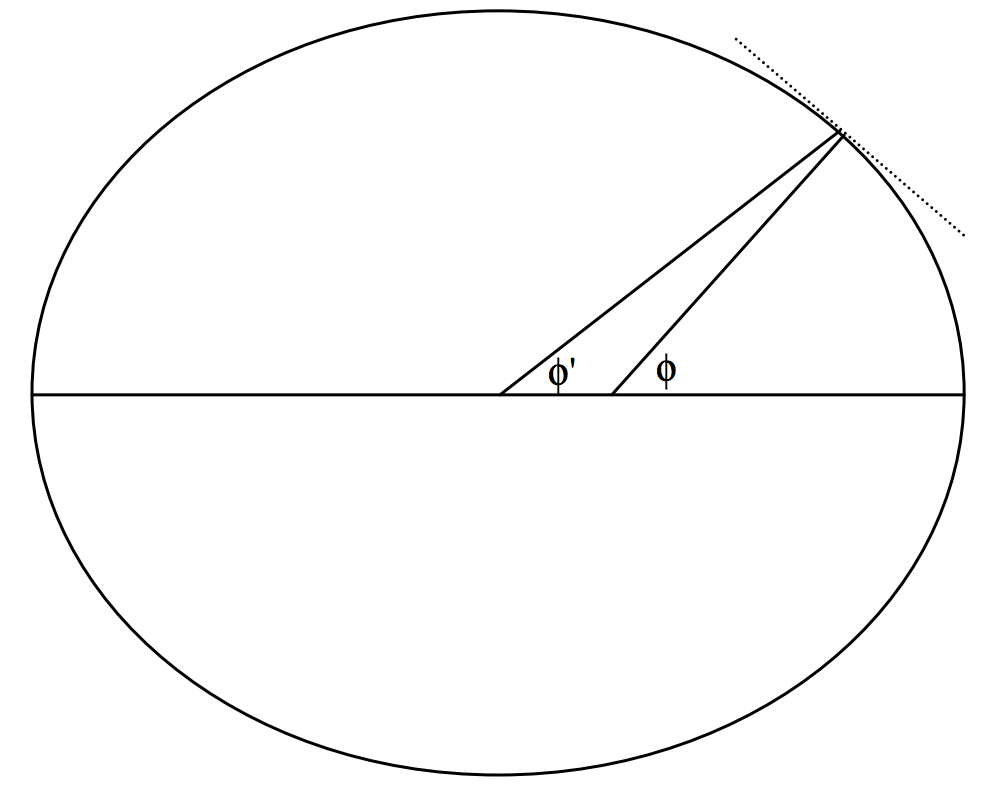
The relationship between \(\phi\) and \(\phi^\prime\) is
\[\phi - \phi^\prime = 692^\prime . 74 \sin 2 \phi - 1^\prime .16 \sin 4 \phi .\]


