4.2: Planes and Straight Lines

The geometry of the plane and the straight line is, of course, rather simple, so that we can dispose of them in this brief introductory section in a mere 57 Equations.

The Equation

$$Ax + By + Cz + D = 0 \label{4.2.1} \tag{4.2.1}$$

represents a plane. If $D$ ≠ 0 it is often convenient, and saves algebra and computation with no loss of information, to divide the Equation through by $D$ and re-write it in the form

$$ax + by + cz = 1. \label{4.2.2} \tag{4.2.2}$$

The coefficients need not by any means all be positive. If $D = 0$, the plane passes through the origin of coordinates, and it may be convenient to divide the Equation $\ref{4.2.1}$ by $C$ and hence to rewrite it in the form

$$ax + by + z = 0. \label{4.2.3} \tag{4.2.3}$$

The plane represented by Equation $\ref{4.2.2}$ intersects the $yz$-, $zx$- and $xy$-planes in the straight lines

$$by + cz = 1 \label{4.2.4} \tag{4.2.4}$$

$$cz + ax = 1 \label{4.2.5} \tag{4.2.5}$$

$$ax + by = 1 \label{4.2.6} \tag{4.2.6}$$

and it intersects the $x$-, $y$- and $z$-axes at

$$x = x_0 = 1/a \label{4.2.7} \tag{4.2.7}$$

$$y = y_0 = 1/b \label{4.2.8} \tag{4.2.8}$$

$$z = z_0 = 1/c \label{4.2.9} \tag{4.2.9}$$

The geometry can be seen in figure $\text{IV.1}$

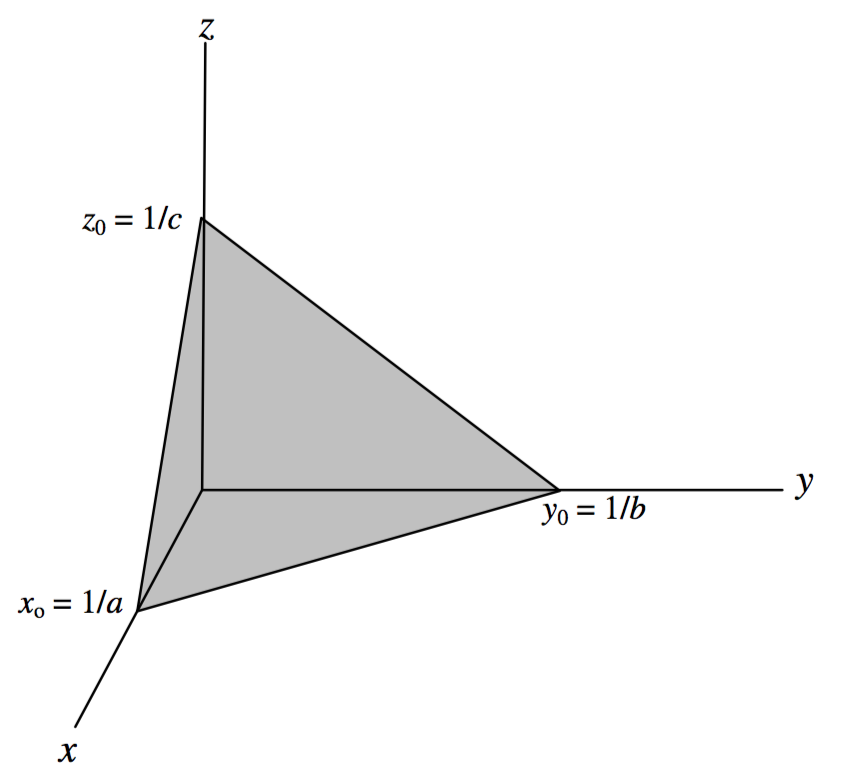
$\text{FIGURE IV.1}$

Another way of writing the Equation to the plane would be

$$\frac{x}{x_0} + \frac{y}{y_0} + \frac{z}{z_0} = 1. \label{4.2.10} \tag{4.2.10}$$

In this form, $x_0$, $y_0$ and $z_0$ are the intercepts on the $x$-, $y$- and $z$-axes.

Distance of a point from the plane

We now consider this problem. Let $\text{P}_1 \ (x_1 ,y_1 ,z_1 )$ be some point in space. What is the perpendicular distance from $\text{P}_1$ to the plane $ax + by + cz = \frac{x}{x_0} + \frac{y}{y_0} + \frac{z}{z_0} = 1$?

[The algebra in the following paragraphs may seem a little heavy. If all you are interested in is the distance of the plane from the origin, simply substitute $x_1 = y_1 = z_1 = 0$, and the algebra will be considerably eased.]

Let $\text{P}(x, y, z)$ be a point on the plane. The distance $s$ between $\text{P}_1$ and $\text{P}$ is given by

$$s^2 = (x-x_1)^2 + (y-y_1)^2 + (z-z_1)^2 \label{4.2.11} \tag{4.2.11}$$

But since $(x, y, z)$ is on the plane, we can write $s^2$ in terms of $x$ and $y$ alone, by substituting for $z$ from Equation $\ref{4.2.2}$:

$$s^2 = (x-x_1)^2 + (y-y_1)^2 + \left( \frac{1-ax-by}{c} - z_1 \right)^2 \label{4.2.12} \tag{4.2.12}$$

This distance (from $\text{P}$ to $\text{P}_1$) is least for a point on the plane such that $\frac{\partial s^2}{\partial x}$ and $\frac{∂s^2}{∂y}$ are both zero. These two conditions result in

$$(a^2 + c^2) x = a + c^2 x_1 - acz_1 - aby \label{4.2.13} \tag{4.2.13}$$

$$(b^2 + c^2) y = b + c^2 y_1 - bcz_1 - abx \label{4.2.14} \tag{4.2.14}$$

These, combined with Equation $\ref{4.2.2}$, result in

$$x = \frac{(b^2 + c^2)x_1 + a(1-by_1-cz_1)}{a^2 + b^2 + c^2} \label{4.2.15} \tag{4.2.15}$$

$$y = \frac{(c^2 + a^2) y_1 + b(1-cz_1 - ax_1)}{a^2 + b^2 + c^2} \label{4.2.16} \tag{4.2.16}$$

$$z = \frac{(a^2 +b^2) z_1 + c(1-ax_1 - by_1)}{a^2 + b^2 + c^2} \label{4.2.17} \tag{4.2.17}$$

These are the coordinates of the point $\text{P}$ in the plane that is nearest to $\text{P}_1$. The perpendicular distance between $\text{P}$ and $\text{P}_1$ is

$$p = \frac{1-ax_1-by_1-cz_1}{\sqrt{a^2 + b^2 + c^2}} \label{4.2.18} \tag{4.2.18}$$

This is positive if $\text{P}_1$ is on the same side of the plane as the origin, and negative if it is on the opposite side. If the perpendicular distances of two points from the plane, as calculated from Equation 4.4.18, are of opposite signs, they are on opposite sides of the plane. If $p = 0$, or indeed if the numerator of Equation 4.4.18 is zero, the point $\text{P}_1 (x_1 , y_1 , z_1 )$ is, of course, in the plane.

It is worthwhile to repeat these results for the case where the point $\text{P}_1$ coincides with the origin $\text{O}$. In that case we find that the coordinates of the point $\text{P}$ on the plane that is nearest to the origin are

$$x = \frac{a}{a^2 + b^2 + c^2}, \quad y = \frac{b}{a^2 + b^2 + c^2}, \quad z = \frac{c}{a^2 + b^2 + c^2}, \label{4.2.19a,b,c} \tag{4.2.19a,b,c}$$

and the perpendicular distance from the origin to the plane (i.e. from $\text{O}$ to $\text{P}$) is

$$p = \frac{1}{\sqrt{a^2 + b^2 + c^2}} \label{4.2.20} \tag{4.2.20}$$

Further, $\text{OP}$ is normal to the plane, and the direction cosines (see Chapter 3, especially section 3.3) of $\text{OP}$, i.e. of the normal to the plane, are

$$\frac{a}{\sqrt{a^2 + b^2 + c^2}}, \quad \frac{b}{\sqrt{a^2 + b^2 + c^2}}, \quad \frac{c}{\sqrt{a^2 + b^2 + c^2}} \tag{4.2.21} \label{4.2.21}$$

The coefficients $a$, $b$, $c$ are direction ratios of the normal to the plane; that is to say, they are numbers that are proportional to the direction cosines.

Example: Consider the plane

$$0.5x + 0.25y + 0.20z = 1 \label{4.2.22} \tag{4.2.22}$$

The plane intersects the $x$-, $y$- and $z$-axes at $(2,0,0), \ 0,4,0)$ and $(0,0,5)$. The point on the plane that is closest to the origin is $(1.4184, 0.7092, 0.5674)$. The perpendicular distance of the origin from the plane is $1.6843$. The direction cosines of the normal to the plane are $(0.8422, 0.4211, 0.3369)$.

An Equation for the plane containing three specified points can be found as follows. Let $(x_1 , y_1 )$, $(x_2 , y_2 )$, $(x_3 , y_3 )$ be the three specified points, and let $(x , y)$ be any point in the plane that contains these three points. Each of these points must satisfy an Equation of the form 4.2.1. That is,

$$xA + yB + zC + D = 0 \label{4.2.24} \tag{4.2.24}$$

$$x_1 A + y_1 B + z_1 C + D = 0 \label{4.2.25} \tag{4.2.25}$$

$$x_2 A + y_2 B + z_2 C + D = 0 \label{4.2.26} \tag{4.2.26}$$

$$x_3 A + y_3 B + z_3 C + D = 0 \label{4.2.27} \tag{4.2.27}$$

In these Equations, we are treating $A$, $B$, $C$, $D$ as unknowns, and the $x$, $y$, $z$, $x_1$, $y_1$... as coefficients. We have four linear Equations in four unknowns, and no constant term. From the theory of Equations, these are consistent only if each is a linear combination of the other three. This is satisfied only if the determinant of the coefficients is zero:

$$\begin{array}{| c c c c | c} x & y & z & 1 \\ x_1 & y_1 & z_1 & 1 & = 0 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ \label{4.2.28} \tag{4.2.28} \end{array}$$

and this is the Equation to the required plane containing the three points. The reader will notice the similarity of this Equation to Equation 2.2.4 for a line passing between two points in two-dimensional geometry. The reader might like to repeat the argument, but requiring instead the four points to satisfy an Equation of the form 4.2.2. There will then be four linear Equations in three unknowns. Otherwise the argument is the same.

We now move on to the question of finding the area of a triangle whose vertices are given. It is straightforward to do this with a numerical example, and the reader is now encouraged to write a computer program, in whatever language is most familiar, to carry out the following tasks. Read as data the $x$-$y$-$z$ coordinates of three points $\text{A, B, C}$. Calculate the lengths of the sides $a$, $b$, $c$, a being opposite to $\text{A}$, etc. Calculate the three angles at the vertices of the triangle, in degrees and minutes, and check for correctness by verifying that their sum is $180^\circ$. If an angle is obtuse, make sure that the computer displays its value as a positive angle between $90^\circ$ and $180^\circ$. Finally, calculate the area of the triangle.

The data for several triangles could be written into a data file, which your program reads, and then writes the answers into an output file. Alternatively, you can type the coordinates of the vertices of one triangle and ask the computer to read the data from the monitor screen, and then to write the answers on the screen followed by a message such as "Do you want to try another triangle (1) or quit (2)?". Your program should also be arranged so that it writes an appropriate message if the three points happen to be collinear.

It should be easy to calculate the sides. The angles can then be calculated from Equation 3.2.2 and the area from each of the four Equations 3.2.3 and 3.2.4. They should all yield the correct answer, of course, but the redundant calculations serve as an important check on the correctness of your programming, as also does your check that the three angles add to $180^\circ$. Where there are two of more ways of performing a calculation, a careful calculator will do all of them as a check against mistakes, whether the calculation is done by hand or by computer.

Example. If the coordinates of the vertices are

$$\text{A}(7, 4, 3), \quad \text{B}(11, 6, 2), \quad \text{C}(9,2,4)$$

the sides are $$a=4.899, \quad b=3.000, \quad c=4.583,$$

and the angles are $$A = 65^\circ 55^\prime , \quad B = 36^\circ 42^\prime , C = 77^\circ 23^\prime ,$$

which add up to $180^\circ$. The area is $6.708$.

Example. If the coordinates of the vertices are

$$\text{A}(6,4,9), \quad \text{B}(2,6,17), \quad \text{C}(8,3,5)$$

the area of the triangle is zero and the points are collinear.

The foregoing showed that it was not difficult to calculate numerically the area of the triangle from the coordinates of its vertices. Is it easy to find a simple explicit algebraic formula for the area in terms of $(x_1 , y_1 , z_1 )$, $(x_2 , y_2 , z_2 )$ and $(x_3 , y_3 , z_3 )$? On referring to figure $\text{IV.2}$, we can proceed as follows.

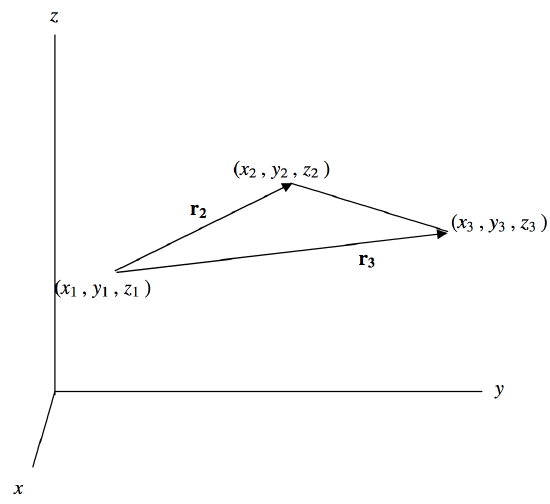
$\text{FIGURE IV.2}$

The vectors $\textbf{r}_2$ and $\textbf{r}_3$ can be written

$$\textbf{r}_2 = (x_2 - x_1) \textbf{i} + (y_2 - y_1) \textbf{j} + (z_2 - z_1) \textbf{k} \label{4.2.29} \tag{4.2.29}$$

$$\textbf{r}_3 = (x_3 - x_1) \textbf{i} + (y_3 - y_1) \textbf{j} + (z_3 - z_1) \textbf{k} \label{4.2.30} \tag{4.2.30}$$

where $\textbf{i, j, k}$ are unit vectors parallel to the $x$-, $y$- and $z$- axes.

The cross product of $\textbf{r}_2$ and $\textbf{r}_3$ gives the (vector) area of the parallelogram of which they form two sides. The area $\textbf{A}$ of the triangle is half of this, so that

$$2 \textbf{A} = \textbf{r}_2 \times \textbf{r}_3$$
$$= [(y_2 - y_1) (z_3 - z_1) - (y_3 - y_1) (z_2 - z_1)] \textbf{i}$$
$$+[(z_2 - z_1) (x_3 - x_1) - (z_3 - z_1) (x_2 - x_1)] \textbf{j}$$
$$+[(x_2 - x_1) (y_3 - y_1) - (x_3 - x_1) (y_2 - y_1)] \textbf{k} \label{4.2.31} \tag{4.2.31}$$

The magnitude of this vector can be found in the usual way, to obtain

$$4A^2 = [(y_1 (z_2 - z_3) + y_2 (z_3 - z_1) + y_3 (z_1 - z_2)]^2$$
$$+[(z_1(x_2 - x_3) + z_2( x_3 - x_1) + z_3(x_1 - x_2)]^2$$
$$+[(x_1 (y_2 - y_3) + x_2 (y_3 - y_1) + x_3 ( y_1 - y_2)]^2. \label{4.2.32} \tag{4.2.32}$$

The reader can verify that, if $z_1 = z_2 = z_3$, this reduces to Equation 2.2.12 for the area of a triangle the $xy$-plane. Equation 4.1.32 can also be written

$$4A^2 = \begin{vmatrix} y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \\ 1 & 1 & 1 \end{vmatrix}^2 + \begin{vmatrix} z_1 & z_2 & z_3 \\ x_1 & x_2 & x_3 \\ 1 & 1 & 1 \end{vmatrix}^2 + \begin{vmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{vmatrix}^2 \label{4.2.33} \tag{4.2.33}$$

This gives the area explicitly in terms of the coordinates of the vertices. If it is zero, the points are collinear.

The volume of a tetrahedron is $\frac{1}{6} \times \text{base} \times \text{height}$. By combining Equation $\ref{4.2.33}$ for the area of a triangle with Equation $\ref{4.2.14}$ for the perpendicular distance of a point from a plane, we can determine that the volume of the tetrahedron whose vertices are

$$(x_0, y_0, z_0), \ (x_1, y_1, z_1), \ (x_2, y_2, z_2), \ (x_3, y_3, z_3)$$

is $$\frac{1}{6} \begin{vmatrix} x_0 & y_0 & z_ 0 & 1 \\ x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \end{vmatrix} \label{4.2.34} \tag{4.2.34}$$

If this determinant is zero, the four points are coplanar.

In three-dimensional coordinate geometry, a straight line is described by two Equations, being the intersection of two planes:

$$a_1 x + b_1 y + c_1 z = 1 \label{4.2.35} \tag{4.2.35}$$

$$a_2 x + b_2 y + c_2 z = 1 \label{4.2.36} \tag{4.2.36}$$

If $a_1/a_2 = b_1/b_2 = c_1/c_2$,the normals to the two planes have the same direction ratios, so the planes are parallel and do not intersect. Otherwise the normals to the two planes have different direction ratios $(a_1 , b_1 , c_1 ), \ (a_2 , b_2 , c_2 )$, and, since the line of intersection of the planes is at right angles to both normals, the direction ratios of the line are found from the cross product of vectors normal to the planes. The direction ratios of the line of intersection are therefore

$$(b_1 c_2 - b_2 c_1 , \ c_1 a_2 - c_2 a_1 , \ a_1 b_2 - a_2 b_1 ) \label{4.2.37} \tag{4.2.37}$$

The line crosses the $yz$-, $zx$- and $xy$- planes at

$$y = \frac{c_2 - c_1}{b_1 c_2 - b_2 c_1} \quad z = \frac{b_1 - b_2}{b_1 c_2 - b_2 c_1} \label{4.2.38} \tag{4.2.38}$$

$$z = \frac{a_2 - a_1}{c_1 a_2 - c_2 a_1} \quad x = \frac{c_1 - c_2}{c_1 a_2 - c_2 a_1} \label{4.2.39} \tag{4.2.39}$$

$$x = \frac{b_2 - b_1}{a_1 b_2 - a_2 b_1} \quad y = \frac{a_1 - a_2}{a_1 b_2 - a_2 b_1} \label{4.2.40} \tag{4.2.40}$$

An example of computing a straight line from the intersection of two planes occurs in meteor astronomy. We can assume a flat Earth, which is tantamount to supposing that the height of a meteor is negligible compared with the radius of Earth, and the height of an observer above sea level is negligible compared with the height of the meteor. Since the heights of meteors are typically a few tens of km, both of these approximations are reasonable, at least for noninstrumental eyewitness accounts.

We suppose that, relative to an arbitrary origin $\text{O}$ on the surface of Earth, a witness $\text{A}$ is $15 \ \text{km east}$ and $5 \ \text{km north}$ of the origin. He sees a fireball start at an angle $θ = 25^\circ .5$ from his zenith and at an azimuth $\phi = 54^\circ .5$ counterclockwise from his east, and it finishes at $θ = 36^\circ .7$, $\phi = 16^\circ .7$. (See figure $\text{IV.3}$.)

Show that the plane containing the witness and the meteor is

$$0.0363x + 0.0911y - 0.0454z = 1 \label{4.2.41} \tag{4.2.41}$$

A second witness, $30 \text{ km east}$ and $15 \text{ km north}$ of $\text{O}$, estimates the zenith distance and azimuth of two points on the meteor track to be $θ = 29^\circ .6$, $\phi = 202^\circ .9$ and $θ = 33^\circ .6$, $\phi = 242^\circ .9$

Show that the plane containing this second witness and the meteor is

$$0.0257x + 0.0153y + 0.0168z =1 \label{4.2.42} \tag{4.2.42}$$

These two Equations describe the path of the fireball through the air. Show that, if the meteoroid carries on moving in a straight line, it will strike the ground as a meteorite $42.4 \text{ km east}$ and $6.0 \text{ km south}$ of the origin $\text{O}$.

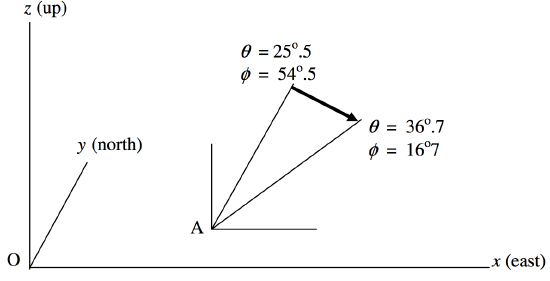
$\text{FIGURE IV.3}$

As we have just discussed, two nonparallel planes intersect in a straight line. Usually, three nonparallel planes intersect at a single unique point; for, if $\text{L}$ is a line formed from the intersection of planes $\text{P}_1$ and $\text{P}_2$, $L$ will usually intersect the plane $\text{P}_3$ at a point.

Example: The planes

$$2x + 3y + 4z - 9 = 0 \label{4.2.43} \tag{4.2.43}$$

$$x + y -8z + 6 = 0 \label{4.2.44} \tag{4.2.44}$$

$$5x + 6y - 12z + 1 = 0 \label{4.2.45} \tag{4.2.45}$$

intersect at $(1, 1, 1)$.

It will be recalled from the theory of linear Equations that three Equations

$$A_1 x + B_1 y + C_1 z + D_1 = 0 \label{4.2.46} \tag{4.2.46}$$

$$A_2 x + B_2 y + C_2z + D_2 = 0 \label{4.2.47} \tag{4.2.47}$$

$$A_3x + B_3 y + C_3 z + D_3 = 0 \label{4.2.48} \tag{4.2.48}$$

have a unique solution only if

$$\Delta = \begin{vmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_2 & C_3 \\ \end{vmatrix} \neq 0 \label{4.2.49} \tag{4.2.49}$$

and, in the geometrical interpretation, this is the condition that three planes meet in a single point. Consider, however, the three planes

$$2x + 3y + 4z - 9 = 0 \label{4.2.50} \tag{4.2.50}$$

$$x + y - 8z + 6 = 0 \label{4.2.51} \tag{4.2.51}$$

$$5x + 6y -20z + 12 = 0 \label{4.2.52} \tag{4.2.52}$$

The direction ratios of the three lines found by combining the planes in pairs (see Equation $\ref{4.2.37}$) are

$$(-28, 20, -1) \quad (-84, 60, -3) \quad (28, -20, 1)$$

It will be observed that each is a multiple of either of the others, and the direction cosines of each of the three lines are identical apart from sign: $( \mp 0.813, \pm 0.581, \mp 0.029)$.

The three lines are, in fact, parallel, and the three planes enclose a prism. A condition for this is that

$$\Delta = 0. \label{4.2.53} \tag{4.2.53}$$

But consider now the planes

$$2x + 3y + 4z - 9 = 0 \label{4.2.54} \tag{4.2.54}$$

$$x + y - 8z + 6 = 0 \label{4.2.55} \tag{4.2.55}$$

$$5x + 6y - 20z + 9 = 0 \label{4.2.56} \tag{4.2.56}$$

Not only does $\Delta = 0$, but also

$$\Delta^\prime = \begin{vmatrix} A_1 & B_1 & D_1 \\ A_2 & B_2 & D_2 \\ A_3 & B_3 & D_3 \\ \end{vmatrix} = 0 \label{4.2.57} \tag{4.2.57}$$

The three lines obtained by combining Equations 4.2.54,55,56 in pairs are in fact identical, and the three planes meet in a single line. Each of Equations 4.2.54,55,56 is a linear combination of the other two.

In summary, three nonparallel planes meet in a single line if $∆ \neq 0$. They meet in a single point if $∆ = ∆^\prime = 0$. They enclose a prism if $∆ = 0, ∆^\prime \neq 0$.