4.3: The Ellipsoid

Consider the Equation

$$\frac{x^2}{a^2} + \frac{z^2}{c^2} = 1, \label{4.3.1} \tag{4.3.1}$$

with $a > c$, in the $xz$-plane. The length of the semi major axis is $a$ and the length of the semi minor axis is $c$. If this figure is rotated through $360^\circ$ about its minor ($z$-) axis, the three- dimensional figure so obtained is called an oblate spheroid. The figure of the Earth is not exactly spherical; it approximates to a very slightly oblate spheroid, the ellipticity $(c − a)/a$ being only $0.00335$. (The actual figure of the Earth, mean sea level, is often referred to as the geoid.)

The Equation to the oblate spheroid referred to above is

$$\frac{x^2}{a^2} + \frac{y^2}{a^2} + \frac{z^2}{c^2} = 1. \label{4.3.2} \tag{4.3.2}$$

If the ellipse $\ref{4.3.1}$ is rotated through $360^\circ$ about its major ($x$-) axis, the figure so obtained is called a prolate spheroid. A rugby football (or, to a lesser extent, a North American football, which is a bit too pointed) is a good approximation to a prolate spheroid.

The Equation to the prolate spheroid just described is

$$\frac{x^2}{a^2} + \frac{y^2}{c^2} + \frac{z^2}{c^2} = 1. \label{4.3.3} \tag{4.3.3}$$

Either type of spheroid can be referred to as an "ellipsoid of revolution".

The figure described by the Equation

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 \label{4.3.4} \tag{4.3.4}$$

is a tri-axial ellipsoid. Unless stated otherwise, I shall adopt the convention $a > b > c$, and choose the coordinate axes such that the major, intermediate and minor axes are along the $x$-, $y$- and $z$-axes respectively. A tri-axial ellipsoid is not an ellipsoid of revolution; it cannot be obtained by rotating an ellipse about an axis.

The special case $a = b = c$:

$$x^2 + y^2 + z^2 = a^2 \label{4.3.5} \tag{4.3.5}$$

is, of course, a sphere.

Figure $\text{IV.4}$ shows the cross-section of a tri-axial ellipse in the $yz$- plane (a), the $xz$-plane (b) and (twice - (c), (d)) the $xy$-plane. If you imagine your eye wandering in the $xz$-plane from the $x$-axis (a) to the $z$-axis (c), you will be convinced that there is a direction in the $xz$-plane from which the

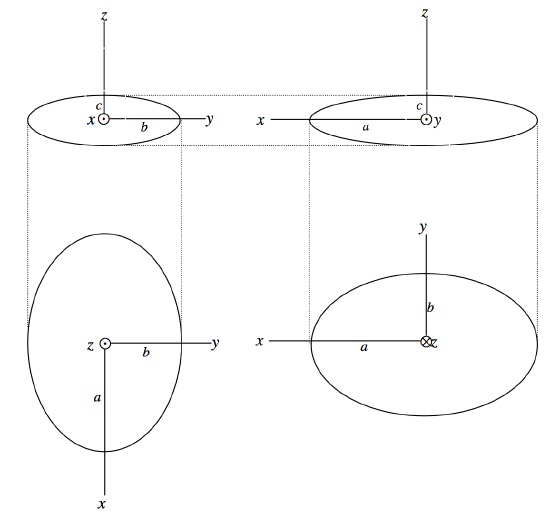
$\text{FIGURE IV.4}$

cross-section of the ellipse is a circle. There are actually two such directions, symmetrically situated on either side of the $z$-axis, but there are no such directions in either the $xy$- or the $yz$-planes from which the cross-section of the ellipsoid appears as a circle. Expressed otherwise, there are two planes that intersect the ellipsoid in a circle. This fact is of some importance in the description of the propagation of light in a bi-axial crystal, in which one of the wavefronts is a tri-axial ellipsoid.

Let us refer the ellipsoid $\ref{4.3.4}$ to a set of axes $\text{O}x^\prime y^\prime z^\prime$ such that the angles $z^\prime \text{O} z$ and $x^\prime \text{O} x$ are each $θ$, and the $y^\prime$- and $y$-axes are identical. The Equation of the ellipsoid referred to the new axes is (by making use of the usual formulas for the rotation of axes)

$$\frac{(z^\prime \sin θ + x^\prime \cos θ)^2}{a^2} + \frac{y^{\prime 2}}{b^2} + \frac{(z^\prime \cos θ - x^\prime \sin θ)^2}{c^2} = 1. \label{4.3.6} \tag{4.3.6}$$

The cross-section of the ellipsoid in the $x^\prime y^\prime$-plane (i.e. normal to the $z^\prime$-axis) is found by putting $z^\prime = 0$:

$$\frac{(x^\prime \cos θ)^2}{a^2} + \frac{y^{\prime 2}}{b^2} + \frac{(x^\prime \sin θ)^2}{c^2} = 1. \label{4.3.7} \tag{4.3.7}$$

This is a circle if the coefficients of $x^\prime$ and $y^\prime$ are equal. Thus it is a circle if

$$\cos^2 θ = \frac{a^2(b^2 - c^2)}{b^2(a^2 - c^2)}. \label{4.3.8} \tag{4.3.8}$$

Thus, a plane whose normal is in the $xz$-plane (i.e. between the major and minor axis) and inclined at an angle $θ$ to the minor ($z$-) axis, cuts the tri-axial ellipsoid in a circle. As viewed from either of these directions, the cross-section of the ellipsoid is a circle of radius $b$.

As an asteroid tumbles over and over, its brightness varies, for several reasons, such as its changing phase angle, the directional reflective properties of its regolith, and, of course, the cross-sectional area presented to the observer. The number of factors that affect the light-curve of a rotating asteroid is, in fact, so large that it is doubtful if it is possible, from the light-curve alone, to deduce with much credibility or accuracy the true shape of the asteroid. However, it is obviously of some interest for a start in any such investigation to be able to calculate the cross-sectional area of the ellipsoid $\ref{4.3.3}$ as seen from some direction $( θ , \phi )$.

Let us erect a set of coordinate axes $\text{O}x^\prime y^\prime z^\prime$ such that $\text{O} z^\prime$ is in the direction $( θ , \phi )$, first by a rotation through $\phi$ about $\text{O}z$ to form intermediate axes $\text{O}x_1 y_1 z_1$, followed by a rotation through $θ$ about $\text{O} y_1$. The $(x^\prime , y^\prime , z^\prime )$ coordinates are related to the $(x, y, z)$ coordinates by

$$\pmatrix{x \\ y \\ z} = \pmatrix{\cos \phi & -\sin \phi & 0 \\ \sin \phi & \cos \phi & 0 \\ 0 & 0 & 1} \pmatrix{\cos θ & 0 & \sin θ \\ 0 & 1 & 0 \\ -\sin θ & 0 & \cos θ} \pmatrix{x^\prime \\ y^\prime \\ z^\prime} \label{4.3.9} \tag{4.3.9}$$

If we substitute for $x, \ y, \ z$ in Equation $\ref{4.3.4}$ from Equation $\ref{4.3.9}$, we obtain the Equation to the ellipsoid referred to the $\text{O} x^\prime y^\prime z^\prime$ coordinate systems. And if we put $z^\prime = 0$, we see the elliptical crosssection of the ellipsoid in the plane normal to $\text{O}z^\prime$. This will be of the form

$$Ax^{\prime 2} + 2H x^\prime y^\prime + B y^{\prime 2} = 1, \label{4.3.10} \tag{4.3.10}$$

where $$A = \cos^2 θ \left( \frac{\cos^2 \phi}{a^2} + \frac{\sin^2 \phi}{b^2} \right) + \frac{\sin^2 θ}{c^2} \label{4.3.11} \tag{4.3.11}$$

$$2H = 2 \cos θ \sin \phi \cos \phi \left( \frac{1}{b^2} - \frac{1}{a^2} \right) , \label{4.3.12} \tag{4.3.12}$$

$$B = \frac{\sin^2 \phi}{a^2} + \frac{\cos^2 \phi}{b^2}. \label{4.3.13} \tag{4.3.13}$$

This is an ellipse whose axes are inclined at an angle $ψ$ from $\text{O}x^\prime$ given by

$$\tan 2 ψ = \frac{2H}{A-B}. \label{4.3.14} \tag{4.3.14}$$

By replacing $x^\prime$ and $y^\prime$ by $x^{\prime \prime}$ and $y^{\prime \prime}$, where

$$\pmatrix{x^\prime \\ y^\prime} = \pmatrix{\cosψ & - \sin ψ \\ \sin ψ & \cos ψ} \pmatrix{x^{\prime \prime} \\ y^{\prime \prime}} \label{4.3.15} \tag{4.3.15}$$

we shall be able to describe the ellipse in a coordinate system $\text{O}x^{\prime \prime}y^{\prime \prime}$ whose axes are along the axes of the ellipse, and the Equation will be of the form

$$\frac{x^{\prime \prime 2}}{a^{\prime \prime 2}} + \frac{y^{\prime \prime 2}}{b^{\prime \prime 2}} = 1 \label{4.3.16} \tag{4.3.16}$$

and the area of the cross-section is $\pi a^{\prime \prime} b^{\prime \prime}$.

For example, suppose the semi axes of the ellipsoid are $a = 3, \ b = 2, \ y = 1$, and we look at it from the direction $θ = 60^\circ$, $\phi= 45^\circ$. Following Equations 4.4.9,10,11,12, we obtain for the Equation of the elliptical cross-section referred to the system $\text{O}x^\prime y^\prime z^\prime$

$$0.79513 \dot{8} x^{\prime 2} + 0.069 \dot{4} x^\prime y^\prime + 0.180 \dot{5} y^{\prime 2} = 1 . \label{4.3.17} \tag{4.3.17}$$

From Equation 4.4.13 we find $ψ = 3^\circ\ .22338$. Equation 4.4.14 then transforms Equation 4.4.16 to

$$0.797094 x^{\prime \prime 2} + 0.178600 y^{\prime \prime 2} = 1 \label{4.3.18} \tag{4.3.18}$$

or $$\frac{x^{\prime \prime 2}}{(1.1201)^2} + \frac{y^{\prime \prime 2}}{(2.3662)^2} = 1. \label{4.3.19} \tag{4.3.19}$$

The area is $$\pi \times 1.1201 \times 2.3662 = 8.362.$$

It is suggested here that the reader could write a computer program in the language of his or her choice for calculating the cross-sectional area of an ellipsoid as seen from any direction. As an example, I reproduce below a Fortran program for an ellipse with $(a, b, c) = (3, 2, 1)$. It is by no means the fastest and most efficient Fortran program that could be written, but is sufficiently straightforward that anyone familiar with Fortran and probably many who are not should be able to follow the steps.

A=3.
B=2.
C=1.
A2=A*A
B2=B*B
C2=C*C
READ(5,*)TH,PH
TH=TH/57.29578
PH=PH/57.29578
STH=SIN(TH)
CTH=COS(TH)
SPH=SIN(PH)
CPH=COS(PH)
STH2=STH*STH
CTH2=CTH*CTH
SPH2=SPH*SPH
CPH2=CPH*CPH
AA=CTH2*(CPH2/A2+SPH2/B2)+STH2/C2
TWOHH=2.*CTH*SPH*CPH*(1./B2−1./A2)
BB=SPH2/A2+CPH2/B2
PS=.5*ATAN2(TWOHH,AA−BB)
SPS=SIN(PS)
CPS=COS(PS)
AAA=CPS*(AA*CPS+TWOHH*SPS)+BB*SPS*SPS
BBB=SPS*(AA*SPS−TWOHH*CPS)+BB*CPS*CPS
SEMAX1=1./SQRT(AAA)
SEMAX2=1./SQRT(BBB)
AREA=3.1415927*SEMAX1*SEMAX2
WRITE(6,1)AREA
1 FORMAT(' Area = ',F7.3)
STOP
END