8.3: Sidereal and Synodic Periods
( \newcommand{\kernel}{\mathrm{null}\,}\)
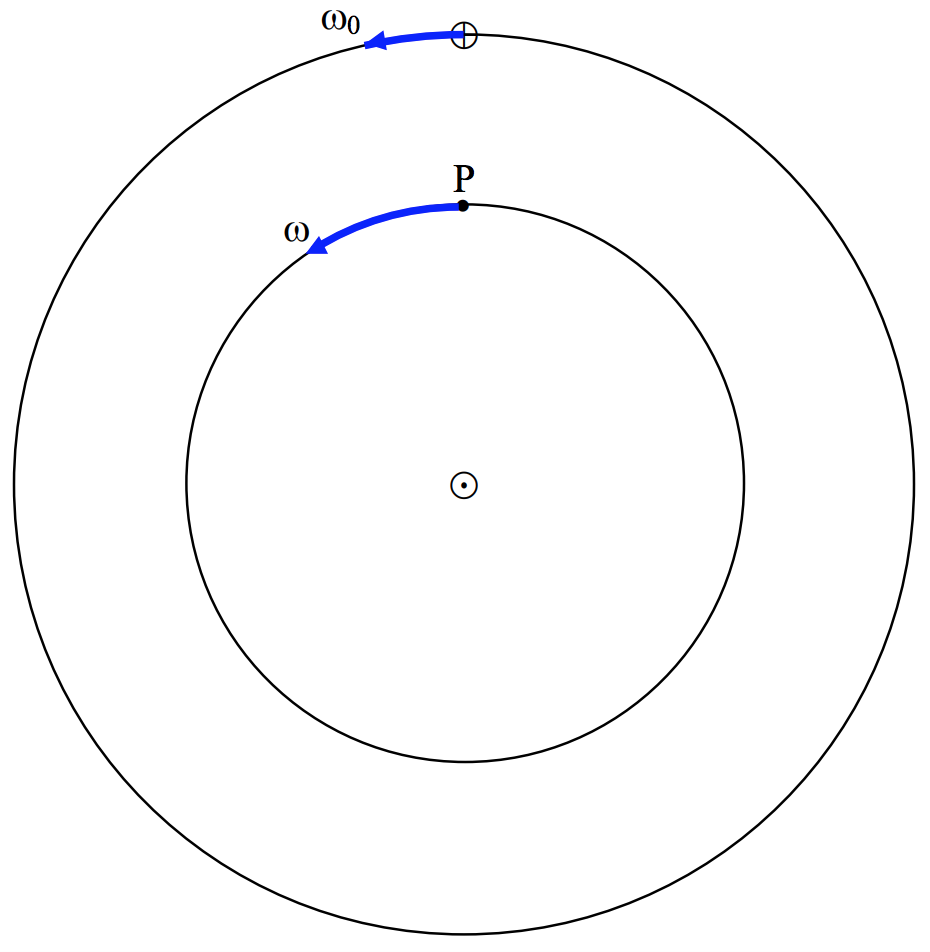
FIGURE VIII.3
Figure VIII.3 shows the orbits of Earth (⊕) and an inferior planet (P). Earth is moving around the Sun at angular speed ω0 and period P0=2π/ω0=1 sidereal year. The planet is moving around the Sun at a faster angular speed ω and shorter period Psid=2π/ω, which is called the sidereal period of the planet (i.e. the period relative to the fixed stars). The angular speed of the planet with respect to Earth is ωPE=ω−ω0. The interval between two consecutive inferior conjunctions of the planet is called its synodic period, Psyn, and is equal to 2π/ωPE. Thus, since the relation between angular speed and period is ω=2π/P, we see that
1Psyn=1Psid−1P0.(inferior planet)
The reader can draw the situation for a superior planet, and will see that in that case ωPE=ω0−ω. The synodic period of the planet is the interval between two consecutive oppositions, and we arrive at
1Psyn=1P0−1Psid.(superior planet)
Of all the major planets, Mars has the longest synodic period, namely 780 days, so that it comes to opposition and is easy to observe at intervals of a little more than two years. Mercury has the shortest synodic period, namely 116 days. The synodic periods of all superior planets are greater than one sidereal year. The synodic periods of inferior planets may be less than (Mercury) or greater that (Venus) one sidereal year.
An inferior planet in a circular orbit has a synodic period of one sidereal year. What is the radius of its orbit?


