1.4: The Solution of f(x) = 0

The title of this section is intended to be eye-catching. Some Equations are easy to solve; others seem to be more difficult. In this section, we are going to try to solve any Equation at all of the form \(f(x) = 0\) (which covers just about everything!) and we shall in most cases succeed with ease.

Figure I.3 shows a graph of the Equation \(y = f(x)\). We have to find the value (or perhaps values) of \(x\) such that \(f(x) = 0\).

We guess that the answer might be \(x_g\), for example. We calculate \(f(x_g)\). It won't be zero, because our guess is wrong. The figure shows our guess \(x_g\), the correct value \(x\), and \(f(x_g)\). The tangent of the angle \(\theta\) is the derivative \(f^\prime (x)\), but we cannot calculate the derivative there because we do not yet know \(x\). However, we can calculate \(f^\prime (x_g)\), which is close. In any case \(\tan \theta\), or \(f^\prime (x_g)\), is approximately equal to \(f(x_g)/(x_g- x)\), so that

\[x \approx x_g - \frac{f(x_g)}{f^\prime (x_g)} \label{1.4.1}\]

will be much closer to the true value than our original guess was. We use the new value as our next guess, and keep on iterating until

\[\left| \frac{x_g - x}{x_g} \right| \nonumber\]

is less than whatever precision we desire. The method is usually extraordinarily fast, even for a wildly inaccurate first guess. The method is known as Newton-Raphson iteration. There are some cases where the method will not converge, and stress is often placed on these exceptional cases in mathematical courses, giving the impression that the Newton-Raphson process is of limited applicability. These exceptional cases are, however, often artificially concocted in order to illustrate the exceptions (we do indeed cite some below), and in practice Newton-Raphson is usually the method of choice.

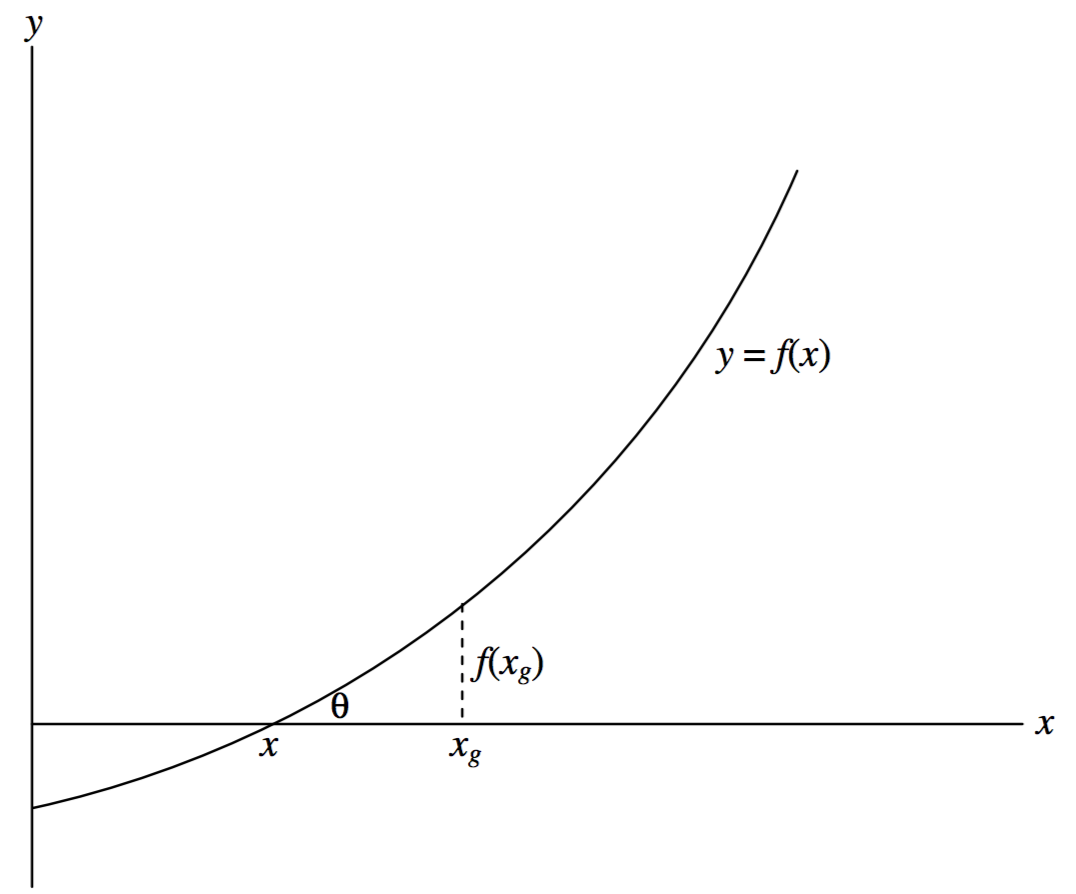
\(\text{FIGURE I.3}\)

I shall often drop the clumsy subscript \(g\), and shall write the Newton-Raphson scheme as

\[x = x - f(x) / f^\prime (x) , \label{1.4.2}\]

meaning "start with some value of \(x\), calculate the right hand side, and use the result as a new value of \(x\)". It may be objected that this is a misuse of the \(=\) symbol, and that the above is not really an "Equation", since \(x\) cannot equal \(x\) minus something. However, when the correct solution for \(x\) has been found, it will satisfy \(f(x) = 0\), and the above is indeed a perfectly good Equation and a valid use of the \(=\) symbol.

Example \(\PageIndex{1}\)

Solve the Equation \(1/x = \ln x\)

We have \(f = 1/x - \ln x = 0\)

And \(f^\prime = -(1 + x)/ x^2\),

from which \(x − f / f^\prime\) becomes, after some simplification,

\[\frac{x[2 + x(1-\ln x)]}{1+x}, \nonumber\]

so that the Newton-Raphson iteration is

\[x = \frac{x[2 + x(1- \ln x )]}{1+x} . \nonumber\]

There remains the question as to what should be the first guess. We know (or should know!) that \(\ln 1 = 0\) and \(\ln 2 = 0.6931\), so the answer must be somewhere between \(1\) and \(2\). If we try \(x = 1.5\), successive iterations are

\begin{array}{c}
1.735 \ 081 \ 403 \\
1.762 \ 915 \ 391 \\
1.763 \ 222 \ 798 \\
1.763 \ 222 \ 834 \\
1.763 \ 222 \ 835 \\
\nonumber
\end{array}

This converged quickly from a fairly good first guess of \(1.5\). Very often the Newton-Raphson iteration will converge, even rapidly, from a very stupid first guess, but in this particular example there are limits to stupidity, and the reader might like to prove that, in order to achieve convergence, the first guess must be in the range

\[0 < x < 4.319 \ 136 \ 566 \nonumber\]

Example \(\PageIndex{2}\)

Solve the unlikely Equation \(\sin x = \ln x\)

We have \(f = \sin x - \ln x\) and \(f^\prime = \cos x - 1/x\),

and after some simplification the Newton-Raphson iteration becomes

\[x = x \left[ 1 + \frac{\ln x - \sin x}{x \cos x -1} \right] . \nonumber\]

Graphs of \(\sin x\) and \(\ln x\) will provide a first guess, but in lieu of that and without having much idea of what the answer might be, we could try a fairly stupid \(x = 1\). Subsequent iterations produce

\begin{array}{c}
2.830 \ 487 \ 722 \\
2.267 \ 902 \ 211 \\
2.219 \ 744 \ 452 \\
2.219 \ 107 \ 263 \\
2.219 \ 107 \ 149 \\
2.219 \ 107 \ 149 \\
\nonumber
\end{array}

Example \(\PageIndex{3}\)

Solve the Equation \(x^2 = a\) (A new way of finding square roots!)

\[ f= x^2 - a, \quad f^\prime = 2x. \nonumber\]

After a little simplification, the Newton-Raphson process becomes

\[x = \frac{x^2 + a}{2x}. \nonumber\]

For example, what is the square root of 10? Guess 3. Subsequent iterations are

\begin{array}{c}
3.166 \ 666 \ 667 \\
3.162 \ 280 \ 702 \\
3.162 \ 277 \ 661 \\
3.162 \ 277 \ 661 \\
\nonumber
\end{array}

Example \(\PageIndex{4}\)

Solve the Equation \(ax^2 + bx + c = 0\) (A new way of solving quadratic Equations!)

\[f = ax^2 + bx + c = 0, \nonumber\]

\[f^\prime = 2ax + b . \nonumber\]

Newton-Raphson:

\[x = x- \frac{ax^2 + bx + c}{2ax + b}, \nonumber\]

which becomes, after simplification,

\[x = \frac{ax^2-c}{2ax+b}. \nonumber\]

This is just the iteration given in the previous section, on the solution of quadratic Equations, and it shows why the previous method converged so rapidly and also how I really arrived at the Equation (which was via the Newton-Raphson process, and not by arbitrarily adding \(ax^2\) to both sides!)