5.4.10: Bubble Inside a Uniform Solid Sphere
( \newcommand{\kernel}{\mathrm{null}\,}\)
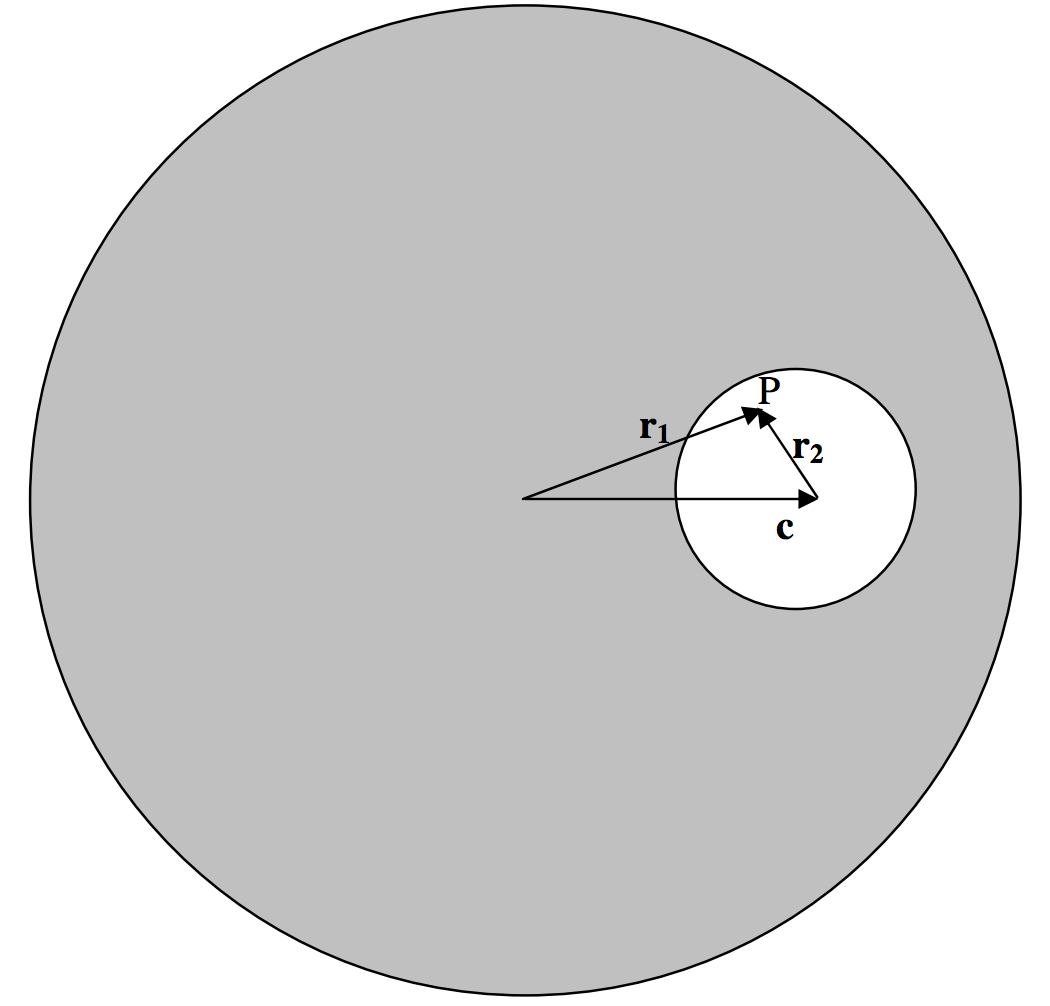
FIGURE V.11
P is a point inside the bubble. The field at P is equal to the field due to the entire sphere minus the field due to the missing mass of the bubble. That is, it is
g=−43πGρr1−(−43πGρr2)=−43πGρ(r1−r2)=−43πGρc.
That is, the field at P is uniform (i.e. is independent of the position of P) and is parallel to the line joining the centres of the two spheres.


