5.5: Gauss's Theorem
( \newcommand{\kernel}{\mathrm{null}\,}\)
Much of the above may have been good integration practice, but we shall now see that many of the results are immediately obvious from Gauss’s Theorem – itself a trivially obvious law. (Or shall we say that, like many things, it is trivially obvious in hindsight, though it needed Carl Friedrich Gauss to point it out!)
First let us define gravitational flux Φ as an extensive quantity, being the product of gravitational field and area:
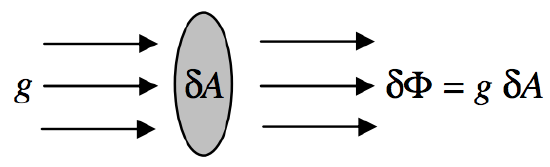
FIGURE V.12
If g and δA are not parallel, the flux is a scalar quantity, being the scalar or dot product of g and δA:
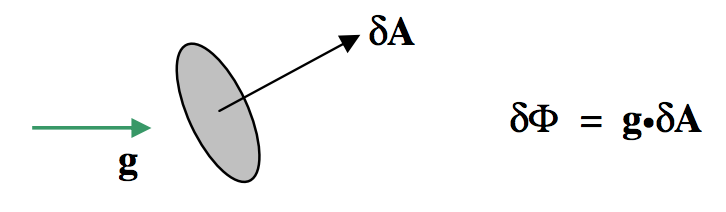
FIGURE V.13
If the gravitational field is threading through a large finite area, we have to calculate g•δA for each element of area of the surface, the magnitude and direction of g possibly varying from point to point over the surface, and then we have to integrate this all over the surface. In other words, we have to calculate a surface integral. We’ll give some examples as we proceed, but first let’s move toward Gauss’s theorem.
In figure V.14, I have drawn a mass M and several of the gravitational field lines converging on it. I have also drawn a sphere of radius r around the mass. At a distance r from the mass, the field is GM/r2. The surface area of the sphere is 4πr2. Therefore the total inward flux, the product of these two terms, is 4πGM, and is independent of the size of the sphere. (It is independent of the size of the sphere because the field falls off inversely as the square of the distance. Thus Gauss’s theorem is a theorem that applies to inverse square fields.) Nothing changes if the mass is not at the centre of the sphere. Nor does it change if (figure V.15) the surface is not a sphere. If there were several masses inside the surface, each would contribute 4πG times its mass to the total normal inwards flux. Thus the total normal inward flux through any closed surface is equal to 4πG times the total mass enclosed by the surface. Or, expressed another way:
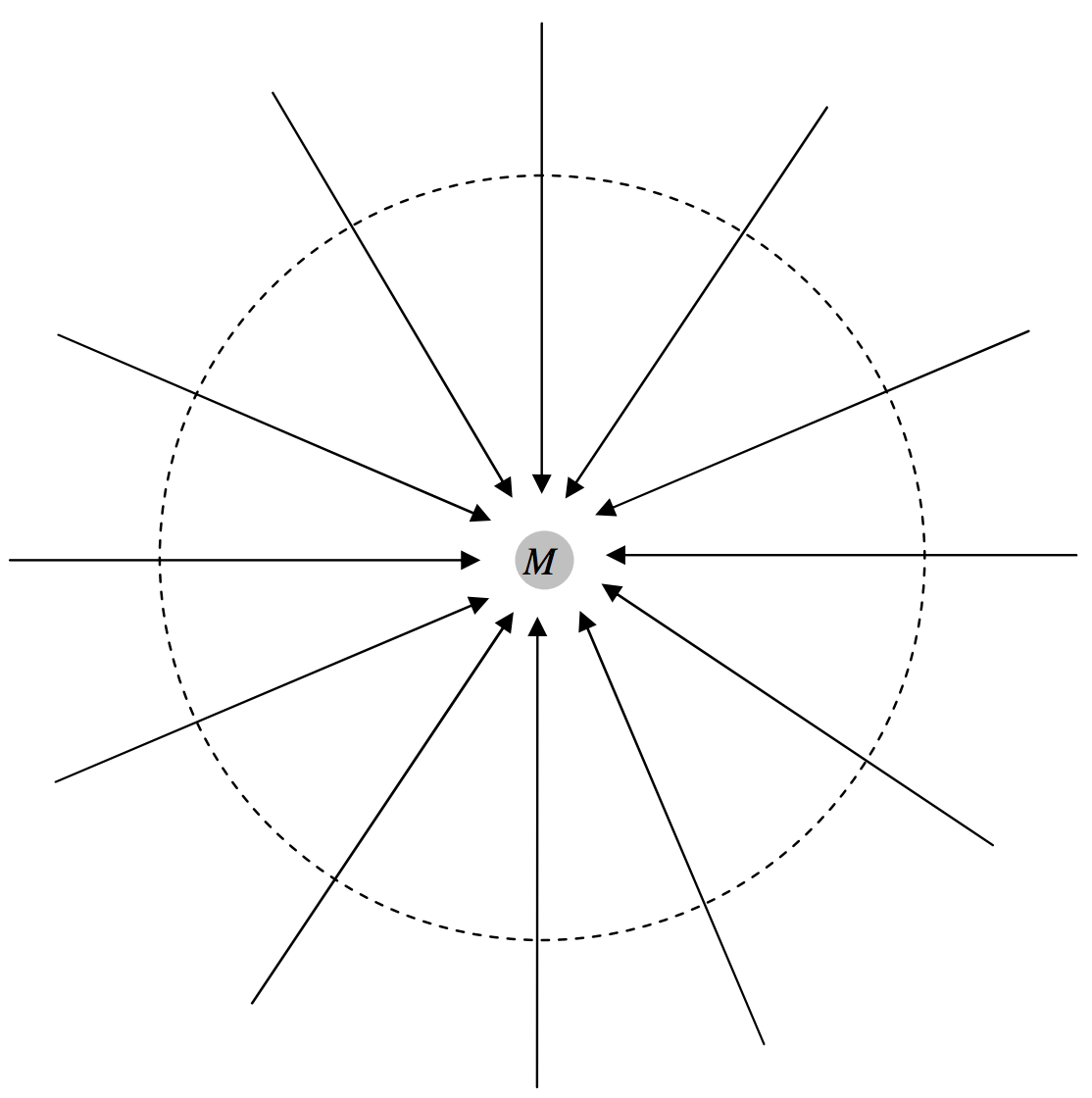
FIGURE V.14
The total normal outward gravitational flux through a closed surface is equal to −4πG times the total mass enclosed by the surface.
This is Gauss’s theorem.
Mathematically, the flux through the surface is expressed by the surface integral ∫∫g⋅dA. If there is a continuous distribution of matter inside the surface, of density ρ which varies from point to point and is a function of the coordinates, the total mass inside the surface is expressed by ∫∫∫ρdV. Thus Gauss’s theorem is expressed mathematically by
∫∫g⋅dA=−4πG∫∫∫ρdV.
You should check the dimensions of this Equation.
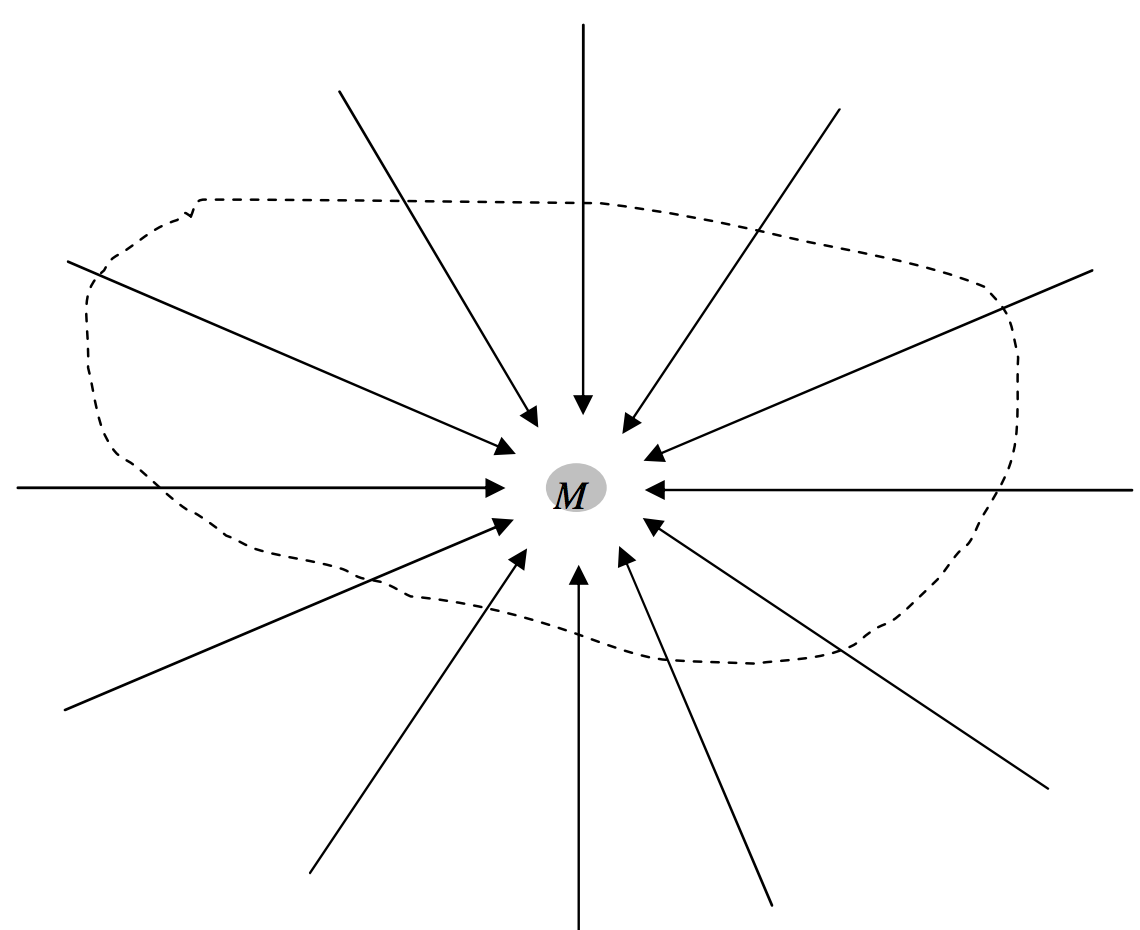
FIGURE V.15
In figure V.16 I have drawn gaussian spherical surfaces of radius r outside and inside hollow and solid spheres. In a and c, the outward flux through the surface is just −4πG times the enclosed mass M; the surface area of the gaussian surface is 4πr2. This the outward field at the gaussian surface (i.e. at a distance r from the centre of the sphere is −GM/r2. In b, no mass is inside the gaussian surface, and therefore the field is zero. In d, the mass inside the gaussian surface is Mr, and so the outward field is −GMr/r2.
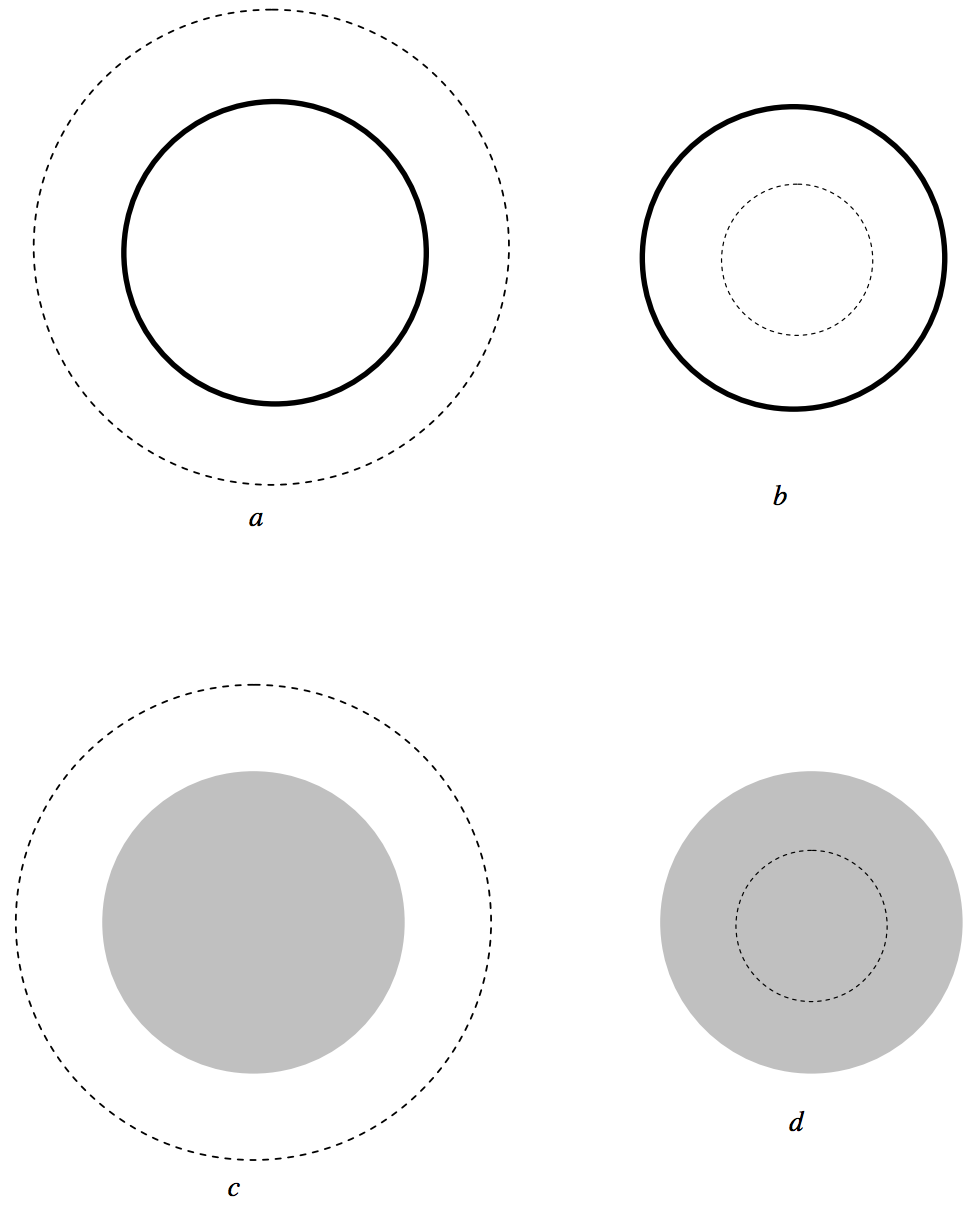
FIGURE V.16
In figure V.17 I draw (part of an) infinite rod of mass λ per unit length, and a cylindircal gaussian surface of radius h and length l around it.
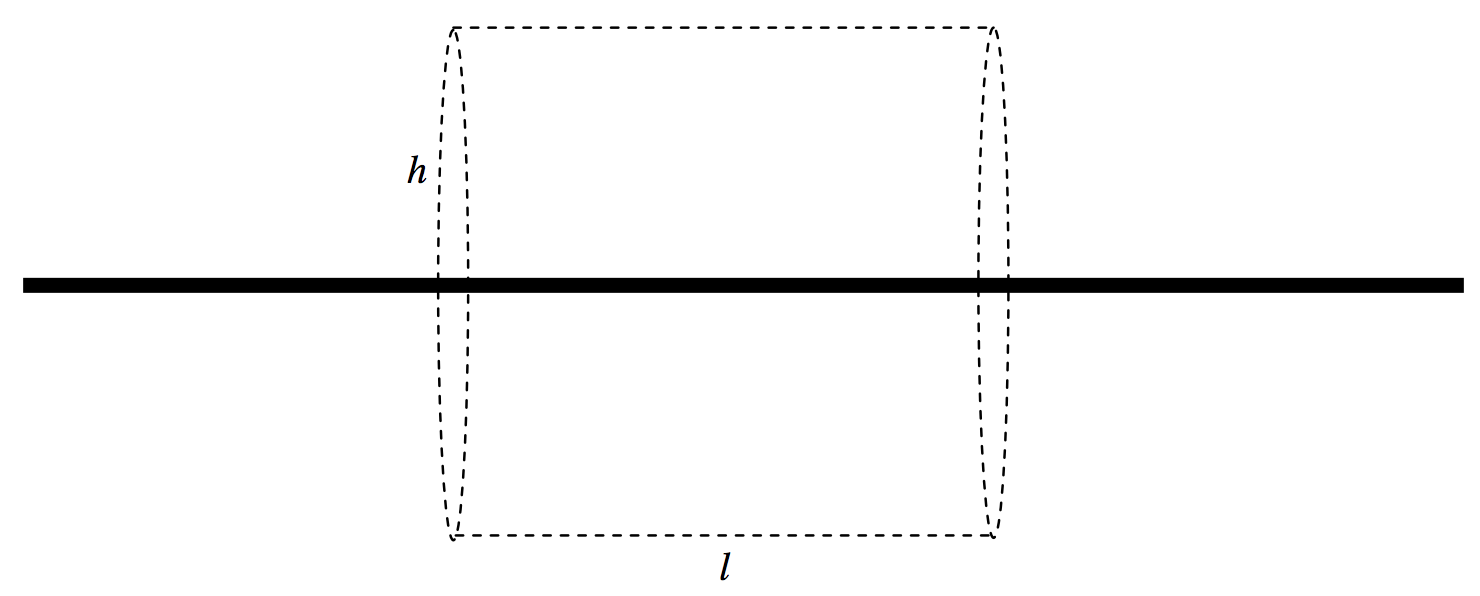
FIGURE V.17
The surface area of the curved surface of the cylinder is 2πhl, and the mass enclosed within it is λl. Thus the outward field at the surface of the gaussian cylinder (i.e. at a distance h from the rod) is −4πG×λl÷2πhl=−2Gλ/h, in agreement with Equation 5.4.18.
In figure V.18 I have drawn (part of) an infinite plane lamina of surface density σ, and a cylindrical gaussian surface or cross-sectional area A and height 2h.
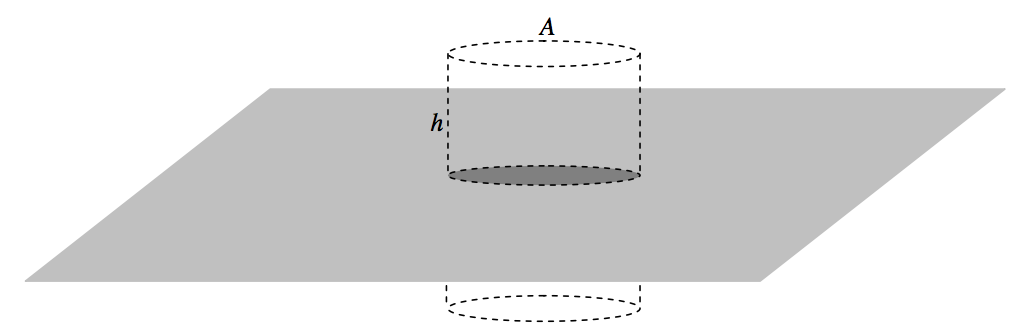
FIGURE V.18
The mass enclosed by the cylinder is σA and the area of the two ends of the cylinder is 2A. The outward field at the ends of the cylinder (i.e. at a distance h from the plane lamina) is therefore −4πG×σA÷2A=−2πGσ, in agreement with Equation 5.4.13.


