17.1: Introduction to Visual Binary Stars
( \newcommand{\kernel}{\mathrm{null}\,}\)
Many stars in the sky are seen through a telescope to be two stars apparently close together. By the use of a filar micrometer it is possible to measure the position of one star (the fainter of the two, for example) with respect to the other. The position is usually expressed as the angular distance ρ (in arcseconds) between the stars and the position angle θ of the fainter star with respect to the brighter. (The separation can be determined in kilometres rather than merely in arcseconds if the distance from Earth to the pair is known.) The position angle is measured counterclockwise from the direction to north. See figure XVII.1.
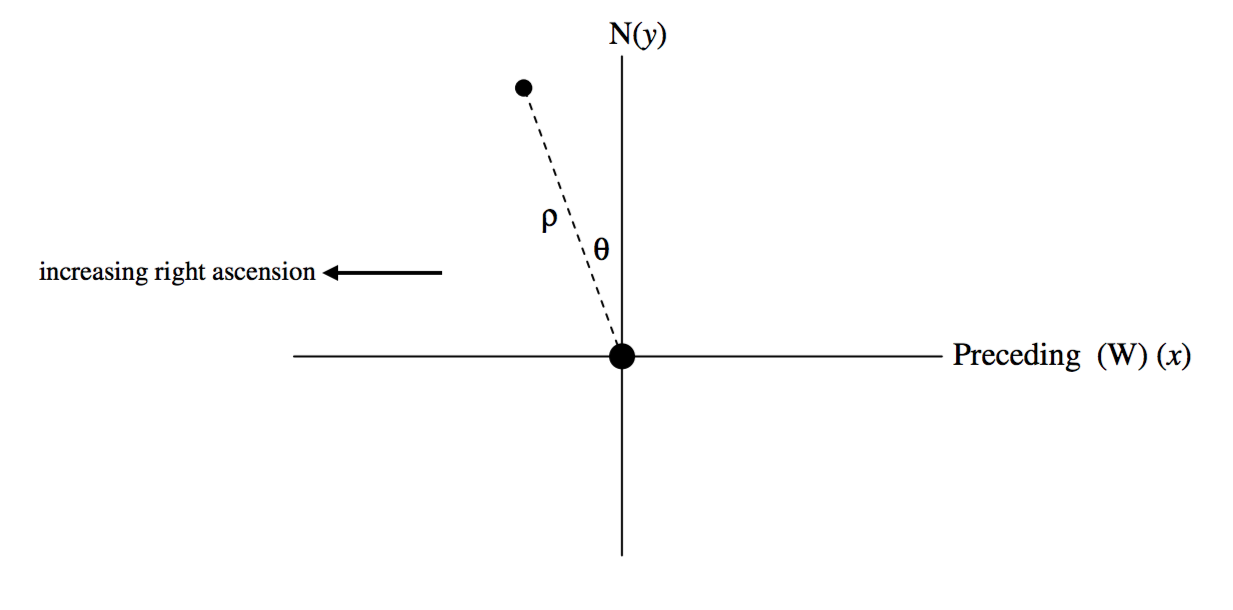
FIGURE XVII.1
These coordinates (ρ,θ) of one star with respect to the other can, of course, easily be converted to (x,y) coordinates. In any case, after the passage of many years (sometimes longer that the lifetime of an astronomer) one ends up with a table of coordinates as a function of time. Because the orbital period is typically of the order of many years, and the available observations are correspondingly spread out over a long period of time, it needs to be pointed out that all position angles, which are measured with respect to the equator of date, need to be adjusted so as to refer to a standard equator, such as that of J2000.0. I don’t wish to interrupt the flow of thought here by discussing this point (important though it is) in detail; suffice it to say that
θ2000.0=θt+20′′×(2000−t)sinαsecδ,
where t is the epoch of the observation in years, and the position angles are expressed in arcseconds.
If one star appears to move in a straight line with respect to the other, it is probable that the two stars are not physically connected but they just happen to lie almost in the same line of sight. Such a pair is called an optical pair or an optical double.
However, if one star appears to describe an ellipse relative to the other, then the two stars are physically connected and are moving around their common centre of mass.
The angular separation between the two stars is usually very small, of the order of arcseconds or less, and is not easy to measure. Much more difficult to measure would be the distances of the two stars individually from their mutual centre of mass. Close pairs are usually measured visually with a filar micrometer, and it is then almost invariably the case that what is measured is the position of the secondary with respect to the primary. Wider pairs, however, can be measured from photographs, or, today, from CCD images. In that case, not only are the measurements more precise, but it is possible to measure the position of each component with respect to background calibration stars, and hence to measure the position of each component with respect to the centre of mass of the system. This enables us to determine the mass ratio of the two components. Pairs that are sufficiently wide apart for photographic measurements, however, come with their own set of problems. If their angular separation is large, this could mean either that the real, linear separation in kilometres is large, or else that the stars are not very far from the Sun. In the former case, we may have to wait rather a long time (perhaps more than an average human lifetime) for the two stars to describe a complete orbit. In the latter case, we may have to take account of complications such as proper motion or annual parallax.
The brighter of the two stars is the primary, and the fainter is the secondary. This will nearly always mean (though not necessarily so) that the primary star is also the more massive of the pair, but this cannot be assumed without further evidence. If the two stars are of equal brightness, it is arbitrary which one is designated the primary. If the two stars are of equal brightness, it can sometimes happen that, when they become very close to each other, they merge and cannot be distinguished until their separation is sufficiently great for them to be resolved again. It may then not be obvious which of the two had been designated the “primary”.
The orbit of the secondary around the primary is, of course, a keplerian ellipse. But what one sees is the projection of this orbit on the “plane of the sky”. (The “plane of the sky” is the phrase almost universally used by observational astronomers, and there is no substantial objection to it; formally it means the tangent plane to the celestial sphere at the position of the primary component.) The projection of the true orbit on the plane of the sky is the apparent orbit, and both are ellipses. The centre of the true ellipse maps on to the centre of the apparent ellipse, but the foci of the true ellipse do not map on to the foci of the apparent ellipse. The primary star is at a focus of the true ellipse, but it is not at a focus of the apparent ellipse. The radius vector in the true orbit sweeps out equal areas in equal times, according to Kepler’s second law. In projection to the plane of the sky, all areas are reduced by the same factor (cosi). Consequently the radius vector in the apparent orbit also sweeps out equal areas in equal times, even though the primary star is not at a focus of the apparent ellipse.
Having secured the necessary observations over a long period of time, the astronomer faces two tasks. First the apparent orbit has to be determined; then the true orbit has to be determined.


