11.9: APPENDIX A- Evaluation of the Voigt Curve of Growth Integral
( \newcommand{\kernel}{\mathrm{null}\,}\)
We wish to evaluate the equivalent width as given by equation 11.6.2:
W=2∫∞0(1−exp{−Clτ(0)∫∞−∞exp[−(ξ−x)2ln2/g2]ξ2+l2dξ})dx.
We slightly simplify it by introducing dimensionless variables W′,x′,ξ′ and l′ defined by X′=Xcλ0Vm=X√ln2g, where X is any of W,x,ξ or l. That is, we are expressing lengths in units of g/√ln2. Then:
W′=2∫∞0(1−exp{−Cl′τ(0)∫∞−∞exp[−(ξ′−x′)2]ξ′2+l′2dξ′})dx′.
We shall eventually want to evaluate the integral as a function of the gaussian ratio kG, and we note that l′=(1kG−1)√ln2. Since ξ′ is a dummy variable, we could in principle dispense with the prime as superfluous, but it is probably helpful to retain the prime. The limits of the inner integral can be made finite by means of a change of variable. The substitution ξ′=l′tanθ will achieve this, but the introduction of a trigonometric function will increase the computing time. An alternative is ξ′=2l′t1−t2, which looks clumsier but is rather faster. The equation becomes
W′=2∫∞0(1−exp{−2Cτ(0)∫1−1exp[−(2l′t1−t2−x′)2]1+t2dt})dx′.
This integral is not particularly easy, and I do not advise merely putting it into a prepackaged integration program without critical examination. (Indeed I never advocate that!) One is faced with the usual problems of numerical integration: What should be the step size and number of steps? And, in the case of the outer integral, how far should we take the upper limit? One way to determine the necessary number of intervals (and step size) is to try, say 100 intervals, and then try 1000, and see if it makes any difference. Similarly with determining the upper limit to the outer integration, try integrating to x′=5, and then to 10, and see if it makes any difference. But this integral has some problems of its own.
Some insight into the problems can be obtained by looking at the behaviour of the inner integrand. This function, exp[−(2l′t1−t2−x′)2]1+t2, is shown as a function of t for four different values of x′ in figure XI.A1 The value of l′ for the figure is 1/(4π), which has no particular significance, since the figure is intended solely for illustrative purposes.
For x′=0, the function is symmetric about t=0, but not for other values of x′. For small values of x', there is no particular difficulty with the integration, either by Simpson’s rule or by seven-point integration (see my Web notes on Celestial Mechanics, Chapter 1).
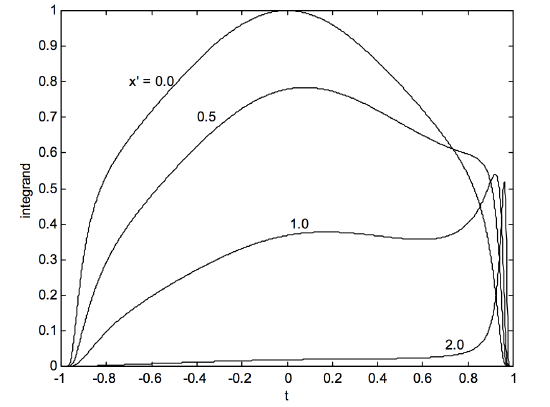
FIGURE XI.A1
However, for large x′, the integrand is close to zero for most of the range between t=−1.0 and 0.0, but, close to t=1.0, the integrand exhibits a sharp spike, becoming almost a delta-function for larger x′. A coarse interval for integration may miss the spike altogether, while a very fine interval will use massive amounts of computer time to no good purpose over most of the range of t. Fortunately, the area under the spike is progressively smaller and smaller for larger and larger x′ but the nagging question still remains, when may one stop integrating? One useful, efficient and effective technique is to adjust the size of the interval for integration according to the slope of the function. A coarse interval is quite adequate while the graph is near-horizontal, but a much finer integration step kicks in as soon as the slope becomes large. This requires a certain amount of programming legerdemain, but is frequently resorted to in such situations.
The part of equation 11.A 2:
exp{−Clτ(0)∫∞−∞exp[−(ξ−x)2ln2/g2]ξ2+l2dξ}
represents the optically thick Voigt profile. This is shown for l′=1/(4π) for several τ(0) in figure XI.A.2. The value l′=1/(4π) has no particular significance; figure XI.A.2 was drawn solely for illustrative purposes.
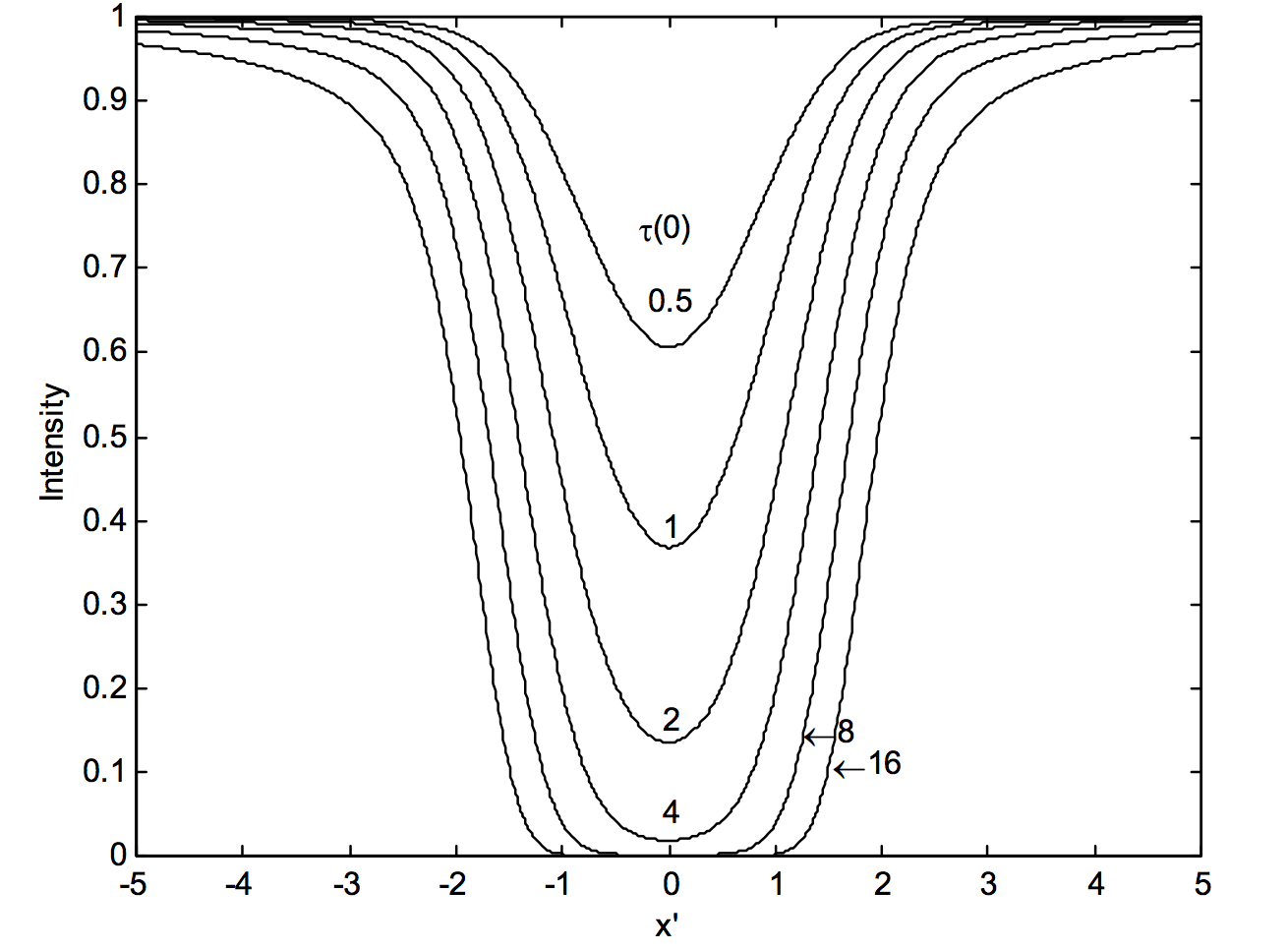
FIGURE XI.A2
The equivalent width (equation 11.A.1) is the area above these curves, and it can be seen again that determining the upper limit for x′ is a problem.
We can, however, remember that the profile that we are integrating is the convolution of a gaussian and a lorentzian, and that x′ is λ−λ0 in units of 2g/√ln2. The gaussian component has very small wings, whereas the lorentzian profile has extensive wings. The ratio of the gaussian component to the ordinate to the lorentzian component is (l′2+x′2l′2)exp(−x′2), where l′=(1/kG−1)√ln2. The value of x′ at which this ratio drops to 0.0001 is shown as a function of kG in figure XI.A.1a. Beyond this point one can treat the wings of the profile as lorentzian.
Thus equation 11.A.2 can be integrated by treating the optically thin profile as a Voigt function up to some x′=a and as a lorentzian function thereafter. That is, I have written equation 11.A.2 as
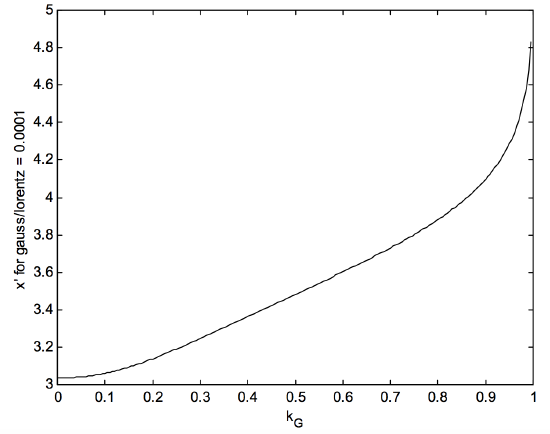
FIGURE XI.A.1A
W′=2∫a0(1−exp{−Cl′τ(0)∫∞−∞exp[−(ξ′−x′)2]ξ′2+l′2dξ′})dx′+2∫∞a(1−exp{−τ(0)x′2+l′2})dx′.
On substitution of ξ′=2l′t1−t2 in the first integral and x′=l′tanθ in the second, this becomes
W′=2∫a0(1−exp{−2Cτ(0)∫1−1exp[−(2l′t1−t2−x′)2]1+t2dt})dx′+2l′∫π/2α(1−exp{−τ(0)cos2θ})cos2θdθ,
where tanα=l′/a. The dreaded symbol ∞ has now gone and, further, there is no problem at the upper limit of the second integral, for the value of the integrand when θ=π/2 is unity.


