15: The Effect of a Tilt of the Orbital Plane

We are almost ready to take on a real, observed binary star orbit. However, there is one more factor we must be able to handle: a "tilt" of the orbital plane. By "tilt", I mean "tilt away from face-on to our line of sight." Astronomers use the term inclination to describe this variable, and define it so that

• inclination \(\mathbf{i = 0}\) means "face-on"
• inclination \(\mathbf{i = 90} \textbf{ degrees}\) means "edge-on"

The behavior of objects in a tilted orbit will NOT be exactly what we expect; for example, the radius vector joining the primary to the secondary star will NOT sweep out equal areas in equal times. Kepler's Third Law won't give the correct results, either. So, in order to derive the proper masses for stars in a binary system, we need to figure out this "tilt" so that we can remove it before calculating the masses.

Let's approach the problem in a gradual way. We'll start with something easy -- if you know the orientation of the TRUE orbit, what does the OBSERVED orbit look like? -- and work our way to the harder, inverse problem (which is what we really need to solve).

Tilting an orbit around its major axis

Suppose we start with a circular orbit.

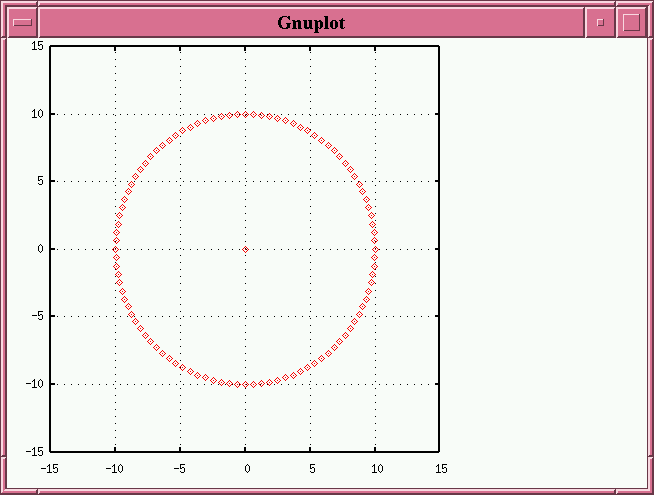
The primary star sits at the middle of the orbit, (0, 0), and the secondary star moves around it.

We'll pick the horizontal, x-axis as the axis around which we'll tilt this orbit. If we tilt it by 30 degrees, we see (true orbit in red, apparent orbit in green)

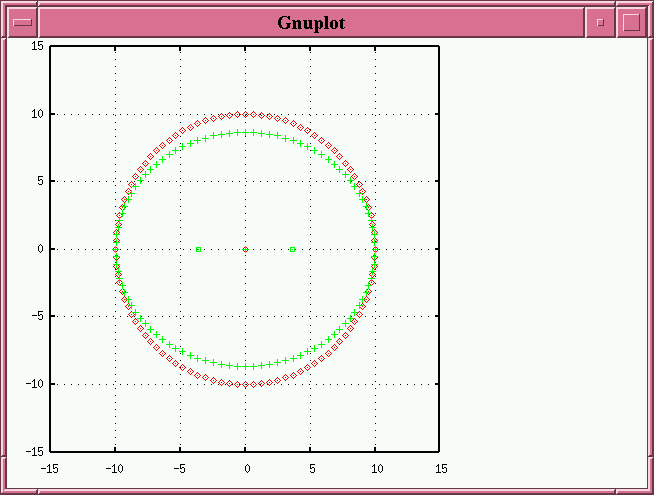
Note that the circle has become an ellipse -- no surprise there. The foci of this APPARENT ellipse are NOT at the position of the primary star, which still sits at the origin. The fact that the primary star is NOT at one of the foci is a signal to us that the orbit has been tilted.

On the other hand, suppose that we start with a truly elliptical orbit, with \(\mathbf{e = 0.8}\).

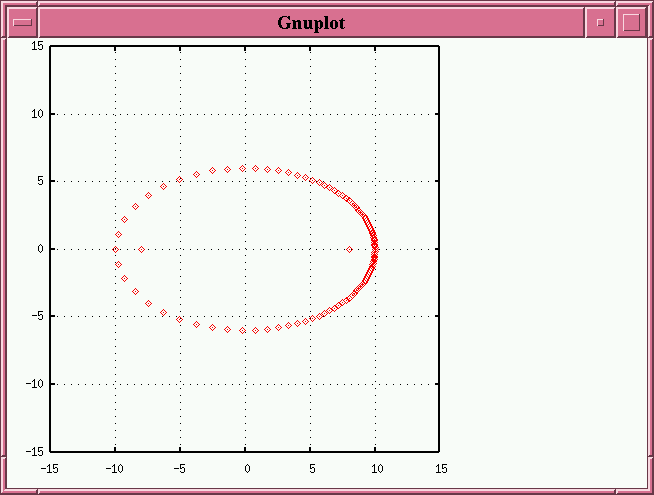
If we tilt it around its major axis (by 30 degrees in the example below), we make it even skinnier, and the apparent foci move even farther away from the center.

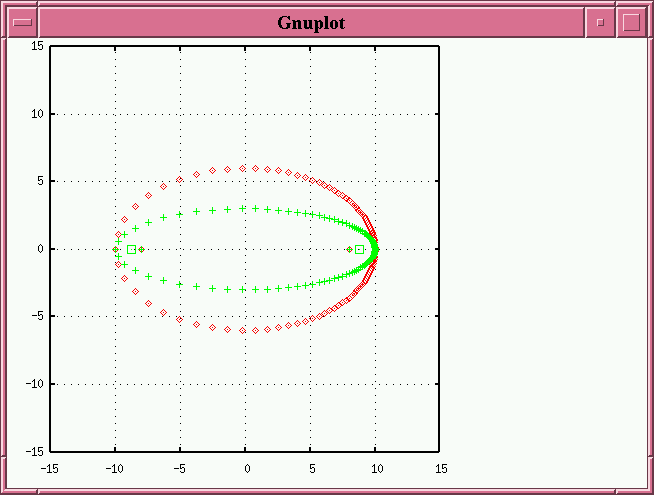
We can sum up this behavior as follows:

Rule 1: tilting an ellipse along its major axis

• makes it more skinny
• pushes the (new) foci out from the center

So, if we find an observed orbit in which the primary star lies WITHIN the observed foci, along the major axis, then the original orbit has been tilted along its major axis.

Tilting an orbit around its minor axis

We'll start with an elliptical orbit of true ellipticity \(\mathbf{e = 0.8}\) again.

If we tilt it slightly around its minor axis (by 30 degrees in the example below), we make it fatter. The apparent foci (green squares) now lie closer to the center of the ellipse than the actual primary star position (either of the projected true foci, shown as red crosses).

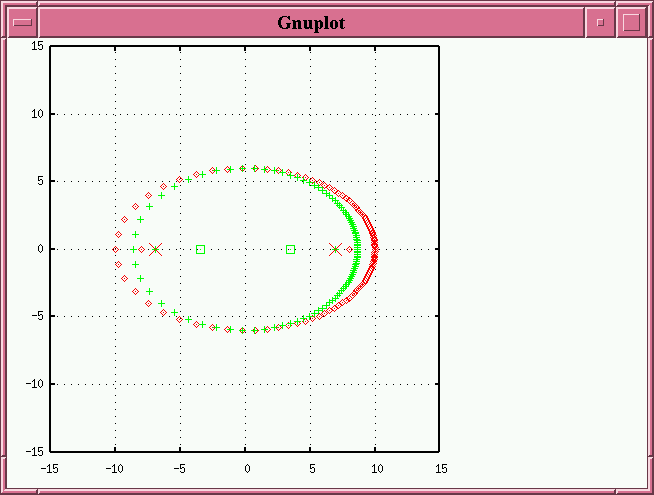
If we tilt it A LOT around its minor axis (by 60 degrees in the example below), we not only make it fatter, we rotate the apparent major axis by 90 degrees: what APPEARS to be the major axis is actually along the true orbit's minor axis. The apparent foci (green squares) now lie on a different axis than the actual primary star position (either of the projected true foci, shown as red crosses).

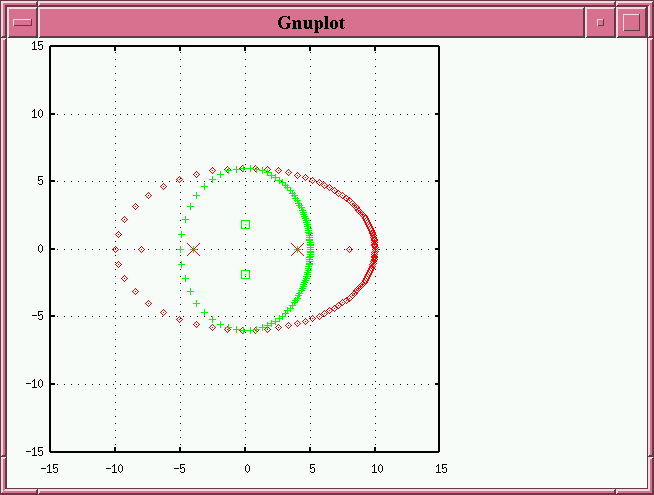
We can sum up this behavior as follows:

Rule 2: tilting an ellipse along its minor axis

• makes it fatter
• pulls the (new) foci inwards, towards the center
• eventually swaps the major and minor axes

Okay, so, if we see an orbit in which the primary star is located along either the major or minor axis of the apparent ellipse, we know what has happened. By tilting the apparent orbit BACK in the appropriate direction until the orbit's foci fall upon the primary star, we can recover the real orbit.

Tilting an orbit around some other axis

Things are more complicated if the primary star does NOT lie along either axis of the observed ellipse, as in the real case of Sirius:

What must have happened here is that the orbit is tilted, but around some axis (passing through the center of the true ellipse) which is neither the major nor the minor axis. Astronomer call this axis around which the orbit is tilted the line of nodes. Let's see what happens when the line of nodes doesn't lie along a principal axis.

We'll start with an elliptical orbit of true ellipticity \(\mathbf{e = 0.8}\) again.

Suppose we want to tilt it around an axis which is 30 degrees away from the major axis (in other words, the line of nodes is 30 degrees away from the major axis):

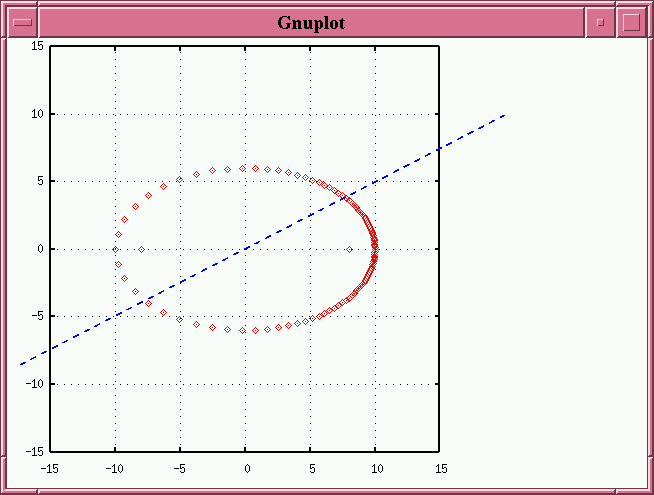
We can accomplish this in two steps:

1. create a copy of the original ellipse which is rotated by 30 degrees relative to the original ellipse

   

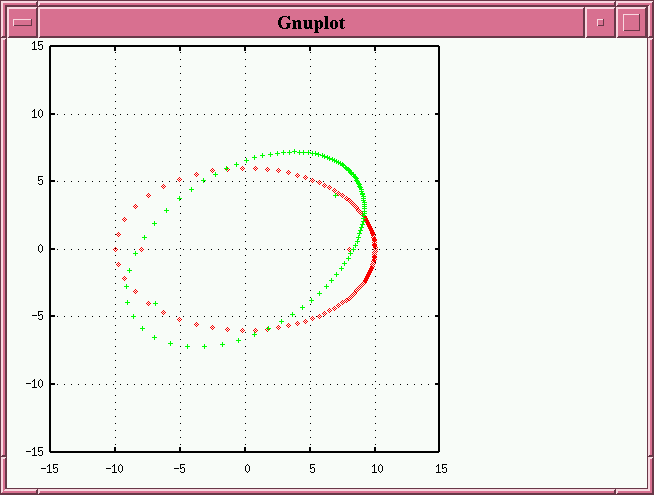
2. now, to perform the tilt, we project the copy around the x-axis: a point at \((x, y)\) goes to \((x, y\cdot cos(i))\), where \(\mathbf{i}\) is the angle of inclination. In this example, \(\mathbf{i = 60} \textbf{ degrees}\). This projection leaves the x-values alone, but pulls the y-values down towards the y-axis.

   

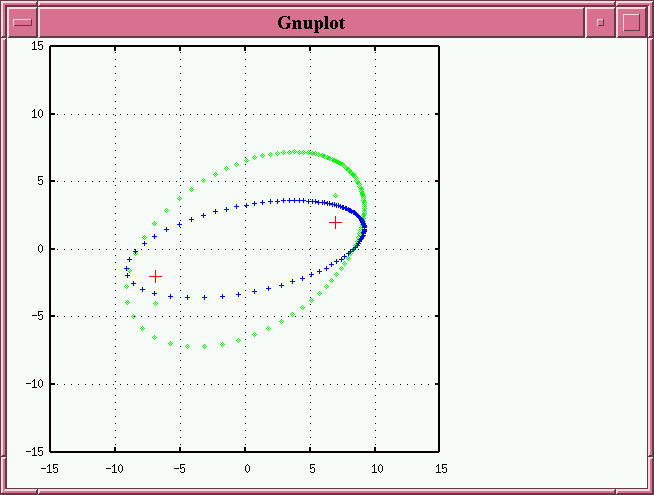
We end up with an observed orbit which looks like an ellipse, but the primary star is definitely NOT along either axis of this ellipse.

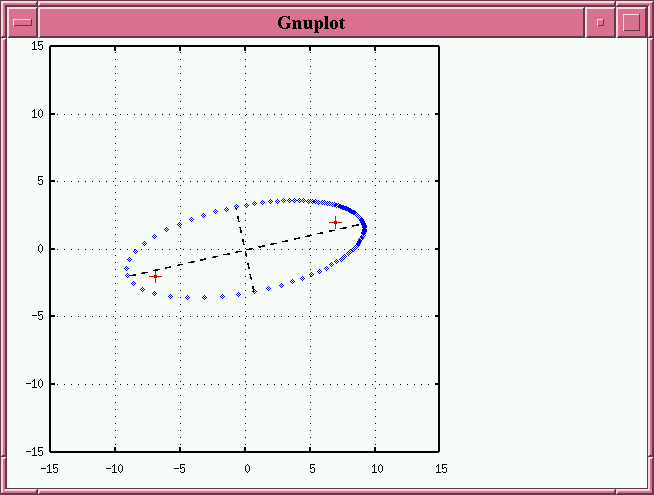
We can make the primary star move even further away from the apparent major axis by

• rotating the line of nodes further from the original major axis (in the example below, by 60 degrees, followed by a 60-degree tilt)

  

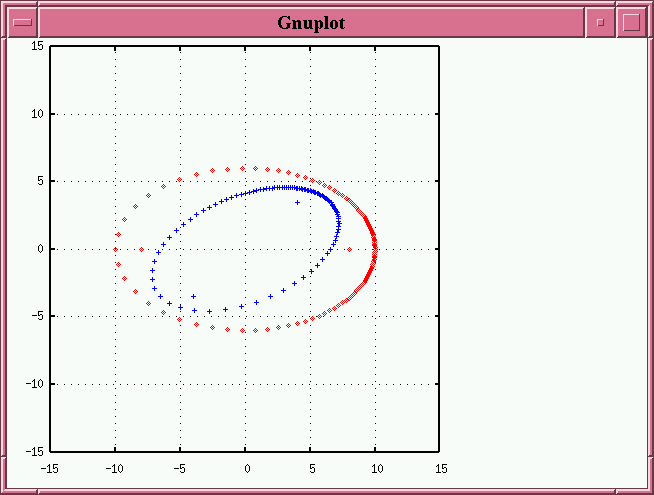
  or even farther from the original major axis (in the example below, by 80 degrees, followed by a 60-degree tilt)

  

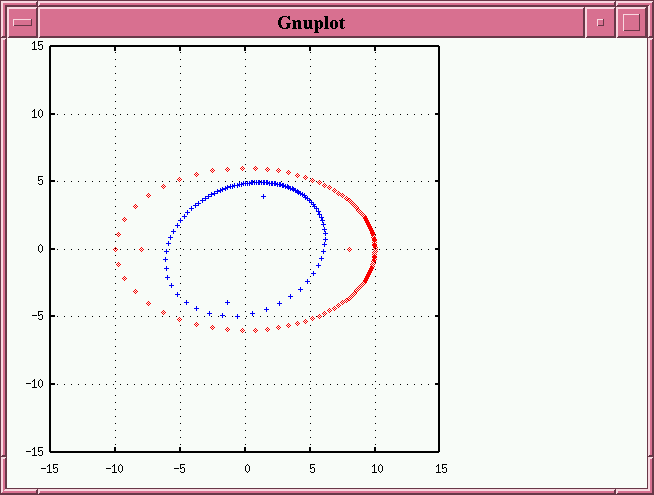
• making the tilt angle larger (in the example below, we rotate by only 30 degrees, but then tilt by 80-degrees)

  

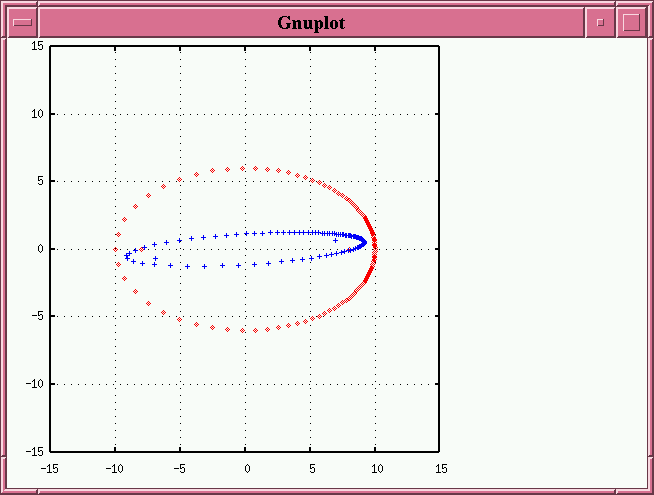
The big question is: can we come up with some simple rules, based upon the location of the primary star in the apparent orbit, which tell us how to un-tilt the apparent orbit to recover the original ellipse? Note that there are 2 degrees of freedom:

• the angle of the line of nodes away from the major axis of the true ellipse
• the inclination angle \(\mathbf{i}\) by which we tilt the true ellipse around the line of nodes

The brute-force approach

There is one technique we can try which doesn't require any rules at all. It wasn't available to the classical astronomers of the eighteenth and nineteenth centuries, but that's okay: if it works, it works. This is the brute-force approach.

When you are handed an observed orbit which is clearly the result of some tilt not along a principal axis (i.e. when you see the primary star lie off the major and minor axes), like this:

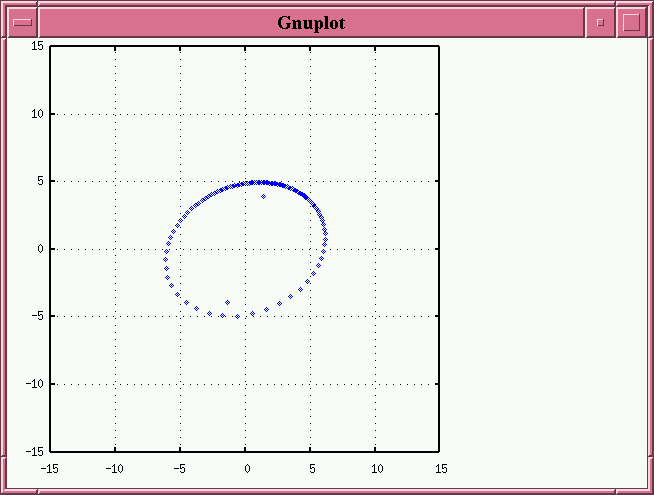
then you can pull out your computer and ask it to repeat a series of calculations over and over again:

1. start with measurements \((r, θ)\) of the secondary star relative to the primary star
2. pick a coordinate system so that the x-axis lies along the major axis of the orbit, and the y-axis along the minor axis
3. compute \((x, y)\) positions of each point along the ellipse, and the \((x, y)\) position of the primary star
4. LOOP1: select some line -- a guess at the line of nodes -- which passes through the center of the observed ellipse at an angle \(\mathbf{φ}\) relative to the x-axis
   1. compute positions \((x', y')\) based on a set of coordinate axes rotated by angle \(\mathbf{φ}\) relative to the original axes
   2. LOOP2: select some tilt angle \(\mathbf{i}\)
      1. correct all \((x', y')\) positions for a tilt of angle i around the axis defined by the line; call the tilted positions \((x'', y'')\)
      2. find the parameters of the new ellipse made by these corrected positions \((x'', y'')\)
      3. figure out the position of the foci of the new ellipse
      4. compute the distance between the foci and the corrected position of the primary star

The combination of axis angle \(\mathbf{φ}\) and inclination angle \(\mathbf{i}\) which brings the primary star closest to a corrected focus is the one to choose. This is not an elegant technique, but it must produce at least one reasonably good result. Of course, it's possible (due to measurement errors) that it might produce several combinations of rotation angle and tilt which yield equally good positions of corrected focus. In that case, you may use the range of angles and tilts to estimate the uncertainty in your result.

Exercises

• Write down the equation(s) necessary to carry out step 2 in the procedure above
• Write down the equation(s) necessary to carry out step 3a in the procedure above
• Write down the equation(s) necessary to carry out step 3b,i in the procedure above