2.2: Ancient Astronomy
- Page ID
- 3617
Learning Objectives
By the end of this section, you will be able to:
- Describe early examples of astronomy around the world
- Explain how Greek astronomers were able to deduce that Earth is spherical
- Explain how Greek astronomers were able to calculate Earth’s size
- Describe the motion of Earth called precession
- Describe Ptolemy’s geocentric system of planetary motion
Let us now look briefly back into history. Much of modern Western civilization is derived in one way or another from the ideas of the ancient Greeks and Romans, and this is true in astronomy as well. However, many other ancient cultures also developed sophisticated systems for observing and interpreting the sky.
Astronomy around the World
Ancient Babylonian, Assyrian, and Egyptian astronomers knew the approximate length of the year. The Egyptians of 3000 years ago, for example, adopted a calendar based on a 365-day year. They kept careful track of the rising time of the bright star Sirius in the predawn sky, which has a yearly cycle that corresponded with the flooding of the Nile River. The Chinese also had a working calendar; they determined the length of the year at about the same time as the Egyptians. The Chinese also recorded comets, bright meteors, and dark spots on the Sun. (Many types of astronomical objects were introduced in Science and the Universe: A Brief Tour. If you are not familiar with terms like comets and meteors, you may want to review that chapter.) Later, Chinese astronomers kept careful records of “guest stars”—those that are normally too faint to see but suddenly flare up to become visible to the unaided eye for a few weeks or months. We still use some of these records in studying stars that exploded a long time ago.
The Mayan culture in Mexico and Central America developed a sophisticated calendar based on the planet Venus, and they made astronomical observations from sites dedicated to this purpose a thousand years ago. The Polynesians learned to navigate by the stars over hundreds of kilometers of open ocean—a skill that enabled them to colonize new islands far away from where they began.
In Britain, before the widespread use of writing, ancient people used stones to keep track of the motions of the Sun and Moon. We still find some of the great stone circles they built for this purpose, dating from as far back as 2800 BCE. The best known of these is Stonehenge, which is discussed in Earth, Moon, and Sky.
Early Greek and Roman Cosmology
Our concept of the cosmos—its basic structure and origin—is called cosmology, a word with Greek roots. Before the invention of telescopes, humans had to depend on the simple evidence of their senses for a picture of the universe. The ancients developed cosmologies that combined their direct view of the heavens with a rich variety of philosophical and religious symbolism.
At least 2000 years before Columbus, educated people in the eastern Mediterranean region knew Earth was round. Belief in a spherical Earth may have stemmed from the time of Pythagoras, a philosopher and mathematician who lived 2500 years ago. He believed circles and spheres to be “perfect forms” and suggested that Earth should therefore be a sphere. As evidence that the gods liked spheres, the Greeks cited the fact that the Moon is a sphere, using evidence we describe later.
The writings of Aristotle (384–322 BCE), the tutor of Alexander the Great, summarize many of the ideas of his day. They describe how the progression of the Moon’s phases—its apparent changing shape—results from our seeing different portions of the Moon’s sunlit hemisphere as the month goes by (see Earth, Moon, and Sky). Aristotle also knew that the Sun has to be farther away from Earth than is the Moon because occasionally the Moon passed exactly between Earth and the Sun and hid the Sun temporarily from view. We call this a solar eclipse.
Aristotle cited convincing arguments that Earth must be round. First is the fact that as the Moon enters or emerges from Earth’s shadow during an eclipse of the Moon, the shape of the shadow seen on the Moon is always round (Figure \(\PageIndex{1}\)). Only a spherical object always produces a round shadow. If Earth were a disk, for example, there would be some occasions when the sunlight would strike it edge-on and its shadow on the Moon would be a line.

As a second argument, Aristotle explained that travelers who go south a significant distance are able to observe stars that are not visible farther north. And the height of the North Star—the star nearest the north celestial pole—decreases as a traveler moves south. On a flat Earth, everyone would see the same stars overhead. The only possible explanation is that the traveler must have moved over a curved surface on Earth, showing stars from a different angle. (See the How Do We Know Earth Is Round? feature for more ideas on proving Earth is round.)
One Greek thinker, Aristarchus of Samos (310–230 BCE), even suggested that Earth was moving around the Sun, but Aristotle and most of the ancient Greek scholars rejected this idea. One of the reasons for their conclusion was the thought that if Earth moved about the Sun, they would be observing the stars from different places along Earth’s orbit. As Earth moved along, nearby stars should shift their positions in the sky relative to more distant stars. In a similar way, we see foreground objects appear to move against a more distant background whenever we are in motion. When we ride on a train, the trees in the foreground appear to shift their position relative to distant hills as the train rolls by. Unconsciously, we use this phenomenon all of the time to estimate distances around us.
The apparent shift in the direction of an object as a result of the motion of the observer is called parallax. We call the shift in the apparent direction of a star due to Earth’s orbital motion stellar parallax. The Greeks made dedicated efforts to observe stellar parallax, even enlisting the aid of Greek soldiers with the clearest vision, but to no avail. The brighter (and presumably nearer) stars just did not seem to shift as the Greeks observed them in the spring and then again in the fall (when Earth is on the opposite side of the Sun).
This meant either that Earth was not moving or that the stars had to be so tremendously far away that the parallax shift was immeasurably small. A cosmos of such enormous extent required a leap of imagination that most ancient philosophers were not prepared to make, so they retreated to the safety of the Earth-centered view, which would dominate Western thinking for nearly two millennia.
HOW DO WE KNOW EARTH IS ROUND?
In addition to the two ways (from Aristotle’s writings) discussed in this chapter, you might also reason as follows:
- Let’s watch a ship leave its port and sail into the distance on a clear day. On a flat Earth, we would just see the ship get smaller and smaller as it sails away. But this isn’t what we actually observe. Instead, ships sink below the horizon, with the hull disappearing first and the mast remaining visible for a while longer. Eventually, only the top of the mast can be seen as the ship sails around the curvature of Earth. Finally, the ship disappears under the horizon.
- The International Space Station circles Earth once every 90 minutes or so. Photographs taken from the shuttle and other satellites show that Earth is round from every perspective.
- Suppose you made a friend in each time zone of Earth. You call all of them at the same hour and ask, “Where is the Sun?” On a flat Earth, each caller would give you roughly the same answer. But on a round Earth you would find that, for some friends, the Sun would be high in the sky whereas for others it would be rising, setting, or completely out of sight (and this last group of friends would be upset with you for waking them up).
Measurement of Earth by Eratosthenes
The Greeks not only knew Earth was round, but also they were able to measure its size. The first fairly accurate determination of Earth’s diameter was made in about 200 BCE by Eratosthenes (276–194 BCE), a Greek living in Alexandria, Egypt. His method was a geometric one, based on observations of the Sun.
The Sun is so distant from us that all the light rays that strike our planet approach us along essentially parallel lines. To see why, look at Figure \(\PageIndex{2}\). Take a source of light near Earth—say, at position A. Its rays strike different parts of Earth along diverging paths. From a light source at B, or at C (which is still farther away), the angle between rays that strike opposite parts of Earth is smaller. The more distant the source, the smaller the angle between the rays. For a source infinitely distant, the rays travel along parallel lines.
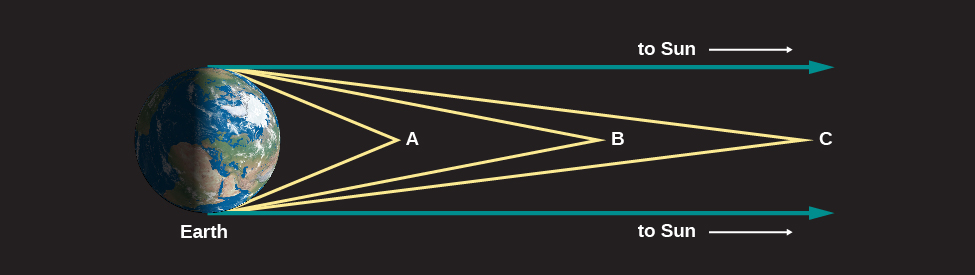
Of course, the Sun is not infinitely far away, but given its distance of 150 million kilometers, light rays striking Earth from a point on the Sun diverge from one another by an angle far too small to be observed with the unaided eye. As a consequence, if people all over Earth who could see the Sun were to point at it, their fingers would, essentially, all be parallel to one another. (The same is also true for the planets and stars—an idea we will use in our discussion of how telescopes work.)
Eratosthenes was told that on the first day of summer at Syene, Egypt (near modern Aswan), sunlight struck the bottom of a vertical well at noon. This indicated that the Sun was directly over the well—meaning that Syene was on a direct line from the center of Earth to the Sun. At the corresponding time and date in Alexandria, Eratosthenes observed the shadow a column made and saw that the Sun was not directly overhead, but was slightly south of the zenith, so that its rays made an angle with the vertical equal to about 1/50 of a circle (7°). Because the Sun’s rays striking the two cities are parallel to one another, why would the two rays not make the same angle with Earth’s surface? Eratosthenes reasoned that the curvature of the round Earth meant that “straight up” was not the same in the two cities. And the measurement of the angle in Alexandria, he realized, allowed him to figure out the size of Earth. Alexandria, he saw, must be 1/50 of Earth’s circumference north of Syene (Figure \(\PageIndex{3}\)). Alexandria had been measured to be 5000 stadia north of Syene. (The stadium was a Greek unit of length, derived from the length of the racetrack in a stadium.) Eratosthenes thus found that Earth’s circumference must be 50 × 5000, or 250,000 stadia.
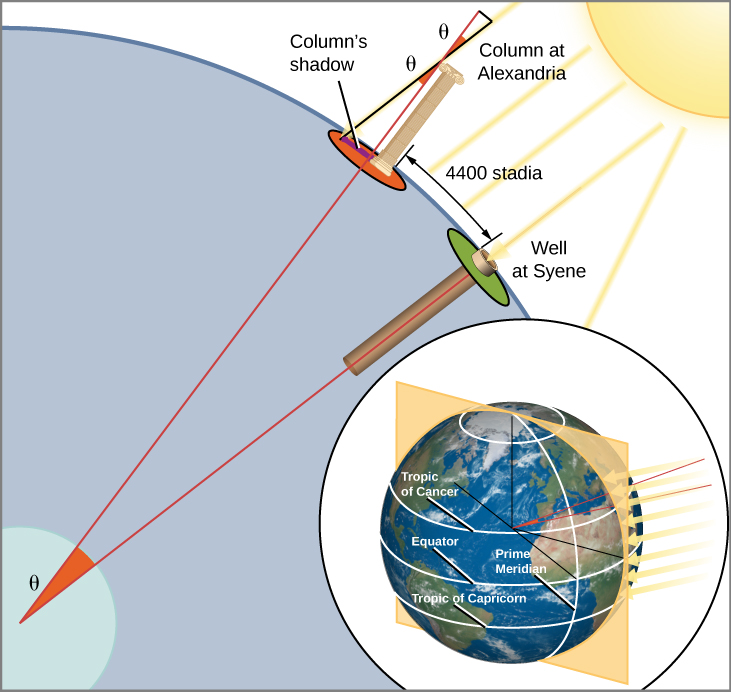
It is not possible to evaluate precisely the accuracy of Eratosthenes solution because there is doubt about which of the various kinds of Greek stadia he used as his unit of distance. If it was the common Olympic stadium, his result is about 20% too large. According to another interpretation, he used a stadium equal to about 1/6 kilometer, in which case his figure was within 1% of the correct value of 40,000 kilometers. Even if his measurement was not exact, his success at measuring the size of our planet by using only shadows, sunlight, and the power of human thought was one of the greatest intellectual achievements in history.
Hipparchus and Precession
Perhaps the greatest astronomer of antiquity was Hipparchus, born in Nicaea in what is present-day Turkey. He erected an observatory on the island of Rhodes around 150 BCE, when the Roman Republic was expanding its influence throughout the Mediterranean region. There he measured, as accurately as possible, the positions of objects in the sky, compiling a pioneering star catalog with about 850 entries. He designated celestial coordinates for each star, specifying its position in the sky, just as we specify the position of a point on Earth by giving its latitude and longitude.
He also divided the stars into apparent magnitudes according to their apparent brightness. He called the brightest ones “stars of the first magnitude”; the next brightest group, “stars of the second magnitude”; and so forth. This rather arbitrary system, in modified form, still remains in use today (although it is less and less useful for professional astronomers).
By observing the stars and comparing his data with older observations, Hipparchus made one of his most remarkable discoveries: the position in the sky of the north celestial pole had altered over the previous century and a half. Hipparchus deduced correctly that this had happened not only during the period covered by his observations, but was in fact happening all the time: the direction around which the sky appears to rotate changes slowly but continuously. Recall from the section on celestial poles and the celestial equator that the north celestial pole is just the projection of Earth’s North Pole into the sky. If the north celestial pole is wobbling around, then Earth itself must be doing the wobbling. Today, we understand that the direction in which Earth’s axis points does indeed change slowly but regularly—a motion we call precession. If you have ever watched a spinning top wobble, you observed a similar kind of motion. The top’s axis describes a path in the shape of a cone, as Earth’s gravity tries to topple it (Figure \(\PageIndex{4}\)).
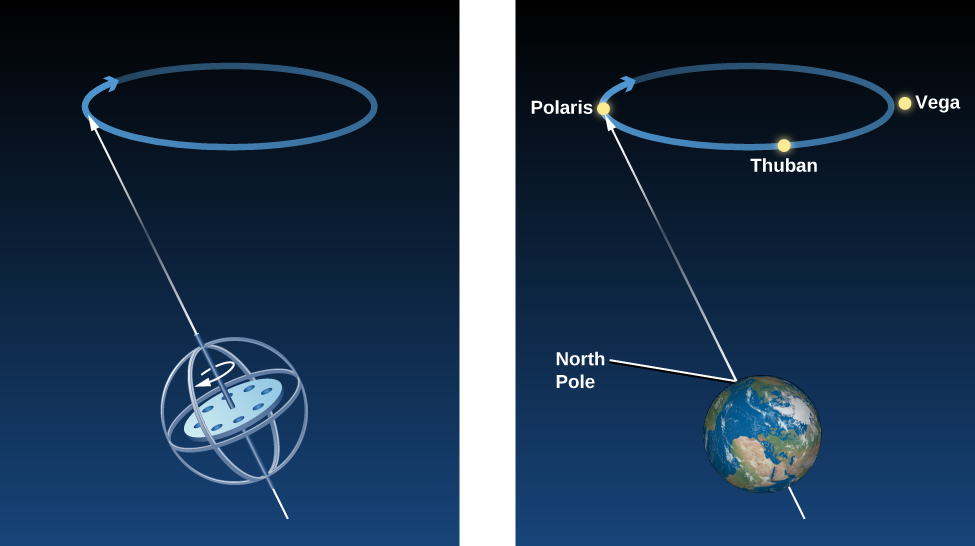
Because our planet is not an exact sphere, but bulges a bit at the equator, the pulls of the Sun and Moon cause it to wobble like a top. It takes about 26,000 years for Earth’s axis to complete one circle of precession. As a result of this motion, the point where our axis points in the sky changes as time goes on. While Polaris is the star closest to the north celestial pole today (it will reach its closest point around the year 2100), the star Vega in the constellation of Lyra will be the North Star in 14,000 years.
Ptolemy’s Model of the Solar System
The last great astronomer of the Roman era was Claudius Ptolemy (or Ptolemaeus), who flourished in Alexandria in about the year 140. He wrote a mammoth compilation of astronomical knowledge, which today is called by its Arabic name, Almagest (meaning “The Greatest”). Almagest does not deal exclusively with Ptolemy’s own work; it includes a discussion of the astronomical achievements of the past, principally those of Hipparchus. Today, it is our main source of information about the work of Hipparchus and other Greek astronomers.
Ptolemy’s most important contribution was a geometric representation of the solar system that predicted the positions of the planets for any desired date and time. Hipparchus, not having enough data on hand to solve the problem himself, had instead amassed observational material for posterity to use. Ptolemy supplemented this material with new observations of his own and produced a cosmological model that endured more than a thousand years, until the time of Copernicus.
The complicating factor in explaining the motions of the planets is that their apparent wandering in the sky results from the combination of their own motions with Earth’s orbital revolution. As we watch the planets from our vantage point on the moving Earth, it is a little like watching a car race while you are competing in it. Sometimes opponents’ cars pass you, but at other times you pass them, making them appear to move backward for a while with respect to you.
Figure \(\PageIndex{5}\) shows the motion of Earth and a planet farther from the Sun—in this case, Mars. Earth travels around the Sun in the same direction as the other planet and in nearly the same plane, but its orbital speed is faster. As a result, it overtakes the planet periodically, like a faster race car on the inside track. The figure shows where we see the planet in the sky at different times. The path of the planet among the stars is illustrated in the star field on the right side of the figure.
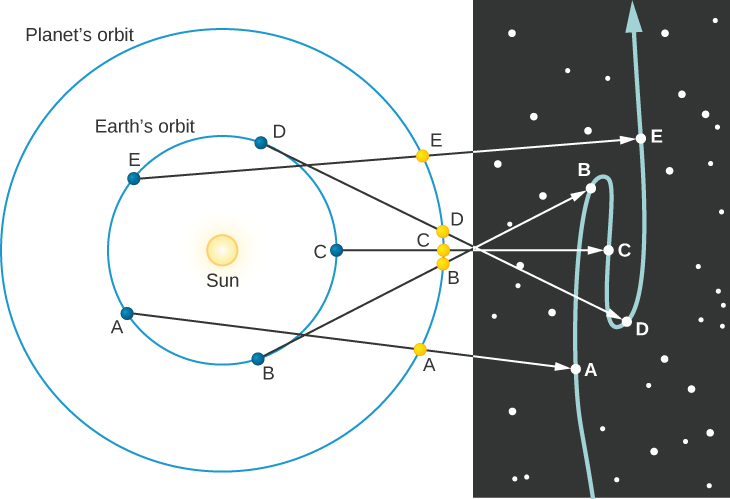
Figure \(\PageIndex{5}\) Retrograde Motion of a Planet beyond Earth’s Orbit. The letters on the diagram show where Earth and Mars are at different times. By following the lines from each Earth position through each corresponding Mars position, you can see how the retrograde path of Mars looks against the background stars.
Retrograde Motion
This retrograde simulation of Mars illustrates the motion of Mars as seen from Earth as well as Earth’s retrograde motion as seen from Mars. There is also an animation of the movement of the two planets relative to each other that creates the appearance of this motion.
Normally, planets move eastward in the sky over the weeks and months as they orbit the Sun, but from positions B to D in Figure \(\PageIndex{5}\), as Earth passes the planets in our example, it appears to drift backward, moving west in the sky. Even though it is actually moving to the east, the faster-moving Earth has overtaken it and seems, from our perspective, to be leaving it behind. As Earth rounds its orbit toward position E, the planet again takes up its apparent eastward motion in the sky. The temporary apparent westward motion of a planet as Earth swings between it and the Sun is called retrograde motion. Such backward motion is much easier for us to understand today, now that we know Earth is one of the moving planets and not the unmoving center of all creation. But Ptolemy was faced with the far more complex problem of explaining such motion while assuming a stationary Earth.
Furthermore, because the Greeks believed that celestial motions had to be circles, Ptolemy had to construct his model using circles alone. To do it, he needed dozens of circles, some moving around other circles, in a complex structure that makes a modern viewer dizzy. But we must not let our modern judgment cloud our admiration for Ptolemy’s achievement. In his day, a complex universe centered on Earth was perfectly reasonable and, in its own way, quite beautiful. However, as Alfonso X, the King of Castile, was reported to have said after having the Ptolemaic system of planet motions explained to him, “If the Lord Almighty had consulted me before embarking upon Creation, I should have recommended something simpler.”
Ptolemy solved the problem of explaining the observed motions of planets by having each planet revolve in a small orbit called an epicycle. The center of the epicycle then revolved about Earth on a circle called a deferent (Figure \(\PageIndex{6}\)). When the planet is at position x in Figure \(\PageIndex{6}\) on the epicycle orbit, it is moving in the same direction as the center of the epicycle; from Earth, the planet appears to be moving eastward. When the planet is at y, however, its motion is in the direction opposite to the motion of the epicycle’s center around Earth. By choosing the right combination of speeds and distances, Ptolemy succeeded in having the planet moving westward at the correct speed and for the correct interval of time, thus replicating retrograde motion with his model.
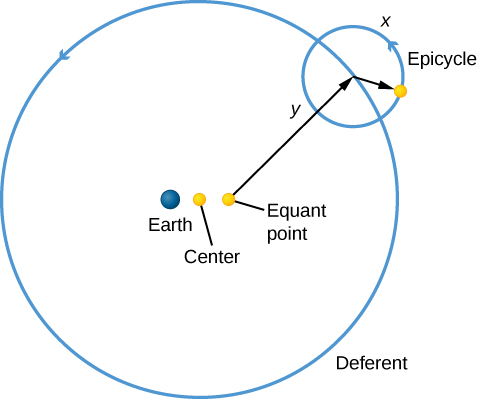
However, we shall see in Orbits and Gravity that the planets, like Earth, travel about the Sun in orbits that are ellipses, not circles. Their actual behavior cannot be represented accurately by a scheme of uniform circular motions. In order to match the observed motions of the planets, Ptolemy had to center the deferent circles, not on Earth, but at points some distance from Earth. In addition, he introduced uniform circular motion around yet another axis, called the equant point. All of these considerably complicated his scheme.
It is a tribute to the genius of Ptolemy as a mathematician that he was able to develop such a complex system to account successfully for the observations of planets. It may be that Ptolemy did not intend for his cosmological model to describe reality, but merely to serve as a mathematical representation that allowed him to predict the positions of the planets at any time. Whatever his thinking, his model, with some modifications, was eventually accepted as authoritative in the Muslim world and (later) in Christian Europe.
Summary
Ancient Greeks such as Aristotle recognized that Earth and the Moon are spheres, and understood the phases of the Moon, but because of their inability to detect stellar parallax, they rejected the idea that Earth moves. Eratosthenes measured the size of Earth with surprising precision. Hipparchus carried out many astronomical observations, making a star catalog, defining the system of stellar magnitudes, and discovering precession from the apparent shift in the position of the north celestial pole. Ptolemy of Alexandria summarized classic astronomy in his Almagest; he explained planetary motions, including retrograde motion, with remarkably good accuracy using a model centered on Earth. This geocentric model, based on combinations of uniform circular motion using epicycles, was accepted as authority for more than a thousand years.
Glossary
- apparent magnitude
- a measure of how bright a star looks in the sky; the larger the number, the dimmer the star appears to us
- cosmology
- the study of the organization and evolution of the universe
- epicycle
- the circular orbit of a body in the Ptolemaic system, the center of which revolves about another circle (the deferent)
- parallax
- the apparent displacement of a nearby star that results from the motion of Earth around the Sun
- precession (of Earth)
- the slow, conical motion of Earth’s axis of rotation caused principally by the gravitational pull of the Moon and Sun on Earth’s equatorial bulge
- retrograde motion
- the apparent westward motion of a planet on the celestial sphere or with respect to the stars


