5.8.9: Solid Sphere
( \newcommand{\kernel}{\mathrm{null}\,}\)
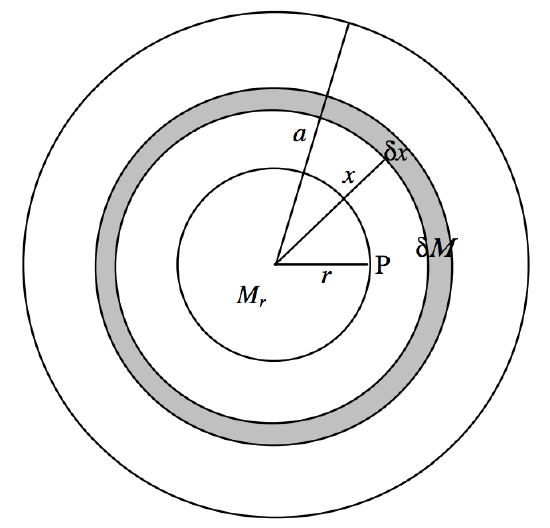
FIGURE V.24A
The potential outside a solid sphere is just the same as if all the mass were concentrated at a point in the centre. This is so, even if the density is not uniform, and long as it is spherically distributed. We are going to find the potential at a point P inside a uniform sphere of radius a, mass M, density ρ, at a distance r from the centre (r<a). We can do this in two parts. First, there is the potential from that part of the sphere “below” P. This is −GMr/r, where Mr=r3Ma3 is the mass within radius r. Now we need to deal with the material “above” P. Consider a spherical shell of radii x, x+δx. Its mass is δM=4πx2δx43πa3⋅M=3Mx2δxa3. The potential from this shell is −GδM/x=−3GMxδxa3. This is to be integrated from x=0 to a, and we must then add the contribution from the material “below” P. The final result is
ψ=−GM2a3(3a2−r2).
Figure V.25 shows the potential both inside and outside a uniform solid sphere. The potential is in units of −GM/r, and distance is in units of a, the radius of the sphere.
FIGURE V.25



