5.8.1: Potential Near a Point Mass

Last updated
Save as PDF

Page ID: 8145

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

We shall define the potential to be zero at infinity. If we are in the vicinity of a point mass, we shall always have to do work in moving a test particle away from the mass. We shan’t reach zero potential until we are an infinite distance away. It follows that the potential at any finite distance from a point mass is negative. The potential at a point is the work required to move unit mass from infinity to the point; i.e., it is negative.

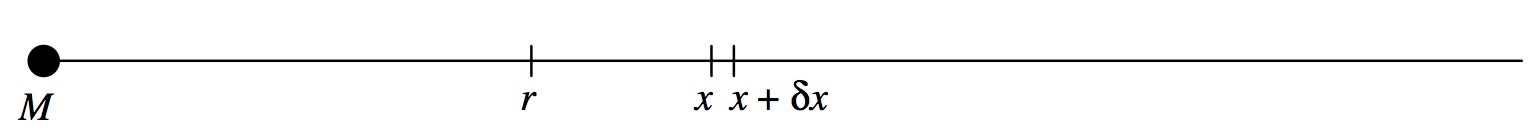
Figure 5.23.png
\(\text{FIGURE V.23}\)

The magnitude of the field at a distance \(x\) from a point mass \(M\) (figure \(\text{V.23}\)) is \(GM/x^2\), and the force on a mass m placed there would be \(GMm/x^2\). The work required to move \(m\) from \(x\) to \(x + δx\) is \(GMmδx/x^2\). The work required to move it from \(r\) to infinity is

\[GMm∫_r^∞ \frac{dx}{x^2} = \frac{GMm}{r}.\]

The work required to move unit mass from \(∞\) to \(r\), which is the potential at \(r\) is

\[ψ = -\frac{GM}{r}. \label{5.8.1} \tag{5.8.1}\]

The mutual potential energy of two point masses a distance r apart, which is the work required to bring them to a distance \(r\) from an infinite initial separation, is

\[V = -\frac{GMm}{r}. \label{5.8.2} \tag{5.8.2}\]

I here summarize a number of similar-looking formulas, although there is, of course, not the slightest possibility of confusing them. Here goes:

Force between two masses:

\[F = \frac{GMm}{r^2}. \quad \text{N} \label{5.8.3} \tag{5.8.3}\]

Field near a point mass:

\[g = \frac{GM}{r^2}, \quad \text{N kg}^{-1} \ or \text{ m s}^{-2} \label{5.8.4} \tag{5.8.4}\]

which can be written in vector form as:

\[\textbf{g} = - \frac{GM}{r^2} \hat{\textbf{r}} \quad \text{N kg}^{-1} \ or \text{ m s}^{-2} \label{5.8.5} \tag{5.8.5}\]

or as:

\[\textbf{g} = -\frac{GM}{r^3} \textbf{r}. \quad \text{N kg}^{-1} \ or \text{ m s}^{-2} \label{5.8.6} \tag{5.8.6}\]

Mutual potential energy of two masses:

\[V = -\frac{GMm}{r}. \quad \text{J} \label{5.8.7} \tag{5.8.7}\]

Potential near a point mass:

\[ψ = -\frac{GM}{r}. \quad \text{J kg}^{-1} \label{5.8.8} \tag{5.8.8}\]

I hope that’s crystal clear.