13.16: Topocentric-Geocentric Correction
( \newcommand{\kernel}{\mathrm{null}\,}\)
In section 13.1 I indicated two small (but not negligible) corrections that needed to be made, namely the ∆T correction (which can be made at the very start of the calculation) and the light-time correction, which can be made as soon as the geocentric distances have been determined – after which it is necessary to recalculate the geocentric distances from the beginning! I did not actually make these corrections in our numerical example, but I indicated how to do them.
There is another small correction that needs to be made. The diameter of Earth subtends an angle of 17".6 at 1 \ \text{au}, so the observed position of an asteroid depends appreciably on where it is observed from on Earth’s surface. Observations are, of course, reported as topocentric – i.e. from the place (τοπος) where the observer was situated. They must be corrected by the computer to geocentric positions – but of course that can’t be done until the distances are known. As soon as the distances are known, the light-time and the topocentric-geocentric corrections can be made. Then, of course, one has to return to the beginning and recompute the distances – possibly more than once until convergence is reached. This section shows how to make the topocentric-geocentric correction.
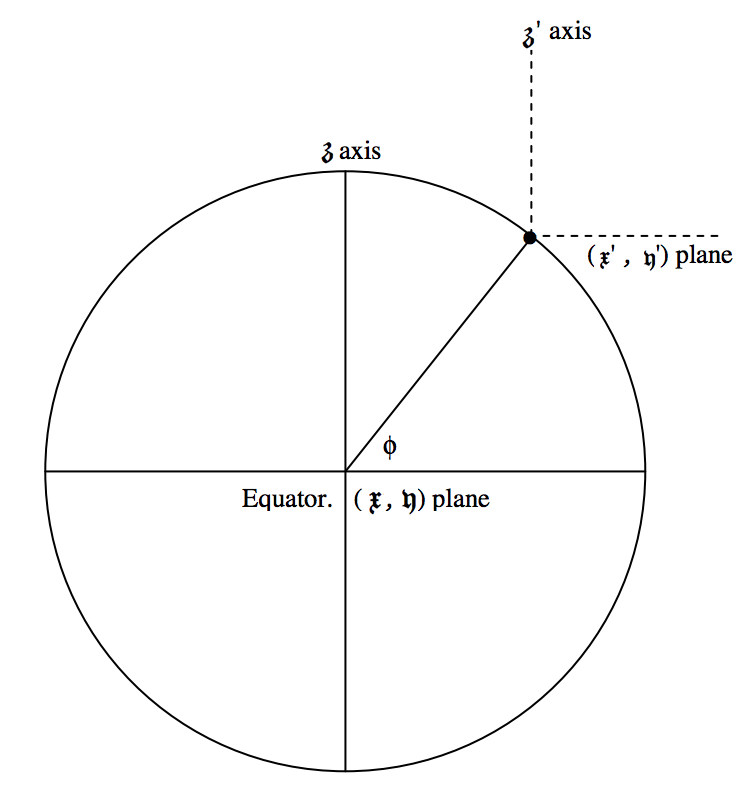
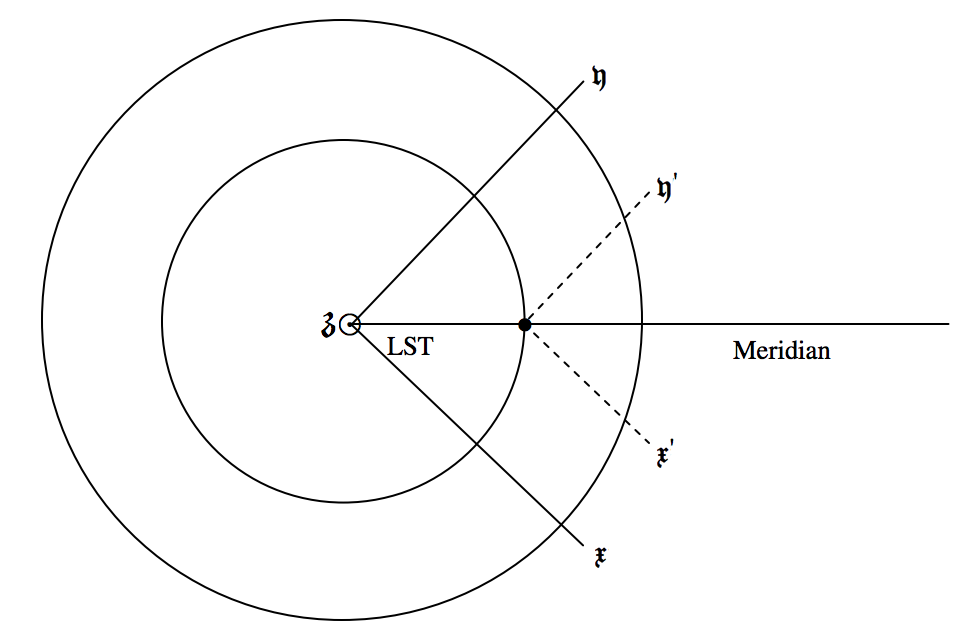
We have used the notation \mathfrak{x, y , z} for geocentric coordinates, and I shall use \mathfrak{x^\prime , \ y^\prime , \ z^\prime} for topocentric coordinates. In figure \text{XIII.3} I show Earth from a point in the equatorial plane, and from above the north pole. The radius of Earth is R, and the radius of a small circle of latitude \phi (where the observer is situated) is R \cos \phi. The \mathfrak{x}- and \mathfrak{x}^\prime - axes are directed towards the first point of Aries, \Upsilon.
It should be evident from the figure that the corrections are given by
\mathfrak{x}^\prime = \mathfrak{x} - R \cos \phi \cos \text{LST}, \label{13.16.1} \tag{13.16.1}
\mathfrak{y}^\prime = \mathfrak{y} - R \cos \phi \sin \text{LST} \label{13.16.2} \tag{13.16.2}
and \mathfrak{z}^\prime = \mathfrak{z} - R \sin \phi . \label{13.16.3} \tag{13.16.3}
Any observer who submits observations to the Minor Planet Center is assigned an Observatory Code, a three-digit number. This code not only identifies the observer, but, associated with the Observatory Code, the Minor Planet Center keeps a record of the quantities R \cos \phi and R \sin \phi in \text{AU}. These quantities, in the notation employed by the \text{MPC}, are referred to as −∆_{xy} and −∆_{z} respectively. They are unique to each observing site.
\text{FIGURE XIII.3}

