3.4: Velocity and Acceleration Components

Two-dimensional polar coordinates

Sometimes the symbols $r$ and $θ$ are used for two-dimensional polar coordinates, but in this section I use $(ρ , \phi)$ for consistency with the $(r, θ, \phi)$ of three-dimensional spherical coordinates. In what follows I am setting vectors in $\textbf{boldface}$. If you make a print-out, you should be aware that some printers apparently do not print Greek letter symbols in boldface, even though they appear in boldface on screen. You should be on the look-out for this. Symbols with ^ above them are intended as unit vectors, so you will know that they should be in boldface even if your printer does not recognize this. If in doubt, look at what appears on the screen.

$\text{FIGURE III.8}$

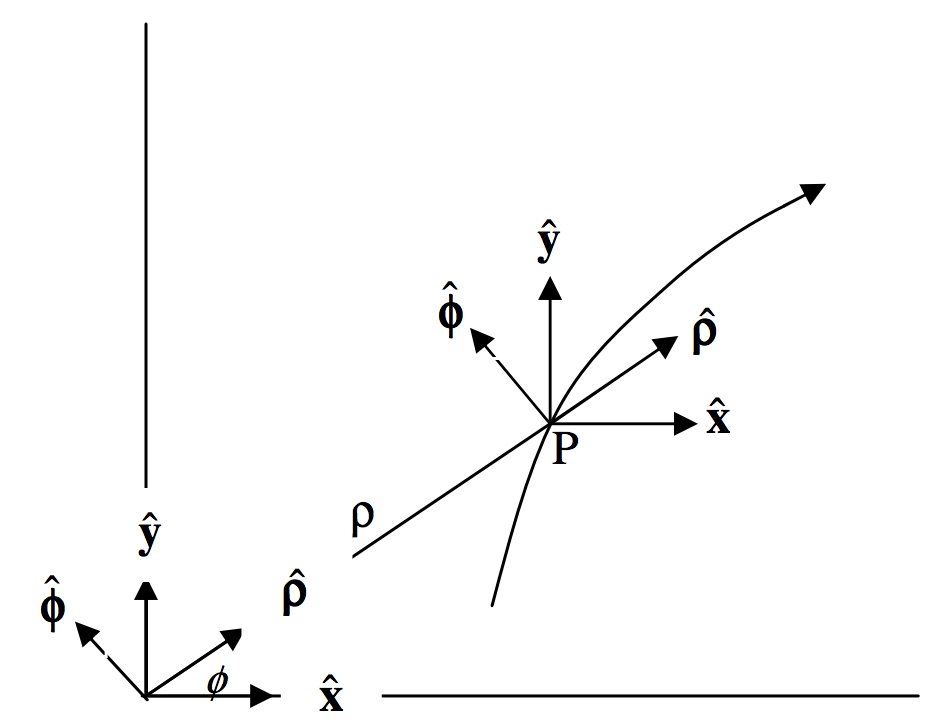
Figure $\text{III.8}$ shows a point $\text{P}$ moving along a curve such that its polar coordinates are changing at rates $\dot{ρ}$ and $\dot{\phi}$. The drawing also shows fixed unit vectors $\hat{x}$ and $\hat{y}$ parallel to the $x$- and $y$-axes, as well as unit vectors $\hat{\rho}$ and $\hat{\phi}$ in the radial and transverse directions. We shall find expressions for the rate at which the unit radial and transverse vectors are changing with time. (Being unit vectors, their magnitudes do not change, but their directions do.)

We have $$\boldsymbol{\hat{\rho}} = \cos \phi \boldsymbol{\hat{x}} + \sin \phi \boldsymbol{\hat{y}} \label{3.4.1} \tag{3.4.1}$$

and $$\boldsymbol{\hat{\phi}} = -\sin \phi \boldsymbol{\hat{x}} + \cos \phi \boldsymbol{\hat{y}}. \label{3.4.2} \tag{3.4.2}$$

$$\therefore \quad \boldsymbol{\dot{\hat{\rho}}} = - \sin \phi \dot{\phi} \boldsymbol{\hat{x}} + \cos \phi \dot{\phi} \boldsymbol{\hat{y}} = \dot{\phi} (-\sin \phi \boldsymbol{\hat{x}} + \cos \phi \boldsymbol{\hat{y}}) \label{3.4.3} \tag{3.4.3}$$

$$\therefore \quad \dot{\boldsymbol{\hat{\rho}}} = \dot{\phi} \boldsymbol{\hat{\phi}} \label{3.4.4} \tag{3.4.4}$$

In a similar manner, by differentiating Equation $\ref{3.4.2}$. with respect to time and then making use of Equation $\ref{3.4.1}$, we find

$$\boldsymbol{\dot{\hat{\phi}}} = - \dot{\phi} \boldsymbol{\hat{\rho}} \tag{3.4.5} \label{3.4.5}$$

Equations $\ref{3.4.4}$ and $\ref{3.4.5}$ give the rate of change of the radial and transverse unit vectors. It is worthwhile to think carefully about what these two Equations mean.

The position vector of the point $\text{P}$ can be represented by the expression $\boldsymbol{\rho} = \rho \boldsymbol{\hat{\rho}}$. The velocity of $\text{P}$ is found by differentiating this with respect to time:

$$\textbf{v} = \boldsymbol{\dot{\rho}} = \dot{\rho} \boldsymbol{\hat{\rho}} +\rho \boldsymbol{\dot{\hat{\rho}}} = \dot{\rho} \boldsymbol{\hat{\rho}} + \rho \dot{\phi} \boldsymbol{\hat{\phi}}. \label{3.4.6} \tag{3.4.6}$$

The radial and transverse components of velocity are therefore $\dot{\phi}$ and $\rho \dot{\phi}$ respectively. The acceleration is found by differentiation of Equation $\ref{3.4.6}$, and we have to differentiate the products of two and of three quantities that vary with time:

$$\begin{array}{c c c c l} \textbf{a} & = & \dot{\textbf{v}} & = & \ddot{\rho}\boldsymbol{\hat{\rho}} + \dot{\rho} \boldsymbol{\dot{\hat{\rho}}} + \dot{\rho} \dot{\phi} \boldsymbol{\hat{\phi}} + \rho \ddot{\phi} \boldsymbol{\hat{\phi}} + \rho \dot{\phi} \boldsymbol{\dot{\hat{\phi}}} \\ &&& = & \ddot{\rho} \boldsymbol{\hat{\rho}} + \dot{\rho} \dot{\phi} \boldsymbol{\hat{\phi}} + \dot{\rho} \dot{\phi} \boldsymbol{\hat{\phi}} + \rho \ddot{\phi} \boldsymbol{\hat{\phi}} - \rho \dot{\phi}^2 \boldsymbol{\hat{\rho}} \\ &&& = & \left( \ddot{\rho} - \rho \dot{\phi}^2 \right) \boldsymbol{\hat{\rho}} + \left( \rho \ddot{\phi} + 2 \dot{\rho} \dot{\phi} \right) \boldsymbol{\hat{\phi}} . \\ \tag{3.4.7} \label{3.4.7} \end{array}$$

The radial and transverse components of acceleration are therefore $(\ddot{\rho} − \rho \dot{\phi}^2)$ and $(\rho \ddot{\phi} + 2 \dot{\rho} \dot{\phi})$ respectively.

Three-Dimensional Spherical Coordinates

In figure $\text{III.9}$, $\text{P}$ is a point moving along a curve such that its spherical coordinates are changing at rates $\dot{r}, \dot{θ}, \dot{\phi}$. We want to find out how fast the unit vectors $\hat{\textbf{r}}$, $\boldsymbol{\hat{\theta}}$, $\boldsymbol{\hat{\phi}}$ in the radial, meridional and azimuthal directions are changing.

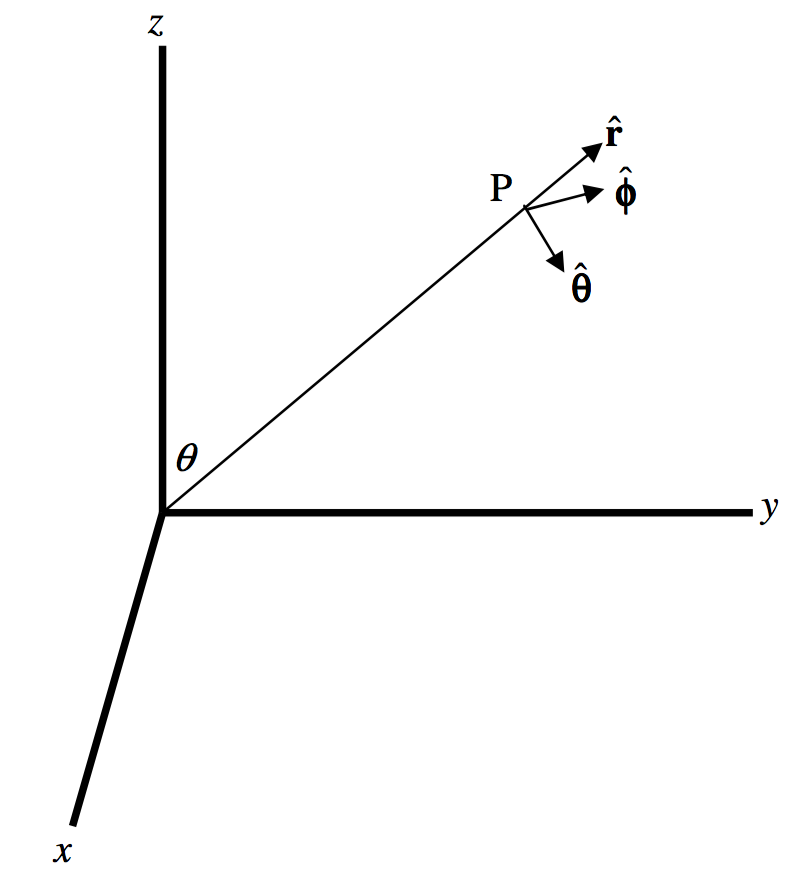
$\text{FIGURE III.9}$

We have $$\hat{\textbf{r}} = \sin θ \cos \phi \hat{\textbf{x}} + \sin θ \sin \phi \hat{\textbf{y}} + \cos θ \hat{\textbf{z}} \label{3.4.8} \tag{3.4.8}$$

$$\boldsymbol{\hat{\theta}} = \cos θ \cos \phi \hat{\textbf{x}} + \cos θ \sin \phi \hat{\textbf{y}} - \sin θ \hat{\textbf{z}} \label{3.4.9} \tag{3.4.9}$$

$$\boldsymbol{\hat{\phi}} = - \sin \phi \hat{\textbf{x}} + \cos \phi \hat{\textbf{y}} \label{3.4.10} \tag{3.4.10}$$

$$\therefore \quad \dot{\hat{\textbf{r}}} = (\cos θ \dot{θ} \cos \phi - \sin θ \sin \phi \dot{\phi} ) \hat{\textbf{x}} + (\cos θ \dot{θ} \sin \phi + \sin θ \cos \phi \dot{\phi} ) \hat{\textbf{y}} - \sin θ \dot{θ} \hat{\textbf{z}}. \label{3.4.11} \tag{3.4.11}$$

We see, by comparing this with Equations $\ref{3.4.9}$ and $\ref{3.4.10}$ that

$$\dot{\hat{\textbf{r}}} = \dot{θ} \boldsymbol{\hat{\theta}} + \sin θ \dot{\phi} \boldsymbol{\hat{\phi}} \label{3.4.12} \tag{3.4.12}$$

By similar arguments we find that

$$\boldsymbol{\dot{\hat{\theta}}} = \cos θ \dot{\phi} \boldsymbol{\hat{\phi}} - \dot{θ} \hat{\textbf{r}} \label{3.4.13} \tag{3.4.13}$$

and

$$\boldsymbol{\dot{\hat{\phi}}} = - \sin θ \dot{\phi} \hat{\textbf{r}} - \cos θ \dot{\phi} \boldsymbol{\hat{\theta}} \label{3.4.14} \tag{3.4.14}$$

These are the rates of change of the unit radial, meridional and azimuthal vectors. The position vector of the point $\text{P}$ can be represented by the expression $\textbf{r} = r \ \hat{\textbf{r}}$. The velocity of $\text{P}$ is found by differentiating this with respect to time:

$$\begin{array}{c c c} \textbf{v} & = & \dot{\textbf{r}} = \dot{r} \hat{\textbf{r}} + r \ \dot{\hat{\textbf{r}}} = \dot{r} \hat{r} + r(\dot{θ} \boldsymbol{\hat{\theta}} + \sin θ \dot{\phi} \boldsymbol{\hat{\phi}} ) \\ & = & \dot{r} \hat{\textbf{r}} + r \ \dot{θ} \boldsymbol{\hat{\theta}} + r \sin θ \dot{\phi} \boldsymbol{\hat{\phi}} \\ \label{3.4.15} \tag{3.4.15} \end{array}$$

The radial, meridional and azimuthal components of velocity are therefore $\dot{r}, \ r \dot{θ}$ and $r \sin θ \dot{\phi}$ respectively.

The acceleration is found by differentiation of Equation $\ref{3.4.15}$.

It might not be out of place here for a quick hint about differentiation. Most readers will know how to differentiate a product of two functions. If you want to differentiate a product of several functions, for example four functions, $a, \ b, \ c$ and $d$, the procedure is

$$(abcd)^\prime = a^\prime bcd + ab^\prime cd + abc^\prime d + abcd^\prime. \nonumber$$

In the last term of Equation $\ref{3.4.15}$, all four quantities vary with time, and we are about to differentiate the product.

$$\textbf{a} = \dot{\textbf{v}} = \ddot{r} \hat{\textbf{r}} + \dot{r} ( \dot{θ} \boldsymbol{\hat{\theta}} + \sin θ \dot{\phi} \boldsymbol{\hat{\phi}}) + \dot{r} \dot{θ} \boldsymbol{\hat{\theta}} + r \ddot{\theta} \boldsymbol{\hat{\theta}} + r \dot{θ} ( \cos θ \dot{\phi} \boldsymbol{\hat{\phi}} - \dot{θ} \hat{\textbf{r}} ) + \dot{r} \sin θ \dot{\phi} \boldsymbol{\hat{\phi}} + r \cos θ \dot{θ} \dot{\phi} \boldsymbol{\hat{\phi}} + r \sin θ \ddot{\phi} \boldsymbol{\hat{\phi}} + r \sin θ \dot{\phi} ( - \sin θ \dot{\phi} \hat{\textbf{r}} - \cos θ \dot{\phi} \boldsymbol{\hat{\theta}}) \tag{3.4.16} \label{3.4.16}$$

On gathering together the coefficients of $\hat{\textbf{r}}, \boldsymbol{\hat{\theta}}, \boldsymbol{\hat{\phi}}$, we find that the components of acceleration are:

• Radial: $\ddot{r} - r \dot{θ}^2 - r \sin^2 θ \dot{\phi}^2$
• Meridional: $r \ddot{θ} + 2\dot{r} \dot{θ} - r \sin θ \cos θ \dot{\phi}^2$
• Azimuthal: $2 \dot{r} \dot{\phi} \sin θ + 2r \dot{θ} \dot{\phi} \cos θ + r \sin θ \ddot{\phi}$