8.4: Direct and Retrograde Motion, and Stationary Points
- Page ID
- 6836
As seen from the north ecliptic pole, the major planets move counterclockwise around the Sun. Such motion is called direct or prograde motion. A body moving clockwise (such as some comets) is said to be moving retrograde.
In figure \(\text{VIII.4}\) I have drawn Earth moving around the Sun at angular speed \(ω_0\) and a superior planet (which I have indicated at opposition and at conjunction) moving with slower angular speed \(ω\).
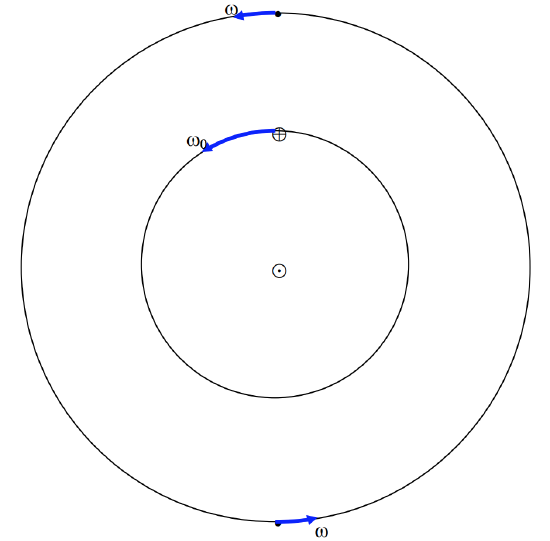
\(\text{FIGURE VIII.4}\)
In figure \(\text{VIII.5}\). I have drawn the same situation but referred to what I call a synodic reference frame. That is, a reference frame that is co-rotating with Earth, such that the Earth-Sun line is stationary. In the synodic frame, the planet is moving clockwise at angular speed \(ω − ω_0\).
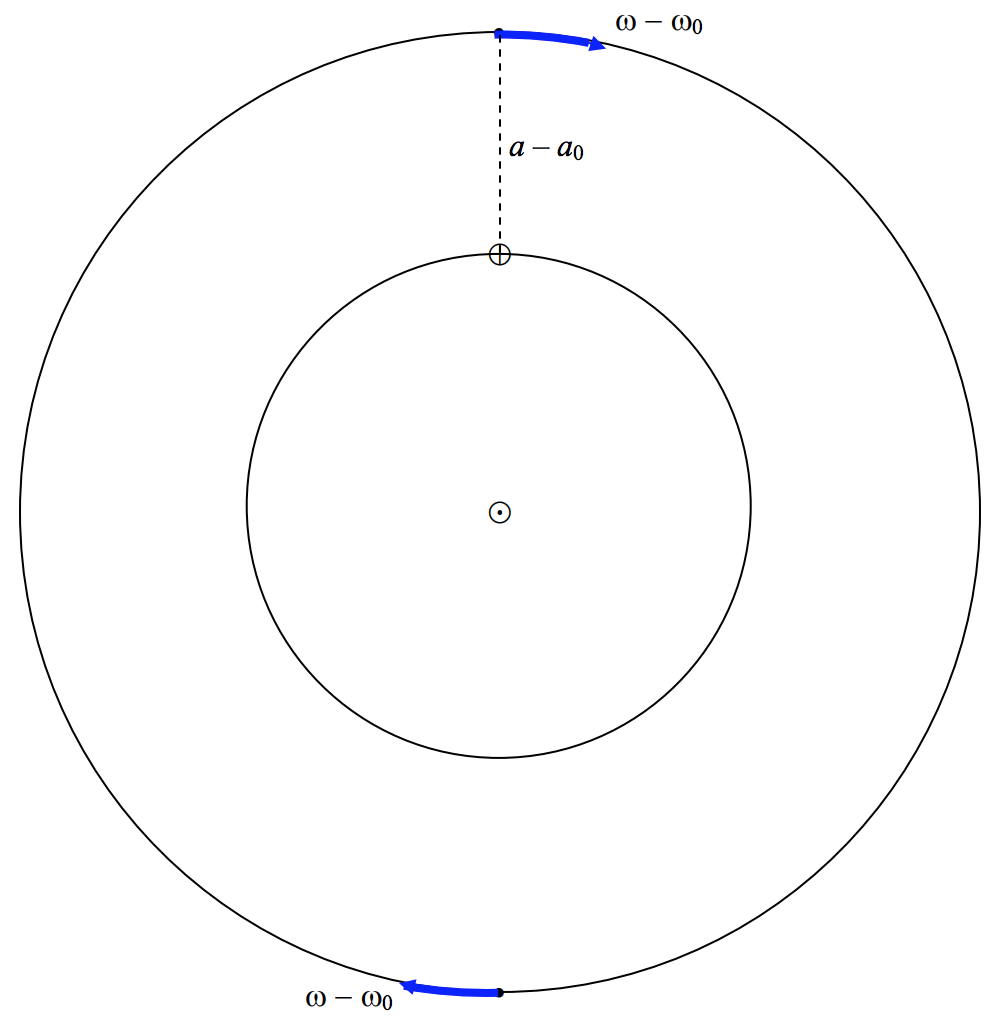
\(\text{FIGURE VIII.5}\)
Let \(a_0\) and \(a\) be the radii or Earth’s and the planet’s orbit respectively. In that case, the angular speed of the planet in the sidereal frame is, by Kepler’s third law, \(ω = ω_0 \left( \frac{a_0}{a} \right)^{3/2}\) counterclockwise, and therefore, in the synodic frame, it is \(ω_0 \left[ 1 - \left( \frac{a_0}{a} \right)^{3/2} \right]\) clockwise. From this point, I am going to express angular speeds in units of \(ω_0\) and distances in astronomical units (\(a_0 = 1\)). In these units, then, the angular speed of the planet around the Sun in the synodic frame is \(1 – a^{−3/2}\) clockwise, and its linear speed in its orbit (of radius \(a\)) is \(a(1 – a^{−3/2})\).
Now suppose the planet is at opposition, so that its distance from Earth is \(a – 1\). The angular speed of the planet as seen from Earth is therefore \(\frac{a ( - a^{-3/2})}{a-1}\) clockwise. For superior planets and asteroids (\(a > 1\)), this goes from \(1.5\) to \(1.0\) as \(a\) goes from \(1\) to \(∞\). Now in the synodic frame, the celestial sphere with the fixed stars upon it is revolving around Earth at angular speed \(1\). Therefore, at opposition, the angular speed of the planet against the background of stars (also known as the apparent proper motion, for which I shall use the symbol \(p\)) of the planet is the above expression minus \(1\), which, after simplification, becomes
\[p = \frac{1 - 1/\sqrt{a}}{a-1} \label{8.4.1} \tag{8.4.1}\]
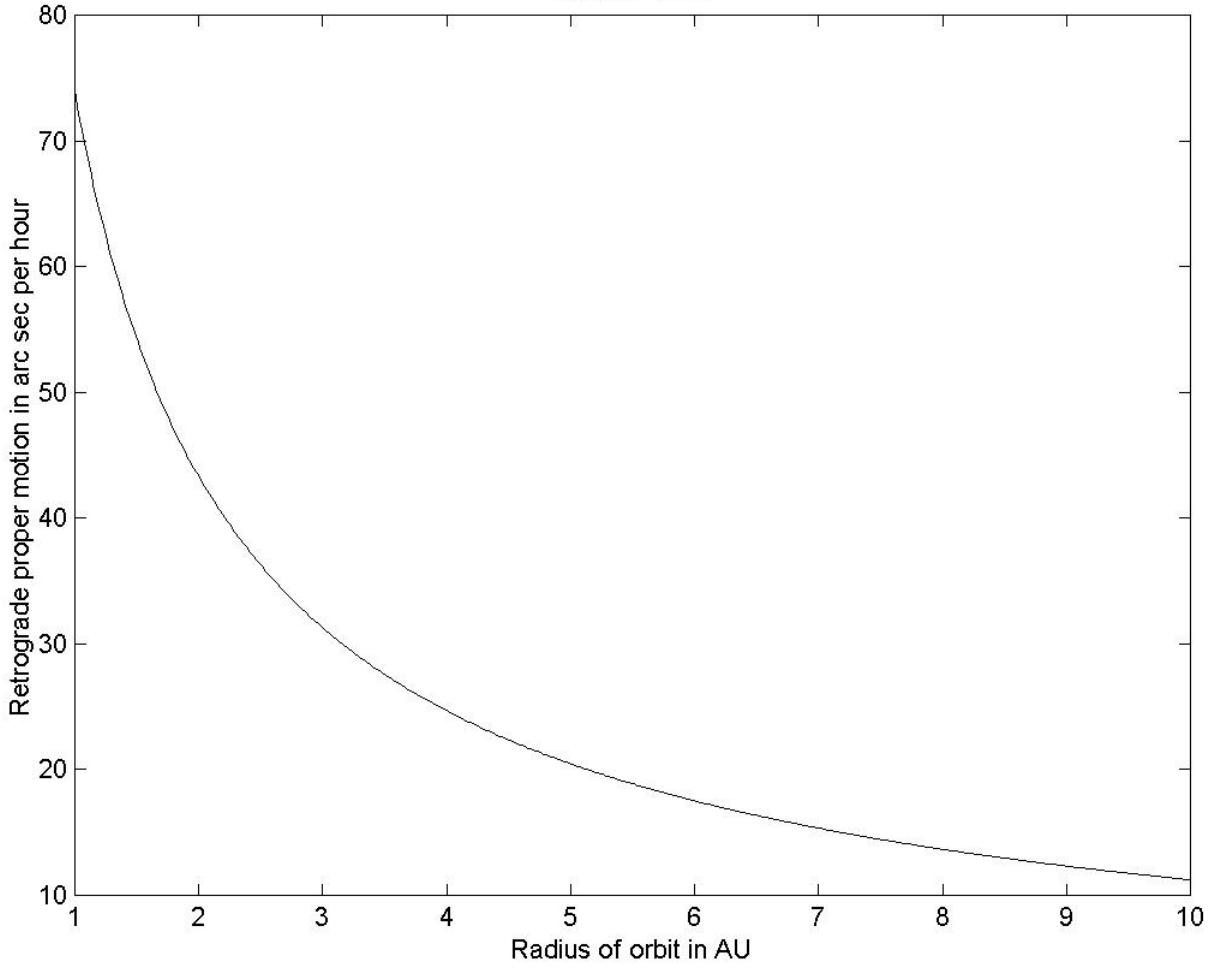
in the direction of decreasing ecliptic longitude or decreasing right ascension – i.e. towards the west. That is to say, at opposition, the planet appears from Earth to be moving in the retrograde direction. The reader is reminded that, in Equation \ref{8.4.1}, \(p\) is the proper motion to the west, in units of \(ω_0 = 147.8\) arcseconds per mean solar hour, and \(a\) is the radius of the planet’s orbit in \(\text{AU}\). A graph of \(p\) versus \(a\) is shown in figure \(\text{VIII.6}\).
Equation \ref{8.4.1} enables us to calculate \(p\) given \(a\). The more interesting problem is to calculate \(a\) given \(p\). Thus, you are searching for asteroids near the opposition point one night, and a new planet swims into your ken. (That’s from a poem by Keats, by the way.) You see that it is moving retrograde with respect to the stars by so many arcseconds per hour. Assuming that it is moving in a circular orbit, what is the radius of its orbit? The quick answer, of course, is to look at figure \(\text{VIII.6}\), but you can also keep your hand at high-school algebra in by inverting Equation \ref{8.4.1} to obtain
\[a = \frac{p+2 - \sqrt{p(p+4)}}{2p}. \label{8.4.2} \tag{8.4.2}\]
Similar considerations for an inferior planet will show that, at inferior conjunction, the angular speed of the planet towards the west is \(\frac{a(a^{-3/2} - 1)}{1-a}\), which is the same as the formula for a superior planet at opposition. As \(a\) goes from \(1\) to \(0\), this goes from \(1.5\) to \(∞\). In the synodic frame, the stars are moving westward at angular speed \(1\), so, relative to the background stars, an inferior planet at inferior conjunction has a retrograde (westward) proper motion given by the same formula as for a superior planet at superior conjunction, namely Equation \ref{8.4.1}. A graph of \(p\) versus \(a\) for an inferior planet drops from \(∞\) at \(a = 0\) to \(73.9\) arcsec per hour at \(a = 1\). Just to keep your algebra skills polished, you can show from Equation \ref{8.4.1} that when \(a = 1\), \(p = ½\).
\(\text{FIGURE VIII.6}\)
Thus a superior planet at opposition moves westward (it “retrogrades”) relative to the stars, and an inferior planet at inferior conjunction also moves westward (it “retrogrades”) relative to the stars.
It will, however, be obvious that a superior planet at conjunction, or an inferior planet at superior conjunction, will move eastward (“direct” or “prograde”) relative to the stars. Therefore at some point in its orbit a planet will be stationary relative to the stars at the moment when its proper motion changes from direct to retrograde. As seen from Earth, a planet moves generally eastward relative to the stars, except for a short time near opposition (for a superior planet) or inferior conjunction (for an inferior planet) when it briefly retrogrades towards the west. It is small wonder that the ancient astronomers, believing that the Earth was at the centre of the solar system, believed in their system of deferents and epicycles. We would believe the same today if we hadn’t read differently in books and on this web site.
Two small words of caution. It is sometimes believed by the unwary that the stationary points in the orbit of an inferior planet occur when the planet is at greatest elongation from the Sun. This is not the case, and indeed there is a small exercise on this point in the penultimate paragraph of this chapter. The second small point to notice is that, for precise work, it is necessary to distinguish between when a planet is stationary (i.e. it is at the moment of changing direction) in right ascension, and when it is stationary in ecliptic longitude. In our simple model of coplanar orbits, we need not make this fine distinction.
In what follows, we are going to calculate (for our concentric circular coplanar model) the angular distance of a superior planet from the opposition point when it is stationary, and the angular distance (“elongation”) from the Sun when an inferior planet is stationary. We’ll start with a superior planet.
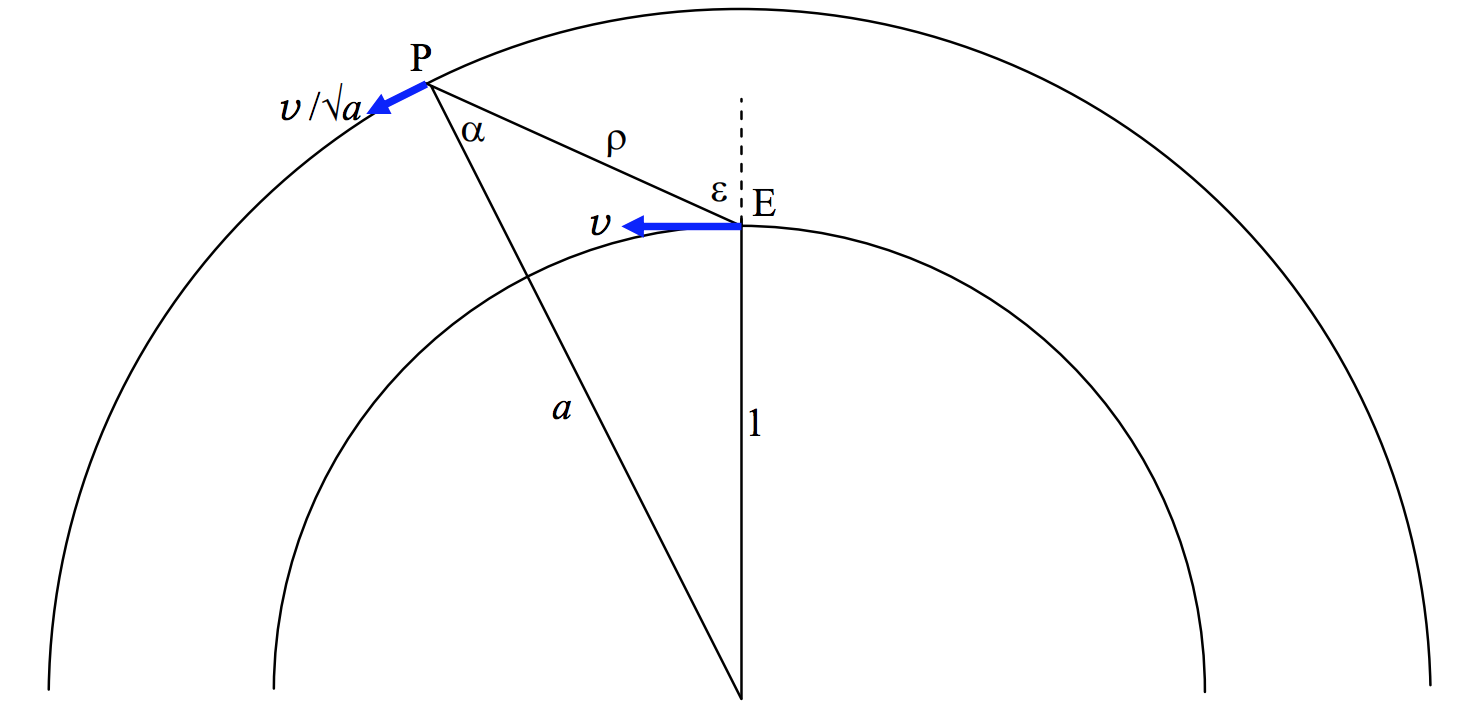
\(\text{FIGURE VIII.7}\)
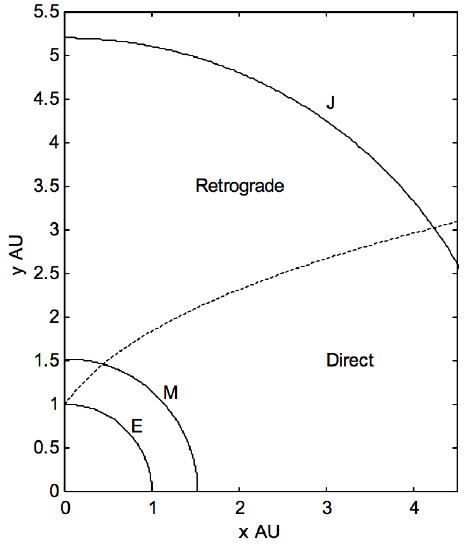
Figure \(\text{VIII.7}\) shows the Earth \(\text{E}\) moving in its orbit of radius \(1 \ \text{AU}\) with speed \(v\), and a superior planet or asteroid \(\text{P}\) moving in its orbit of radius \(a \ \text{AU}\) with speed \(v /√a\). The angle \(ε\) is the angular distance of the planet from the opposition point. The angle \(α\) is known as the phase angle. There is no apparent motion of the planet against the starry background (i.e. the planet is at its stationary point) when the components of the two velocity vectors perpendicular to the line \(\text{EP}\) are equal. That is, the planet is at a stationary point when \( \frac{v}{\sqrt{a}} \cosα = v \cos ε\), or
\[\cos α = \sqrt{a} \cos ε. \label{8.4.3} \tag{8.4.3}\]
But from triangle \(\text{SEP}\) we have
\[a \sin α = \sin ε . \label{8.4.4} \tag{8.4.4}\]
On elimination of \(α\) from Equations \ref{8.4.3} and \ref{8.4.4}, we find that the planet is at a stationary point when its angular distance from the opposition point is given by
\[\tan ε = \frac{a}{\sqrt{1+a}}. \label{8.4.5} \tag{8.4.5}\]
On inversion of this Equation (do it!), we find that the heliocentric distance of a planet which reaches it stationary point at an angular distance \(ε\) from the opposition point is
\[a = \frac{1}{2} \left( t + \sqrt{t(t+4)} \right) , \label{8.4.6} \tag{8.4.6}\]
where \(t = \tan^2 ε\).
The relation between \(a\) and \(ε\) is shown in figure \(\text{VIII.8}\). The least possible angular distance of the stationary point from opposition for a superior planet moving in a circular orbit is \(\tan^{−1} 1/(√2) = 35^\circ \ 16^\prime = 02^\text{h} \ 21^\text{m}\).
\(\text{FIGURE VIII.8}\)
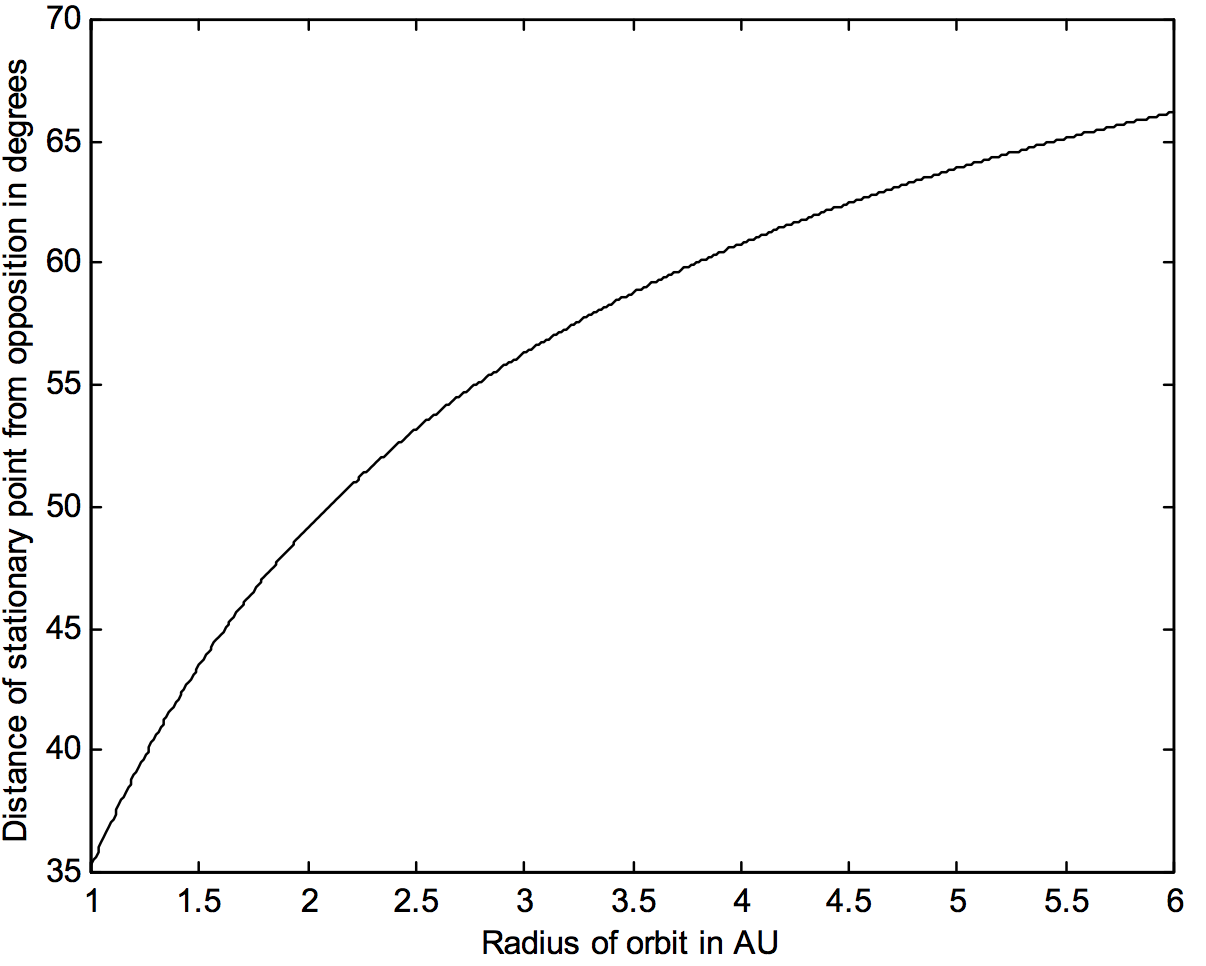
Figure \(\text{VIII.9}\), in which the Sun is at the origin, shows the orbits of Earth, Mars and Jupiter, and it divides the area in which asteroids moving in circular orbits will have direct or retrograde proper motions.
\(\text{FIGURE VIII.9}\)
If the reader carries out the same analysis for inferior planets, he or she will find that Equations \(\ref{8.4.4}\) to \(\ref{8.4.6}\) apply equally well, except that, in the case of inferior planets (and inferior asteroids, such as the Aten group, of which more are likely to be discovered in the coming years) the angle \(ε\) is the angular distance or elongation of the planet from the Sun rather than from the opposition point, and \(35^\circ 16^\prime\) is the greatest value this may have for the stationary point of an inferior planet in a circular orbit. The Equation corresponding to \(\ref{8.4.3}\) becomes, for in inferior planet, \(\cos α = − \sqrt{a} \cos ε\). The elongation of the stationary point is, unsurprisingly, less than the greatest elongation. Also, for an inferior planet, it is to be noted that, for a given elongation (other than greatest elongation) two phase angles are possible and two geocentric distances are possible. At the stationary point, the obtuse phase angle and the lesser of the two geocentric distances are the correct ones.
Of course in general, we are not likely to be observing an asteroid exactly at the opposition point or exactly at a stationary point. We now tackle the slightly more difficult problem: What is the proper motion of an asteroid whose circular orbital radius is \(a\) when it is observed at an angular distance \(ε\) from the opposition point (or from the Sun)? Or, conversely, if we observe an asteroid at an angular distance \(ε\) from the opposition point, and we see that it has a proper motion \(p\), what is the radius of its (assumed circular) orbit?
In figure 9b we see, in a sidereal reference frame, the orbits of Earth, \(\text{E}\), and a superior planet (or asteroid), \(\text{P}\), the radii of their orbits being \(1\) and \(a \ \text{AU}\). The heliocentric and geocentric distances of the planet are \(a\) and \(ρ\). The angular distance of the planet from the opposition point is \(ε\) and the phase angle is \(α\). Earth is moving with angular speed 1 (in units of \(ω_0\)) and the planet is moving (according to Kepler’s third law) with angular speed \(a^{−3/2}\).
In figure 9c we see the same situation in a synodic reference frame, in which Earth is stationary and the planet is moving clockwise at an angular speed \(1 − a^{−3/2}\) (in units of \(ω_0\)).
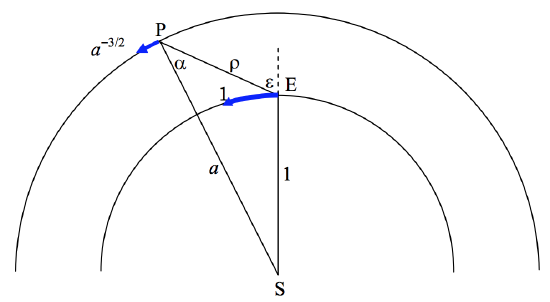
\(\text{FIGURE VIII.9B}\)
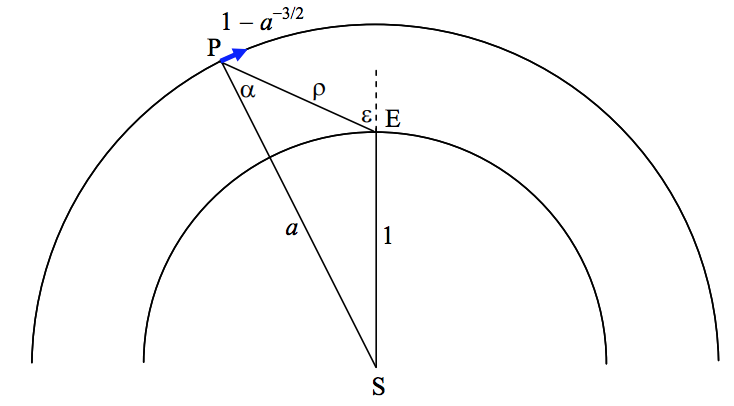
\(\text{FIGURE VIII.9C}\)
In the synodic frame, the linear speed of the planet (whose angular speed is \(1 − a^{−3/2}\) and whose heliocentric distance is \(a\)) is
\[a(1 - a^{-3/2} ) = a - \frac{1}{\sqrt{a}}. \label{8.4.7} \tag{8.4.7}\]
The transverse component of this velocity as seen from Earth is
\[\left( a - \frac{1}{\sqrt{a}} \right) \cos α, \label{8.4.8} \tag{8.4.8}\]
so that its angular velocity as seen from Earth is
\[\frac{1}{ρ} \left( a - \frac{1}{\sqrt{a}} \right) \cos α \label{8.4.9} \tag{8.4.9}\]
retrograde.
In the synodic frame, the stars are moving retrograde at angular speed \(1\). Therefore the planet is moving direct relative to the background stars at angular speed
\[p = 1 - \frac{1}{ρ} \left( a - \frac{1}{\sqrt{a}} \right) \cos α \label{8.4.10} \tag{8.4.10}\]
and this is the required proper motion. In this Equation, geometry shows that
\[a \sin α = \sin ε \label{8.4.11} \tag{8.4.11}\]
and \[ρ^2 = 1 + a[a - 2 \cos (ε - α) ] . \label{8.4.12} \tag{8.4.12}\]
Thus \(p\) can be calculated, given \(ε\) and \(a\).
The more interesting and practical problem, however, is that you have observed an asteroid at an angular distance \(ε\) from the opposition point, and it is moving at an angular speed \(p\) relative to the starry background. (We’ll count \(p\) as positive if the proper motion is direct – i.e. if the asteroid is moving eastward relative to the stars. The sign of \(ε\) does not matter.) You are going to have to invert Equation \ref{8.4.10}. I am not sure if this can easily be done algebraically, so your challenge is to write a computer program that will return a numerically given \(p\) and \(ε\) as input data. It can be done, but I shall not pretend that it is easy.
When you have done this, here are three examples for you:
1. Proper motion = 40 arcsec per hour westward; i.e. \(p = −40\) arcsec per hour. \(ε = 20^\circ\). Find the heliocentric distance \(a\) in \(\text{AU}\).
2. \(p = +40"/\text{hr}. \ ε = 70^\circ\). Find \(a\).
3. \(p = −15"/\text{hr}. \ ε = 40^\circ\). Find \(a\).
I have written my own Fortran program to invert Equation \(\ref{8.4.10}\), using Newton-Raphson iteration, and here are the answers it gives me.
1. \(a = 1.578 \ \text{AU}\)
2. \(a = 1.718 \ \text{AU}\)
3. Error message!
My computer failed to do example number 3! In other words, given a proper motion of \(−15"/\text{hr}\) and an opposition distance of \(40^\circ\), it could not tell me the heliocentric distance!
In figure \(\text{VIII.10}\) I have plotted proper motion versus \(ε\) for several heliocentric distances, and in figure \(\text{VIII.11}\) I have drawn proper motion versus heliocentric distance for several \(ε\). You will find that you can easily find approximate solutions to the first two of these problems from either figure, but you cannot solve the third problem from either figure. In other words, given certain combinations of \(p\) and \(ε\), it simply is not possible to determine \(a\). There is a large range of value of \(a\) and \(ε\) that result in the same proper motion.
If you carry out the same analysis for inferior planets, you will find that the Equations that correspond to Equations 8,4,10-12 are as follows:
\[p = 1 + \frac{1}{ρ} \left( \frac{1}{\sqrt{a}} - a \right) \cos α . \label{8.4.13} \tag{8.4.13}\]
This is the same as Equation \ref{8.4.10}.
\[a \sin α = \sin ε . \label{8.4.14} \tag{8.4.14}\]
This is the same as Equation \ref{8.4.11}, except that, for an inferior planet, \(ε\) is the elongation from the Sun and there are two solutions for \(α\), one acute and the other obtuse. As Galileo announced: Cynthiae figuras aemulatur mater amorum.
The Equation that corresponds to Equation \ref{8.4.12} is
\[ρ^2 = 1 + a [ a + 2 \cos (ε + α) ] , \label{8.4.15} \tag{8.4.15}\]
which differs slightly from Equation \ref{8.4.12}
\(\text{FIGURE VIII.10}\)
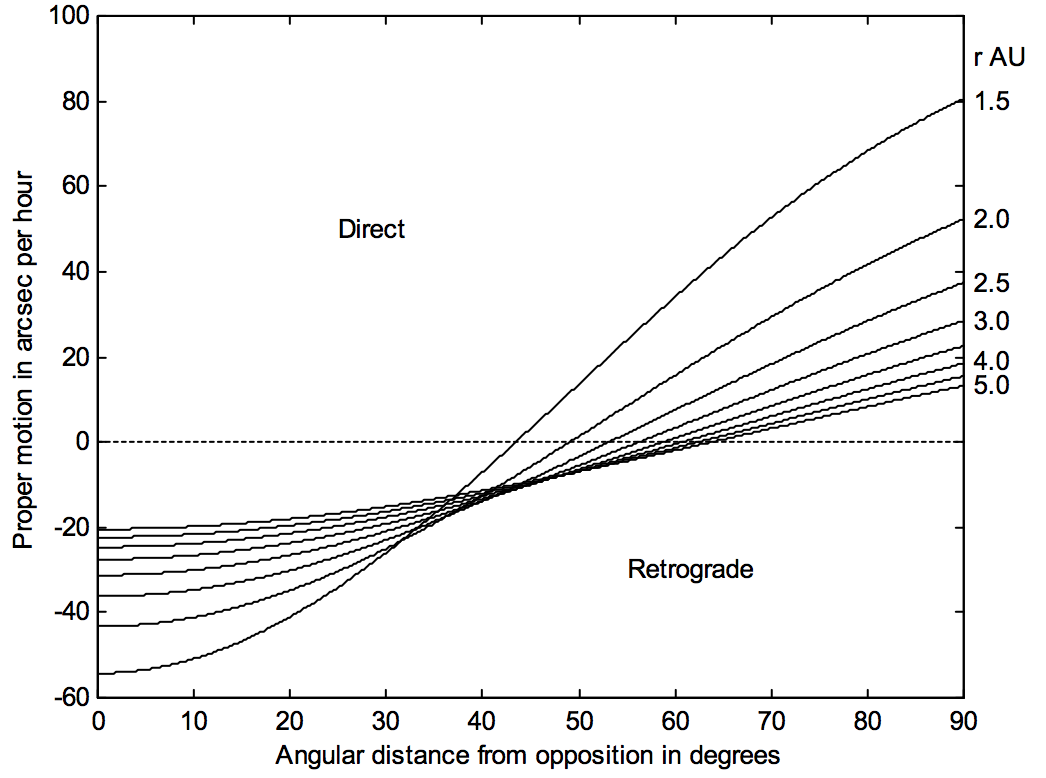
\(\text{FIGURE VIII.11}\)
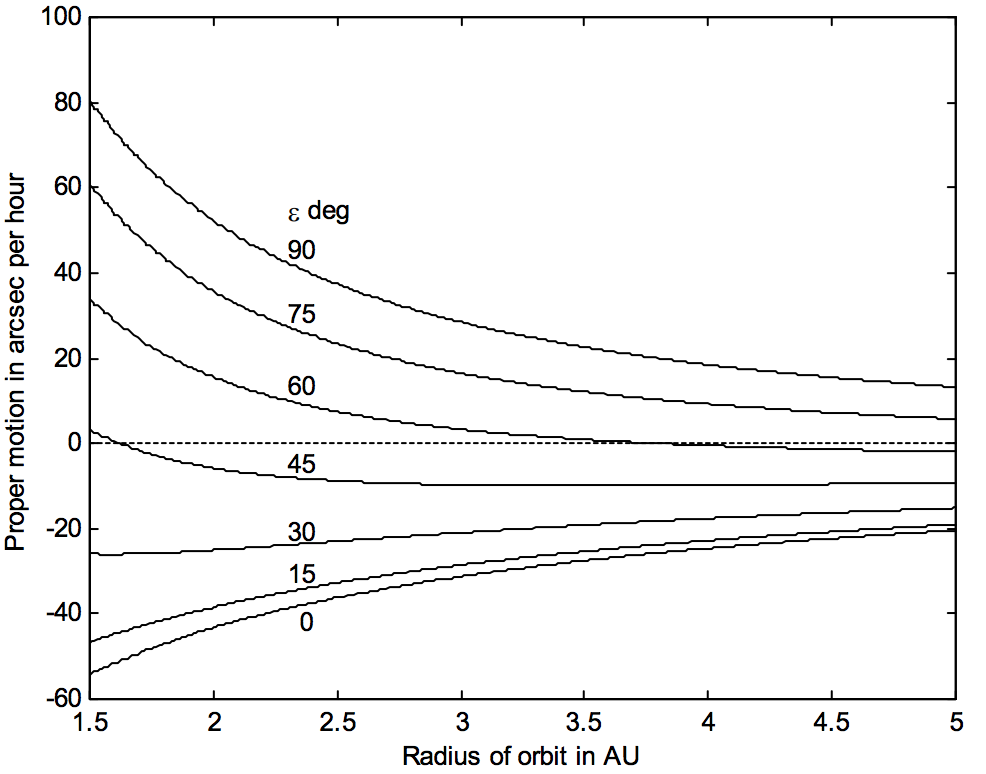
In figure \(\text{VIII.12}\) I have plotted the proper motion versus elongation from the Sun for several inferior heliocentric distances. You will observe that, for a given elongation and proper motion, there are two possible solutions for \(a\), and there is nothing you can do about it from a single observation of \(ε\) and \(p\). For \(ε = 0\) (conjunction with the Sun), the proper motion is positive at superior conjunction and negative at inferior conjunction.
\(\text{FIGURE VIII.12}\)
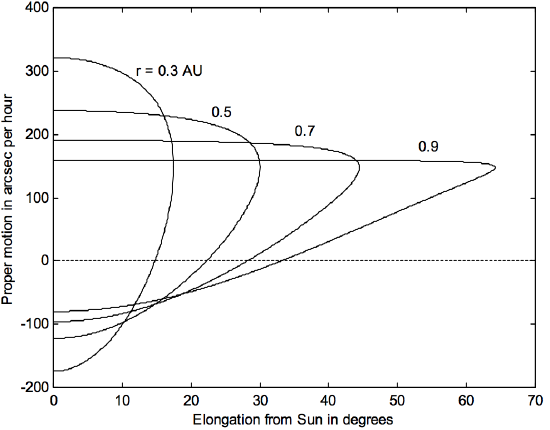
As an exercise, you might like to convince yourself – either from the Equations or just from the geometry of the situation − that the proper motion relative to the stars of any inferior planet in a circular orbit at greatest elongation is independent of the radius of the orbit. What is this proper motion in arcsec per hour?
Summary. The graphs and Equations in this section will enable an estimate to be made of the radius of the orbit of an asteroid to be estimated from a single night’s observation of its proper motion and angular distance from the opposition point (superior asteroid) or from the Sun (inferior asteroid). The assumptions made are that Earth and asteroid are in coplanar circular orbits. While this is not the case for many asteroids, it is a reasonable approximation for most of the asteroids at least in the main belt. However, there are some combinations of \(p\) and \(ε\) for which a solution cannot be obtained, and, for inferior asteroids, there are always two possible solutions.


