15.4: One-Dimensional Collisions Between Two Objects

One Dimensional Elastic Collision in Laboratory Reference Frame

Consider a one-dimensional elastic collision between two objects moving in the x - direction. One object, with mass $m_{1}$ and initial x -component of the velocity $\mathcal{V}_{1 x, i}$ collides with an object of mass $m_{2}$ and initial x -component of the velocity $\mathcal{V}_{2 x, i}$. The scalar components $v_{1 x, i}$ and $v_{1 x, i}$ can be positive, negative or zero. No forces other than the interaction force between the objects act during the collision. After the collision, the final x -component of the velocities are $v_{1 x, f}$ and $v_{2 x, f}$. We call this reference frame the “laboratory reference frame”.

Figure 15.5 One-dimensional elastic collision, laboratory reference frame

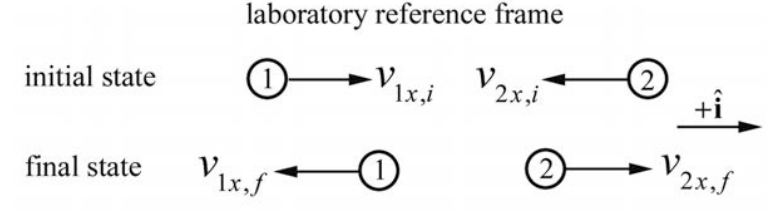
For the collision depicted in Figure 15.5, $v_{1 x, i}>0, \quad v_{2 x, i}<0, \quad v_{1 x, f}<0$, and $v_{2 x, f}>0$. Because there are no external forces in the x -direction, momentum is constant in the x - direction. Equating the momentum components before and after the collision gives the relation

$$m_{1} v_{1 x, i}+m_{2} v_{2 x, i}=m_{1} v_{1 x, f}+m_{2} v_{2 x, f} \nonumber$$

Because the collision is elastic, kinetic energy is constant. Equating the kinetic energy before and after the collision gives the relation

$$\frac{1}{2} m_{1} v_{1 x, i}^{2}+\frac{1}{2} m_{2} v_{2 x, i}^{2}=\frac{1}{2} m_{1} v_{1 x, f}^{2}+\frac{1}{2} m_{2} v_{2 x, f}^{2} \nonumber$$

Rewrite these Equations (15.3.1) and (15.3.2) as

$$m_{1}\left(v_{1 x, i}-v_{1 x, f}\right)=m_{2}\left(v_{2 x, f}-v_{2 x, i}\right) \nonumber$$

$$m_{1}\left(v_{1 x, i}^{2}-v_{1 x, f}^{2}\right)=m_{2}\left(v_{2 x, f}^{2}-v_{2 x, i}^{2}\right) \nonumber$$

Equation (15.3.4) can be written as

$$m_{1}\left(v_{1 x, i}-v_{1 x, f}\right)\left(v_{1 x, i}+v_{1 x, f}\right)=m_{2}\left(v_{2 x, f}-v_{2 x, i}\right)\left(v_{2 x, f}+v_{2 x, i}\right) \nonumber$$

Divide Equation (15.3.4) by Equation (15.3.3), yielding

$$v_{1 x, i}+v_{1 x, f}=v_{2 x, i}+v_{2 x, f} \nonumber$$

Equation (15.3.6) may be rewritten as

$$v_{1 x, i}-v_{2 x, i}=v_{2 x, f}-v_{1 x, f} \nonumber$$

Recall that the relative velocity between the two objects is defined to be

$$\overrightarrow{\mathbf{v}}^{\mathrm{rel}} \equiv \overrightarrow{\mathbf{v}}_{1,2} \equiv \overrightarrow{\mathbf{v}}_{1}-\overrightarrow{\mathbf{v}}_{2} \nonumber$$

where we used the superscript “rel” to remind ourselves that the velocity is a relative velocity (and to simplify our notation). Thus $v_{x, i}^{\mathrm{rel}}=v_{1 x, i}-v_{2 x, i}$ is the initial x -component of the relative velocity, and $v_{x, f}^{\mathrm{rel}}=v_{1 x, f}-v_{2 x, f}$ is the final x -component of the relative velocity. Therefore Equation (15.3.7) states that during the interaction the initial relative velocity is equal to the negative of the final relative velocity.

$\overrightarrow{\mathbf{v}}_{i}^{\mathrm{rel}}=-\overrightarrow{\mathbf{v}}_{f}^{\mathrm{rel}}$ (1− dimensional energy-momentum prinicple) .

Consequently the initial and final relative speeds are equal. We shall call this relationship between the relative initial and final velocities the one-dimensional energy-momentum principle because we have combined these two principles to realize this result. The energy-momentum principle is independent of the masses of the colliding particles.

Although we derived this result explicitly, we have already shown that the change in kinetic energy for a two-particle interaction (Equation (15.2.20)), in our simplified notation is given by

$$\Delta K=\frac{1}{2} \mu\left(\left(v^{\mathrm{rel}}\right)_{f}^{2}-\left(v^{\mathrm{rel}}\right)_{i}^{2}\right) \nonumber$$

Therefore for an elastic collision where $\Delta K=0$, the square of the relative speed remains constant

$$\left(v^{\mathrm{rel}}\right)_{f}^{2}=\left(v^{\mathrm{rel}}\right)_{i}^{2} \nonumber$$

For a one-dimensional collision, the magnitude of the relative speed remains constant but the direction changes by $180^{\circ}$.

We can now solve for the final x -component of the velocities, $v_{1 x, f}$ and $\mathcal{V}_{2 x, f}$ as follows. Equation (15.3.7) may be rewritten as

$$v_{2 x, f}=v_{1 x, f}+v_{1 x, i}-v_{2 x, i} \nonumber$$

Now substitute Equation (15.3.12) into Equation (15.3.1) yielding

$$m_{1} v_{1 x, i}+m_{2} v_{2 x, i}=m_{1} v_{1 x, f}+m_{2}\left(v_{1 x, f}+v_{1 x, i}-v_{2 x, i}\right) \nonumber$$

Solving Equation (15.3.13) for $v_{1 x, f}$ involves some algebra and yields

$$v_{1 x, f}=\frac{m_{1}-m_{2}}{m_{1}+m_{2}} v_{1 x, i}+\frac{2 m_{2}}{m_{1}+m_{2}} v_{2 x, i} \nonumber$$

To find $v_{2 x, f}$, rewrite Equation (15.3.7) as

$$v_{1 x, f}=v_{2 x, f}-v_{1 x, i}+v_{2 x, i} \nonumber$$

Now substitute Equation (15.3.15) into Equation (15.3.1) yielding

$$m_{1} v_{1 x, i}+m_{2} v_{2 x, i}=m_{1}\left(v_{2 x, f}-v_{1 x, i}+v_{2 x, i}\right) v_{1 x, f}+m_{2} v_{2 x, f} \nonumber$$

We can solve Equation (15.3.16) for $v_{2 x, f}$ and determine that

$$v_{2 x, f}=v_{2 x, i} \frac{m_{2}-m_{1}}{m_{2}+m_{1}}+v_{1 x, i} \frac{2 m_{1}}{m_{2}+m_{1}} \nonumber$$

Consider what happens in the limits $m_{1} \gg m_{2}$ in Equation (15.3.14). Then

$$v_{1 x, f} \rightarrow v_{1 x, i}+\frac{2}{m_{1}} m_{2} v_{2 x, i} \nonumber$$

the more massive object’s velocity component is only slightly changed by an amount proportional to the less massive object’s x -component of momentum. Similarly, the less massive object’s final velocity approaches

$$v_{2 x, f} \rightarrow-v_{2 x, i}+2 v_{1 x, i}=v_{1 x, i}+v_{1 x, i}-v_{2 x, i} \nonumber$$

We can rewrite this as

$$v_{2 x, f}-v_{1 x, i}=v_{1 x, i}-v_{2 x, i}=v_{x, i}^{\mathrm{rel}} \nonumber$$

i.e. the less massive object “rebounds” with the same speed relative to the more massive object which barely changed its speed.

If the objects are identical, or have the same mass, Equations (15.3.14) and (15.3.17) become

$$v_{1 x, f}=v_{2 x, i}, \quad v_{2 x, f}=v_{1 x, i} \nonumber$$

the objects have exchanged x -components of velocities, and unless we could somehow distinguish the objects, we might not be able to tell if there was a collision at all.

One-Dimensional Collision Between Two Objects – Center-of-Mass Reference Frame

We analyzed the one-dimensional elastic collision (Figure 15.5) in Section 15.4.1 in the laboratory reference frame. Now let’s view the collision from the center-of-mass (CM) frame. The x -component of velocity of the center-of-mass is

$$v_{x, \mathrm{cm}}=\frac{m_{1} v_{1 x, i}+m_{2} v_{2 x, i}}{m_{1}+m_{2}} \nonumber$$

With respect to the center-of-mass, the x -components of the velocities of the objects are

$$\begin{array}{l} v_{1 x, i}^{\prime}=v_{1 x, i}-v_{x, \mathrm{cm}}=\left(v_{1 x, i}-v_{2 x, i}\right) \frac{m_{2}}{m_{1}+m_{2}} \\ v_{2 x, i}^{\prime}=v_{2 x, i}-v_{x, \mathrm{cm}}=\left(v_{2 x, i}-v_{1 x, i}\right) \frac{m_{1}}{m_{1}+m_{2}} \end{array} \nonumber$$

In the CM frame the momentum of the system is zero before the collision and hence the momentum of the system is zero after the collision. For an elastic collision, the only way for both momentum and kinetic energy to be the same before and after the collision is either the objects have the same velocity (a miss) or to reverse the direction of the velocities as shown in Figure 15.6.

Figure 15.6 One-dimensional elastic collision in center-of-mass reference frame

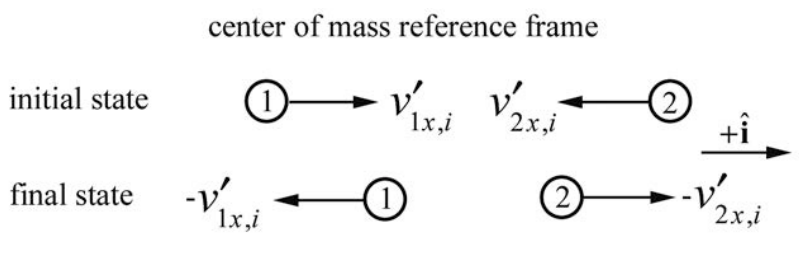
In the CM frame, the final x -components of the velocities are

$$\begin{array}{l} v_{1 x, f}^{\prime}=-v_{1 x, i}^{\prime}=\left(v_{2 x, i}-v_{1 x, i}\right) \frac{m_{2}}{m_{1}+m_{2}} \\ v_{2 x, f}^{\prime}=-v_{2 x, i}^{\prime}=\left(v_{2 x, i}-v_{1 x, i}\right) \frac{m_{1}}{m_{1}+m_{2}} \end{array} \nonumber$$

The final x -components of the velocities in the “laboratory frame” are then given by

$$\begin{aligned} v_{1 x, f} &=v_{1 x, f}^{\prime}+v_{x, \mathrm{cm}} \\ &=\left(v_{2 x, i}-v_{1 x, i}\right) \frac{m_{2}}{m_{1}+m_{2}}+\frac{m_{1} v_{1 x, i}+m_{2} v_{2 x, i}}{m_{1}+m_{2}} \\ &=v_{1 x, i} \frac{m_{1}-m_{2}}{m_{1}+m_{2}}+v_{2 x, i} \frac{2 m_{2}}{m_{1}+m_{2}} \end{aligned} \nonumber$$

as in Equation (15.3.14) and a similar calculation reproduces Equation (15.3.17).