15.5: Worked Examples

Example 15.1 Elastic One-Dimensional Collision Between Two Objects

Figure 15.7 Elastic collision between two non-identical carts

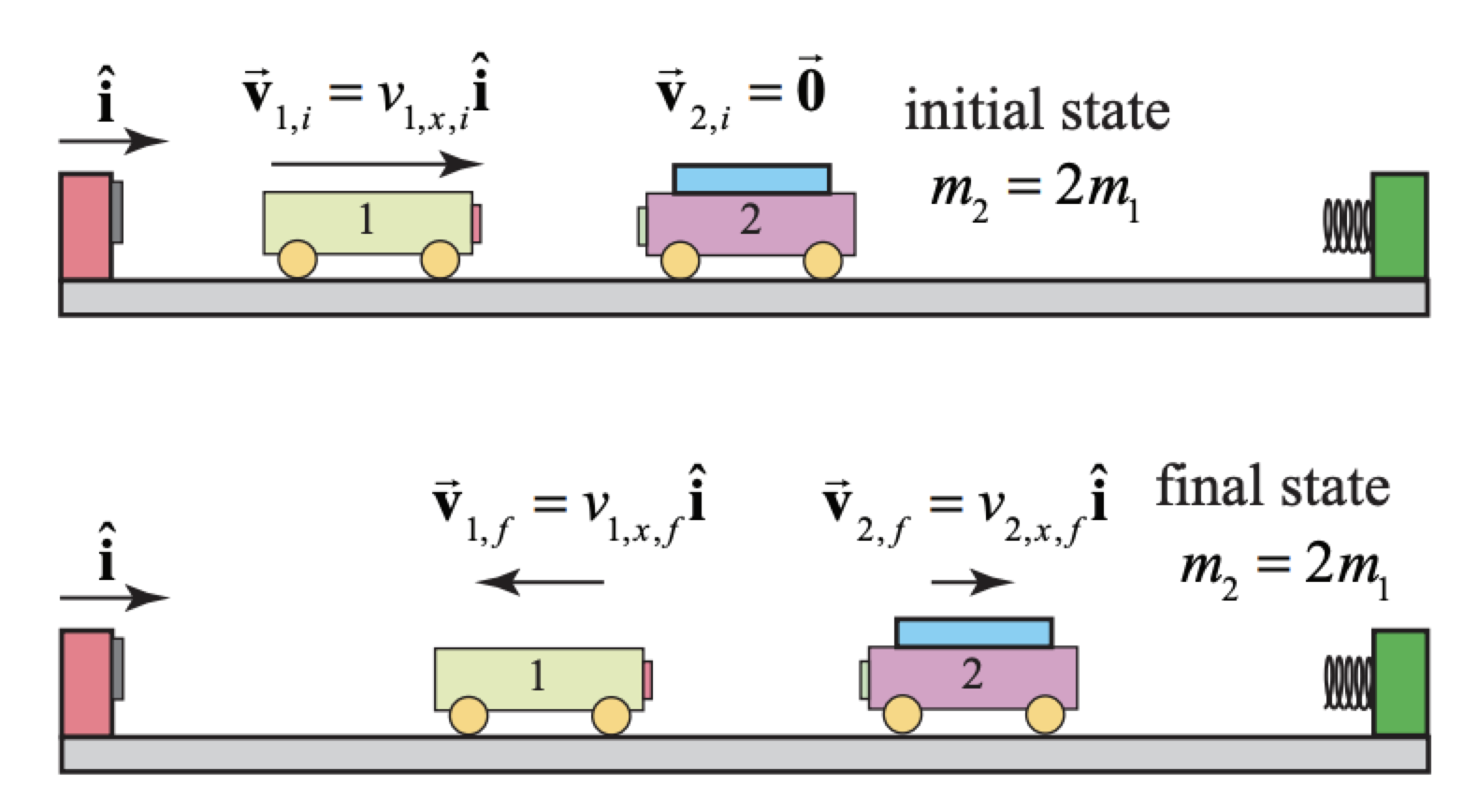
Consider the elastic collision of two carts along a track; the incident cart 1 has mass \(m_{1}\ and moves with initial speed \(v_{1,i}\). The target cart has mass \(m_{2}=2 m_{1}\) and is initially at rest, \(v_{2, i}=0\), (Figure 15.7). Immediately after the collision, the incident cart has final speed \(v_{1, f}\) and the target cart has final speed \(v_{2, f}\). Calculate the final x-component of the velocities of the carts as a function of the initial speed \(v_{1, i}\).

Solution: The momentum flow diagram for the objects before (initial state) and after (final state) the collision are shown in Figure 15.7. We can immediately use our results above with \(m_{2}=2 m_{1}\) and \(v_{2, i}=0\). The final x -component of velocity of cart 1 is given by Equation (15.3.14), where we use \(v_{1 x, i}=v_{1, i}\).

\[v_{1 x, f}=-\frac{1}{3} v_{1, i} \nonumber \] The final x-component of velocity of cart 2 is given by Equation (15.4.17) \[v_{2 x, f}=\frac{2}{3} v_{1, i} \nonumber \]

Example 15.2 The Dissipation of Kinetic Energy in a Completely Inelastic Collision Between Two Objects

Figure 15.7b Inelastic collision between two non-identical carts

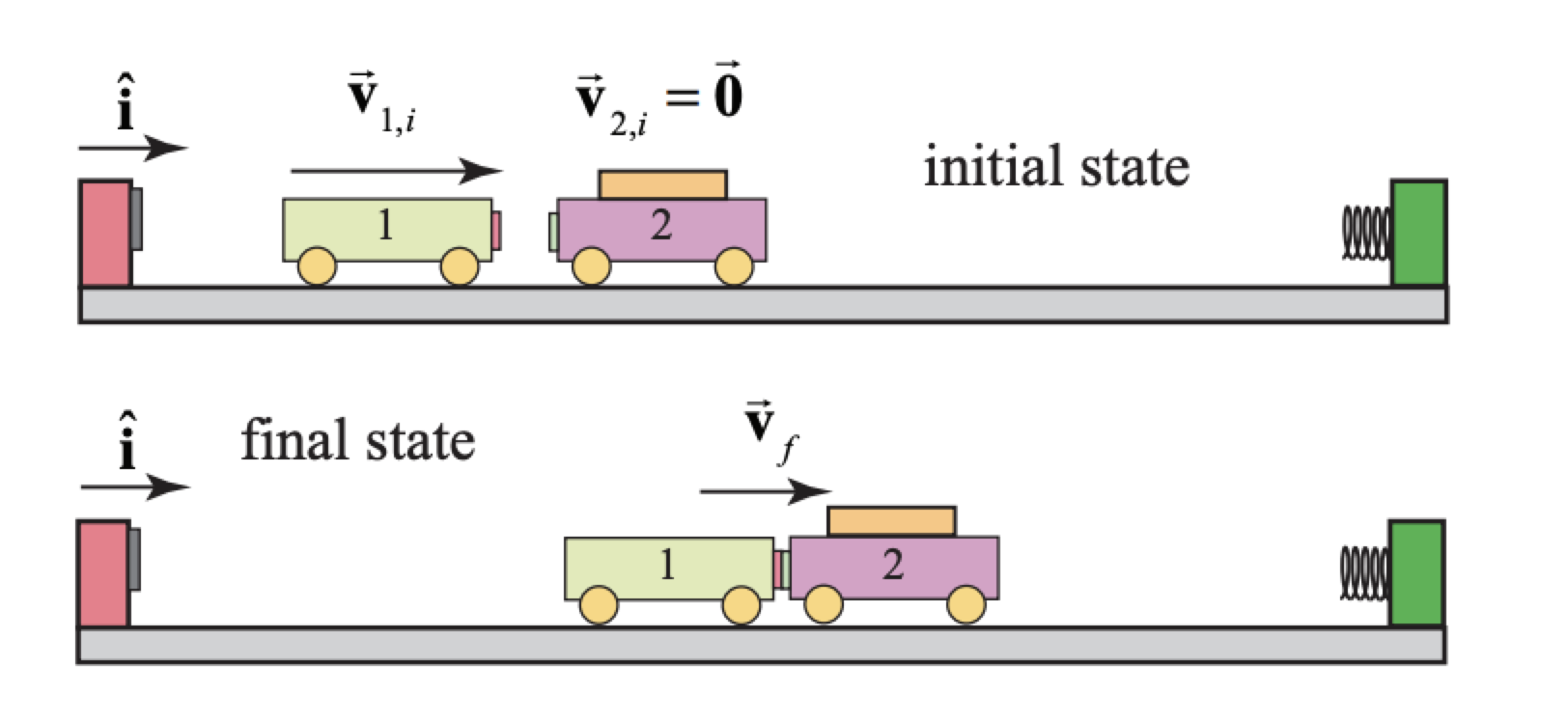
An incident cart of mass \(m_{1}\) and initial speed \(v_{1,i}\) collides completely inelastically with a cart of mass \(m_{2}\) that is initially at rest (Figure 15.7b). There are no external forces acting on the objects in the direction of the collision. Find \(\Delta K / K_{\text {initial }}=\left(K_{\text {final }}-K_{\text {initial }}\right) / K_{\text {initial }}\)

Solution: In the absence of any net force on the system consisting of the two carts, the momentum after the collision will be the same as before the collision. After the collision, the carts will move in the direction of the initial velocity of the incident cart with a common speed \(v_{f}\) found from applying the momentum condition

\[m_{1} v_{1, i}=\left(m_{1}+m_{2}\right) v_{f} \Rightarrow v_{f}=\frac{m_{1}}{m_{1}+m_{2}} v_{1, i} \nonumber \] The initial relative speed is \(v_{i}^{\mathrm{rel}}=v_{1, i}\). The final relative velocity is zero because the carts stick together so using Equation (15.3.26), the change in kinetic energy is \[\Delta K=-\frac{1}{2} \mu\left(v_{i}^{r e l}\right)^{2}=-\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{1, i}^{2} \nonumber \] The ratio of the change in kinetic energy to the initial kinetic energy is then \[\Delta K / K_{\text {initial}}=-\frac{m_{2}}{m_{1}+m_{2}} \nonumber \] As a check, we can calculate the change in kinetic energy via \[\Delta K=\left(K_{f}-K_{i}\right)=\frac{1}{2}\left(m_{1}+m_{2}\right) v_{f}^{2}-\frac{1}{2} v_{1, i}^{2} =\frac{1}{2}\left(m_{1}+m_{2}\right)\left(\frac{m_{1}}{m_{1}+m_{2}}\right)^{2} v_{1, i}^{2}-\frac{1}{2} v_{1, i}^{2} =\left(\frac{m_{1}}{m_{1}+m_{2}}-1\right)\left(\frac{1}{2} m_{1} v_{1, i}^{2}\right)=-\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{1, i}^{2} \nonumber \]

in agreement with Equation (15.4.4).

Example 15.3 Bouncing Superballs

Figure 15.8b Two superballs dropping

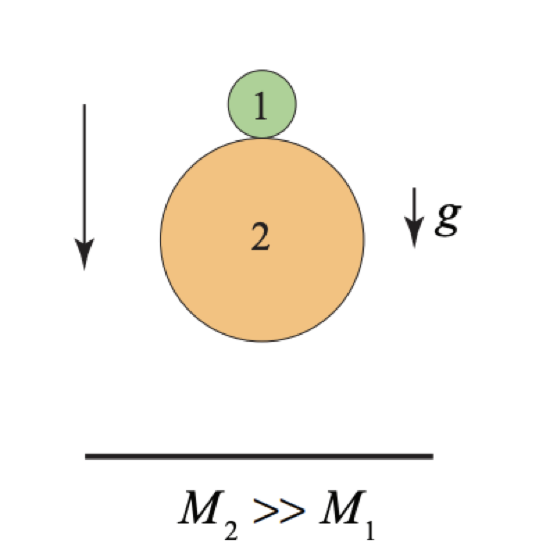
Consider two balls that are dropped from a height \(h_{i}\) above the ground, one on top of the other (Figure 15.8). Ball 1 is on top and has mass \(M_{1}\), and ball 2 is underneath and has mass \(M_{2}\) with \(M_{2}>>M_{1}\). Assume that there is no loss of kinetic energy during all collisions. Ball 2 first collides with the ground and rebounds. Then, as ball 2 starts to move upward, it collides with the ball 1 which is still moving downwards (figure below left). How high will ball 1 rebound in the air? Hint: consider this collision as seen by an observer moving upward with the same speed as the ball 2 has after it collides with the ground. What speed does ball 1 have in this reference frame after it collides with the ball 2?

Solution

The system consists of two balls and the earth. There are five special states for this motion shown in the figure below.

part a)

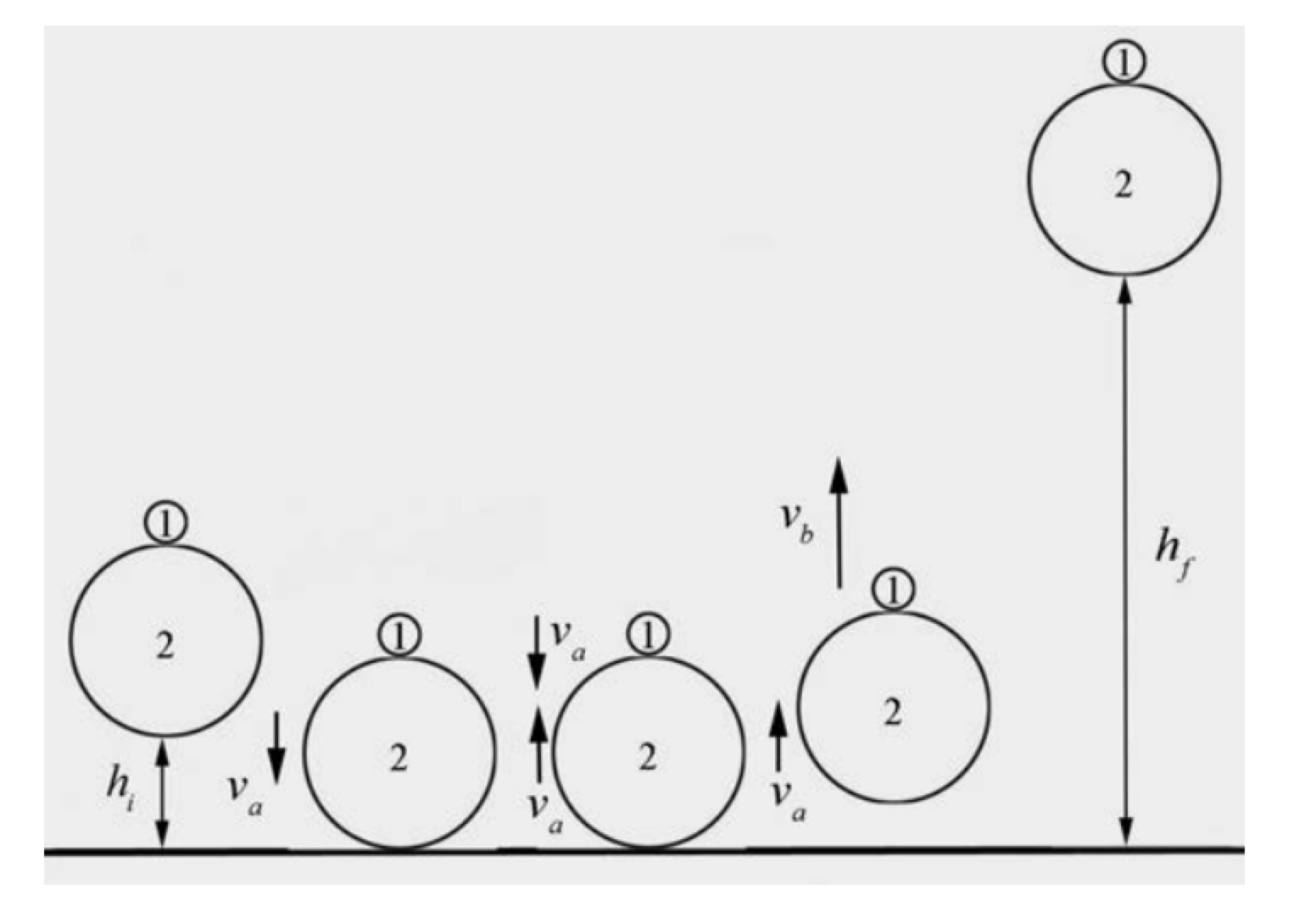
Initial State: the balls are released from rest at a height \(h_{i}\) above the ground.

State A: the balls just reach the ground with speed \(v_{a}=\sqrt{2 g h_{i}}\). This follows from \(\Delta E_{\text {mесh}}=0 \Rightarrow \Delta K=-\Delta U\). Thus \((1 / 2) m v_{a}^{2}-0=-m g \Delta h=m g h_{i} \Rightarrow v_{a}=\sqrt{2 g h_{i}}\)

State B: immediately before the collision of the balls. Ball 2 has collided with the ground and reversed direction with the same speed, \(v_{a}\) but ball 1 is still moving downward with speed \(v_{a}\).

State C: immediately after the collision of the balls. Because we are assuming that \(m_{2} \gg m_{1}\) ball 2 does not change its speed as a result of the collision so it is still moving 2 upward with speed \(v_{a}\). As a result of the collision, ball 1 moves upward with speed \(v_{b}\)

Final State: ball 1 reaches a maximum height \(h_{f}=v_{b}^{2} / 2 g\) above the ground. This again follows from \(\Delta K=-\Delta U \Rightarrow 0-(1 / 2) m v_{b}^{2}=-m g \Delta h=-m g h_{f} \Rightarrow h_{f}=v_{b}^{2} / 2 g\)

Choice of Reference Frame:

As indicated in the hint above, this collision is best analyzed from the reference frame of an observer moving upward with speed \(v_{a}\) the speed of ball 2 just after it rebounded with the ground. In this frame immediately, before the collision, ball 1 is moving downward with a speed \(v_{b}^{\prime}\) that is twice the speed seen by an observer at rest on the ground (lab reference frame). \[v_{a}^{\prime}=2 v_{a} \nonumber \]

The mass of ball 2 is much larger than the mass of ball 1, \(m_{2} \gg m_{1}\) This enables us to consider the collision (between States B and C) to be equivalent to ball 1 bouncing off a hard wall, while ball 2 experiences virtually no recoil. Hence ball 2 remains at rest in the reference frame moving upwards with speed \(\mathcal{V}_{a}\) with respect to observer at rest on ground. Before the collision, ball 1 has speed \(v_{a}^{\prime}=2 v_{a}\) Since there is no loss of kinetic energy during the collision, the result of the collision is that ball 1 changes direction but maintains the same speed, \[v_{b}^{\prime}=2 v_{a} \nonumber \] However, according to an observer at rest on the ground, after the collision ball 1 is moving upwards with speed \[v_{b}=2 v_{a}+v_{a}=3 v_{a} \nonumber \] While rebounding, the mechanical energy of the smaller superball is constant (we consider the smaller superball and the Earth as a system) hence between State C and the Final State, \[\Delta K+\Delta U=0 \nonumber \] The change in kinetic energy is \[\Delta K=-\frac{1}{2} m_{1}\left(3 v_{a}\right)^{2} \nonumber \] The change in potential energy is \[\Delta U=m_{1} g h_{f} \nonumber \] So the condition that mechanical energy is constant (Equation (15.5.10)) is now \[-\frac{1}{2} m_{1}\left(3 v_{1 a}\right)^{2}+m_{1} g h_{f}=0 \nonumber \] We can rewrite Equation (15.5.13) as \[m_{1} g h_{f}=9 \frac{1}{2} m_{1}\left(v_{a}\right)^{2} \nonumber \] Recall that we can also use the fact that the mechanical energy doesn’t change between the Initial State and State A yielding an equation similar to Equation (15.5.14), \[m_{1} g h_{i}=\frac{1}{2} m_{1}\left(v_{a}\right)^{2} \nonumber \] Now substitute the expression for the kinetic energy in Equation (15.5.15) into Equation (15.5.14) yielding \[m_{1} g h_{f}=9 m_{1} g h_{i} \nonumber \] Thus ball 1 reaches a maximum height \[h_{f}=9 h_{i} \nonumber \]