27.4: Pascal’s Law - Pressure as a Function of Depth in a Fluid of Uniform Density in a Uniform Gravitational Field

Consider a static fluid of uniform density \(rho\). Choose a coordinate system such that the z - axis points vertical downward and the plane z = 0 is at the surface of the fluid. Choose an infinitesimal cylindrical volume element of the fluid at a depth z , cross-sectional area A and thickness dz as shown in Figure 27.3. The volume of the element is \(d V=A d z\) and the mass of the fluid contained within the element is \(d m=\rho A d z\).

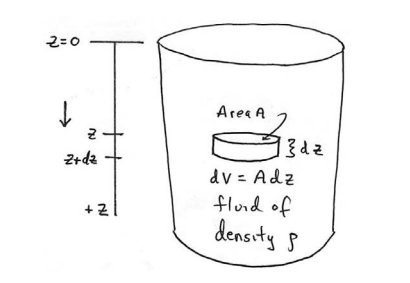Figure 27.2: Coordinate system for fluid

The surface of the infinitesimal fluid cylindrical element has three faces, two caps and the cylindrical body. Because the fluid is static the force due to the fluid pressure points inward on each of these three faces. The forces on the cylindrical surface add to zero. On the end-cap at z , the force due to pressure of the fluid above the end-cap is downward, \(\overrightarrow{\mathbf{F}}(z)=F(z) \hat{\mathbf{k}}\) where F(z) is the magnitude of the force. On the end-cap at z + dz , the force due to the pressure of the fluid below the end-cap is upward,\(\overrightarrow{\mathbf{F}}(z+d z)=-F(z+d z) \hat{\mathbf{k}}\) where \(F(z+d z)\) is the magnitude of the force. The gravitational force acting on the element is given by \(\overrightarrow{\mathbf{F}}^{g}=(d m) g \hat{\mathbf{k}}=(\rho d V) g \hat{\mathbf{k}}=\rho A d z g \hat{\mathbf{k}}\). There are also radial inward forces on the cylindrical body which sum to zero. The free body force diagram on the element is shown in Figure 27.3.

Figure 27.3: Free-body force diagram on cylindrical fluid element

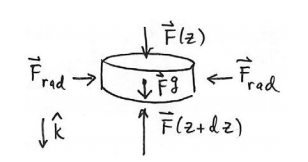
The vector sum of the forces is zero because the fluid is static (Newton’s Second Law). Therefore in the \(+\hat{\mathbf{k}}\) \[F(z)-F(z+d z)+\rho A d z g=0 \nonumber \] a result known as Pascal’s Law.

Example 27.1 Pressure in the Earth's Ocean

What is the change in pressure between a depth of 4 km and the surface in Earth’s ocean?

Solution

We begin by assuming the density of water is uniform in the ocean, and so we can use Pascal’s Law, Eq. (27.4.7) to determine the pressure, where we use \(\rho=1.03 \times 10^{3} \mathrm{kg} \cdot \mathrm{m}^{-3}\) for the density of seawater (Table 27.1). Then \[\begin{array}{l}
P(z)-P(z=0)=\rho g z \\
=\left(1.03 \times 10^{3} \mathrm{kg} \cdot \mathrm{m}^{-3}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)\left(4 \times 10^{3} \mathrm{m}\right) \\
=40 \times 10^{6} \mathrm{Pa}
\end{array} \nonumber \]

Example 27.2 Pressure in a Rotating Sample in a Centrifuge

In an ultra centrifuge, a liquid filled chamber is spun with a high angular speed ω about a fixed axis. The density ρ of the fluid is uniform. The open-ended side of the chamber is a distance \(r_{o}\) from the fixed axis. The chamber has cross sectional area A and of length L , (Figure 27.4).

Figure 27.4: Schematic representation of centrifuge

The chamber is spinning fast enough to ignore the effect of gravity. Determine the pressure in the fluid as a function of distance r from the fixed axis.

Solution

Choose polar coordinates in the plane of circular motion. Consider a small volume element of the fluid of cross-sectional area A , thickness dr , and mass \(d M=\rho A d r\) that is located a distance r from the fixed axis. Denote the pressure at one end of the volume element by \(P(r)=F(r) / A\) and the pressure at the other end by \(P(r+d r)=F(r+d r) / A\). The free-body force diagram on the volume fluid element is shown in Figure 27.5.

Figure 27.5: Free-body force diagram showing only radial forces on fluid element in centrifuge

The element is accelerating inward with radial component of the acceleration, \(a_{r}=-r \omega^{2}\). Newton’s Second Law applied to the fluid element is then \[(P(r)-P(r+d r)) A=-(\rho A d r) r \omega^{2} \nonumber \] We can rewrite Eq. (27.4.9) as \[\frac{P(r+d r)-P(r)}{d r}=\rho r \omega^{2} \nonumber \] and take the limit dr → 0 resulting in \[\frac{d P}{d r}=\rho r \omega^{2} \nonumber \] We can integrate Eq. (27.4.11) between an arbitrary distance r from the rotation axis and the open-end located at \(R_{O}\), where the pressure \(P\left(r_{0}\right)=1 \mathrm{atm}\). \[\int_{P(r)}^{P\left(r_{0}\right)} d P=\rho \omega^{2} \int_{r=r}^{r^{\prime}=r_{0}} r^{\prime} d r^{\prime} \nonumber \] Integration yields \[P\left(r_{0}\right)-P(r)=\frac{1}{2} \rho \omega^{2}\left(r_{0}^{2}-r^{2}\right) \nonumber \] The pressure at a distance r from the rotation axis is then \[P(r)=P\left(r_{0}\right)+\frac{1}{2} \rho \omega^{2}\left(r^{2}-r_{0}^{2}\right) \nonumber \]