1.6: The Theorems of Pappus

(Pappus Alexandrinus, Greek mathematician, approximately 3rd or 4th century AD.)

1. If a plane area is rotated about an axis in its plane, but which does not cross the area, the volume swept out equals the area times the distance moved by the centroid.
2. If a plane curve is rotated about an axis in its plane, but which does not cross the curve, the area swept out equals the length times the distance moved by the centroid.

These theorems enable us to work out the volume of a solid of revolution if we know the position of the centroid of a plane area, or vice versa; or to work out the area of a surface of revolution if we know the position of the centroid of a plane curve or vice versa. It is not necessary that the plane or the curve be rotated through a full 360^o.

We prove the theorems first. We then follow with some examples.

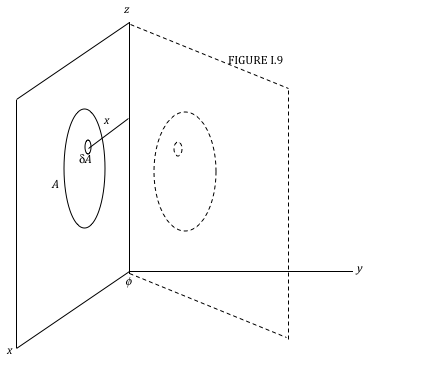
Consider an area $A$ in the $zx$ plane (Figure I.9), and an element $\delta A$ within the area at a distance $x$ from the $z$ axis. Rotate the area through an angle $\phi$ about the $z$ axis. The length of the arc traced by the element $dA$ in moving through an angle $\phi$ is $x \phi$ , so the volume swept out by $\delta A$ is $x \phi \delta A$. The volume swept out by the entire area is $\phi$ $\int xd A$. But the definition of the centroid of $A$ is such that its distance from the $z$ axis is given by $\overline{x} A$ = $\int x d A$. Therefore the volume swept out by the area is $\phi \overline{x} A$. But $\phi \overline{x}$ is the distance moved by the centroid, so the first theorem of Pappus is proved.

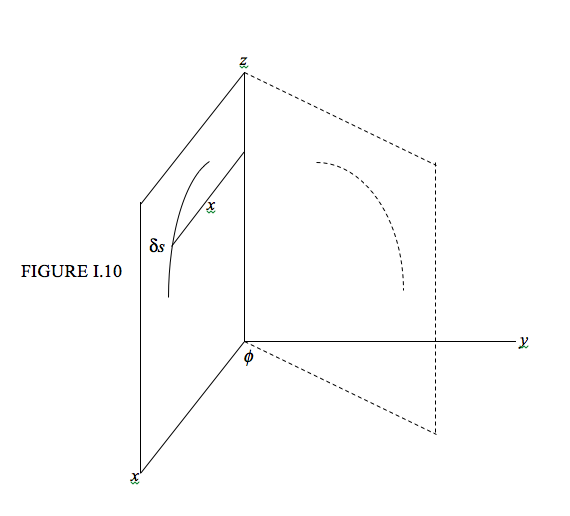
Consider a curve of length $L$ in the $zx$ plane (Figure I.10), and an element $\delta s$ of the curve at a distance $x$ from the $z$ axis. Rotate the curve through an angle $\phi$ about the $z$ axis. The length of the arc traced by the element $\delta s$in moving through an angle $\phi$ is $x\phi$, so the area swept out by $\delta s$ is $x \phi \delta s$. The area swept out by the entire curve is $\phi \int x ds$ . But the definition of the centroid is such that its distance from the $z$ axis is given by $\overline{x}L = \int xds$. Therefore the area swept out by the curve is $\phi \overline{x} L$. But $\phi \overline{x}$ is the distance moved by the centroid, so the second theorem of Pappus is proved.

Applications of the Theorems of Pappus

Rotate a plane semicircular figure of area $\frac{1}{2} \pi a^{2}$ through 360^o about its diameter. The volume swept out is $\frac{4}{3} \pi a^{3}$ , and the distance moved by the centroid is $2 \pi \overline{x}$ Therefore by the theorem of Pappus, $\overline{x} = \frac{4a}{(3 \pi )}$.

Rotate a plane semicircular arc of length π a through 360^o about its diameter. Use a similar argument to show that $\overline{x} = \frac{2a} { \pi}$.

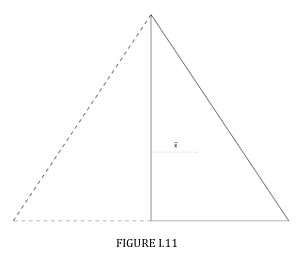
Consider a right-angled triangle, height $h$, base $a$ (Figure I.11). Its centroid is at a distance $\frac{a}{3}$ from the height $h$. The area of the triangle is $\frac{ah}{2}$. Rotate the triangle through 360^o about $h$. The distance moved by the centroid is $\frac{2 \pi a}{3}$. The volume of the cone swept out is $\frac{ah}{2}$ times $\frac{2 \pi}{3}$, equals $\frac{ \pi a^{2} h}{3}$.

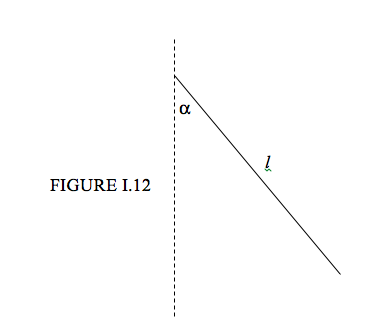
Now consider a line of length $l$ inclined at an angle $\alpha$ to the $y$ axis (Figure I.12). Its centroid is at a distance $\frac{1}{2} l \sin \alpha$ from the $y$ axis. Rotate the line through 360^o about the $y$ axis. The distance moved by the centroid is $2 \pi \times \frac{1}{2} l \sin \alpha = \pi l \sin \alpha$. The surface area of the cone swept out is $l \times\pi\ l \sin \alpha =\pi l^{2} \sin \alpha$.

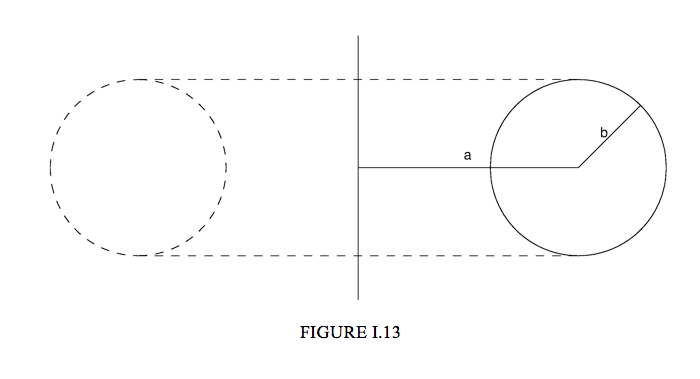
The centre of a circle of radius $b$ is at a distance $a$ from the $y$ axis. It is rotated through 360^o about the $y$ axis to form a torus (Figure I.13). Use the theorems of Pappus to show that the volume and surface area of the torus are, respectively, $2 \pi ^{2} ab^{2}$ and $4 \pi ^{2} ab$ .