6.5: Angular Velocity and Angular Acceleration

. Angular Velocity

We shall always choose a right-handed cylindrical coordinate system. If the positive z - axis points up, then we choose θ to be increasing in the counterclockwise direction as shown in Figures 6.6.

Figure 6.6 Right handed coordinate system

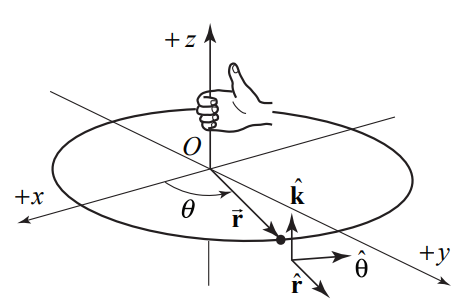
For a point object undergoing circular motion about the z -axis, the angular velocity vector \(\vec{\omega}\) is directed along the z -axis with z -component equal to the time derivative of the angle θ,

\[\vec{\omega}=\frac{d \theta}{d t} \hat{\mathbf{k}}=\omega_{z} \hat{\mathbf{k}} \nonumber \]

The SI units of angular velocity are \(\left[\mathrm{rad} \cdot \mathrm{s}^{-1}\right]\) Note that the angular speed is just the magnitude of the z -component of the angular velocity,

\[\omega \equiv\left|\omega_{z}\right|=\left|\frac{d \theta}{d t}\right| \nonumber \]

If the velocity of the object is in the \(+\hat{\boldsymbol{\theta}}\)-direction, (rotating in the counterclockwise direction in Figure 6.7(a)), then the z -component of the angular velocity is positive, \(\omega_{z}=d \theta / d t>0\) The angular velocity vector then points in the \(+\hat{\mathbf{k}}\)-direction as shown in Figure 6.7(a). If the velocity of the object is in the \(-\hat{\boldsymbol{\theta}}\)-direction, (rotating in the clockwise direction in Figure 6.7(b)), then the z -component of the angular velocity angular velocity is negative, \(\omega_{z}=d \theta / d t<0\). The angular velocity vector then points in the \(-\hat{\mathbf{k}}\)-direction as shown in Figure 6.7(b).

Figure 6.7(b) Angular velocity vector for motion with dθ / dt > 0 .

Figure 6.7(b) Angular velocity for motion with dθ / dt < 0 .

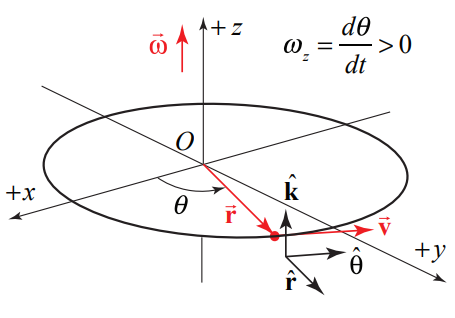
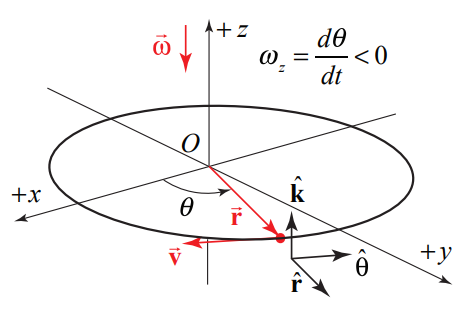
The velocity and angular velocity are related by

\[\overrightarrow{\mathbf{v}}=\overrightarrow{\boldsymbol{\omega}} \times \overrightarrow{\mathbf{r}}=\frac{d \theta}{d t} \hat{\mathbf{k}} \times r \hat{\mathbf{r}}=r \frac{d \theta}{d t} \hat{\boldsymbol{\theta}} \nonumber \]

Example 6.2 Angular Velocity

A particle is moving in a circle of radius R. At t = 0 , it is located on the x -axis. The angle the particle makes with the positive x -axis is given by \(\theta(t)=A t-B t^{3}\) where A and B are positive constants. Determine (a) the angular velocity vector, and (b) the velocity vector. Express your answer in polar coordinates. (c) At what time, \(t=t_{1}\) is the angular velocity zero? (d) What is the direction of the angular velocity for 1. \(t<t_{1}\) 2. \(t>t_{1} ?\)?

Solution:

The derivative of \(\theta(t)=A t-B t^{3}\) is

\[\frac{d \theta(t)}{d t}=A-3 B t^{2} \nonumber \]

Therefore the angular velocity vector is given by

\[\overrightarrow{\boldsymbol{\omega}}(t)=\frac{d \theta(t)}{d t} \hat{\mathbf{k}}=\left(A-3 B t^{2}\right) \hat{\mathbf{k}} \nonumber \]

The velocity is given by

\[\overrightarrow{\mathbf{v}}(t)=R \frac{d \theta(t)}{d t} \hat{\mathbf{\theta}}(t)=R\left(A-3 B t^{2}\right) \hat{\boldsymbol{\theta}}(t) \nonumber \]

The angular velocity is zero at time \(t=t_{1}\) when

\[A-3 B t_{1}^{2}=0 \Rightarrow t_{1}=\sqrt{A / 3 B} \nonumber \]

For \(t<t_{1}, \frac{d \theta(t)}{d t}=A-3 B t_{1}^{2}>0\) hence \(\overrightarrow{\boldsymbol{\omega}}(t)\) points in the positive \(\hat{\mathbf{k}}\)-direction.

For \(t>t_{1}, \frac{d \theta(t)}{d t}=A-3 B t_{1}^{2}<0\) hence \(\overrightarrow{\boldsymbol{\omega}}(t)\) points in the positive \(\hat{\mathbf{k}}\)-direction.

Angular Acceleration

In a similar fashion, for a point object undergoing circular motion about the fixed z -axis, the angular acceleration is defined as

\[\vec{\alpha}=\frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}}=\alpha_{z} \hat{\mathbf{k}} \nonumber \]

The SI units of angular acceleration are \(\left[\mathrm{rad} \cdot \mathrm{s}^{-2}\right]\) The magnitude of the angular acceleration is denoted by the Greek symbol alpha,

\[\alpha \equiv|\vec{\alpha}|=\left|\frac{d^{2} \theta}{d t^{2}}\right| \nonumber \]

There are four special cases to consider for the direction of the angular velocity. Let’s first consider the two types of motion with \(\overrightarrow{\boldsymbol{\alpha}}\) pointing in the \(\hat{\mathbf{k}}\)-direction: (i) if the object is rotating counterclockwise and speeding up then both \(d \theta / d t>0\) and \(d^{2} \theta / d t^{2}>0\) (Figure 6.8(a)) (ii) if the object is rotating clockwise and slowing down then \(d \theta / d t<0\) but \(d^{2} \theta / d t^{2}>0\) (Figure 6.8(b). There are two corresponding cases in which \(\vec{\alpha}\) pointing in the \(-\hat{\mathbf{k}}\)-direction (iii) if the object is rotating counterclockwise and slowing down then \(d \theta / d t>0\) but \(d^{2} \theta / d t^{2}<0\) (Figure 6.9(a), (iv) if the object is rotating clockwise and speeding up then both \(d \theta / d t<0\) and \(d^{2} \theta / d t^{2}<0\) (Figure 6.9(b).

Figure 6.8(a) Angular acceleration vector vector for motion with \(d \theta / d t>0\), and \(d^{2} \theta / d t^{2}>0\)

Figure 6.8(b) Angular velocity vector vector for motion with \(d \theta / d t<0\), and \(d^{2} \theta / d t^{2}>0\)

Figure 6.9(a) Angular acceleration vector vector for motion with \(d \theta / d t>0\), and \(d^{2} \theta / d t^{2}<0\)

Figure 6.9(b) Angular velocity vector vector for motion with \(d \theta / d t<0\), and \(d^{2} \theta / d t^{2}<0\)

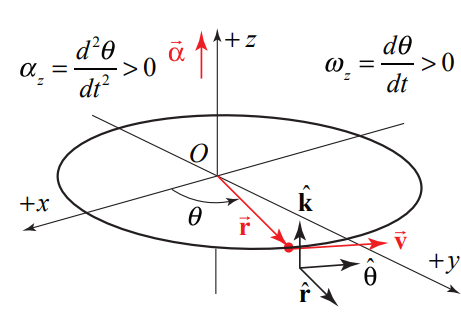
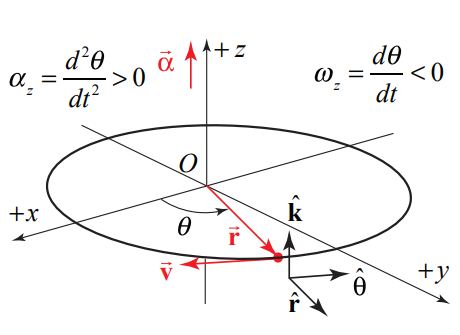
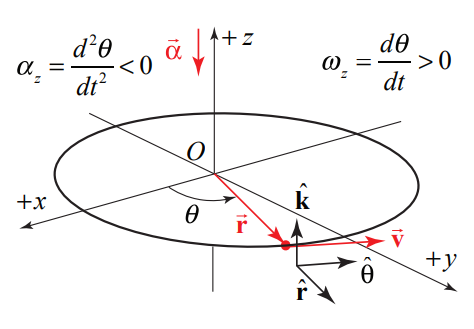
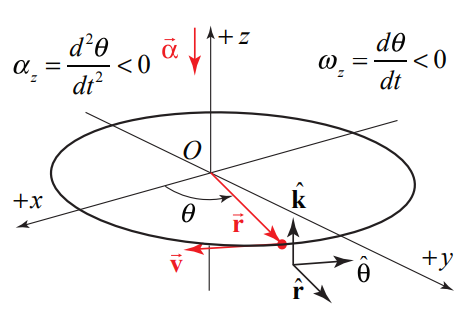
Example 6.3 Integration and Circular Motion Kinematics

A point-like object is constrained to travel in a circle. The z -component of the angular acceleration of the object for the time interval \(\left[0, t_{1}\right]\) is given by the function

\[\alpha_{z}(t)=\left\{\begin{array}{l}
b\left(1-\frac{t}{t_{1}}\right) ; 0 \leq t \leq t_{1} \\
0 ; t>t_{1}
\end{array}\right. \nonumber \]

where b is a positive constant with units rad\(\cdot \mathrm{S}^{-2}\).

a) Determine an expression for the angular velocity of the object at \(t=t_{1}\).

b) Through what angle has the object rotated at time \(t=t_{1}\)?

Solution:

a) The angular velocity at time \(t=t_{1}\) is given by

\[\omega_{z}\left(t_{1}\right)-\omega_{z}(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} \alpha_{z}\left(t^{\prime}\right) d t^{\prime}=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} b\left(1-\frac{t^{\prime}}{t_{1}}\right) d t^{\prime}=b\left(t_{1}-\frac{t_{1}^{2}}{2 t_{1}}\right)=\frac{b t_{1}}{2} \nonumber \]

b) In order to find the angle \(\theta\left(t_{1}\right)-\theta(t=0)\) that the object has rotated through at time \(t=t_{1}\), you first need to find \(\omega_{z}(t)\) by integrating the z-component of the angular acceleration

\[\omega_{z}(t)-\omega_{z}(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t} \alpha_{z}\left(t^{\prime}\right) d t^{\prime}=\int_{t=0}^{t^{\prime}=t} b\left(1-\frac{t^{\prime}}{t_{1}}\right) d t^{\prime}=b\left(t-\frac{t^{2}}{2 t_{1}}\right) \nonumber \]

Because it started from rest, \(\omega_{z}(t=0)=0\), hence \(\omega_{z}(t)=b\left(t-\frac{t^{2}}{2 t_{1}}\right) ; 0 \leq t \leq t_{1}\)

Then integrate \(\omega_{z}(t)\) between t = 0 and \(t=t_{1}\) to find that

\[\theta\left(t_{1}\right)-\theta(t=0)=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} \omega_{z}\left(t^{\prime}\right) d t^{\prime}=\int_{t^{\prime}=0}^{t^{\prime}=t_{1}} b\left(t^{\prime}-\frac{t^{\prime 2}}{2 t_{1}}\right) d t^{\prime}=b\left(\frac{t_{1}^{2}}{2}-\frac{t_{1}^{3}}{6 t_{1}}\right)=\frac{b t_{1}^{2}}{3} \nonumber \]