9.2: Universal Law of Gravitation and the Circular Orbit of the Moon
( \newcommand{\kernel}{\mathrm{null}\,}\)
An important example of (approximate) circular motion is the orbit of the Moon around the Earth. We can approximately calculate the time T the Moon takes to complete one circle around the earth (a calculation of great importance to early lunar calendar systems, which became the basis for our current model.) Denote the distance from the moon to the center of the earth by Re,m.
Because the Moon moves nearly in a circular orbit with angular speed ω=2π/T it is accelerating towards the Earth. The radial component of the acceleration (centripetal acceleration) is
ar=−4π2Re,mT2
According to Newton’s Second Law, there must be a centripetal force acting on the Moon directed towards the center of the Earth that accounts for this inward acceleration.
Universal Law of Gravitation
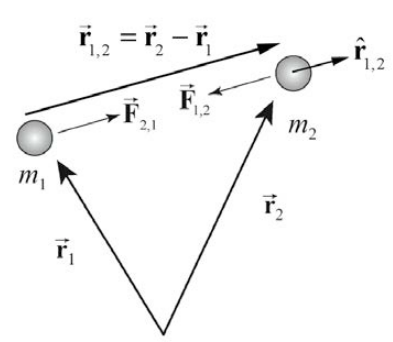
Newton’s Universal Law of Gravitation describes the gravitational force between two bodies 1 and 2 with masses m1 and m2 respectively. This force is a radial force (always pointing along the radial line connecting the masses) and the magnitude is proportional to the inverse square of the distance that separates the bodies. Then the force on object 2 due to the gravitational interaction between the bodies is given by,
→F1,2=−Gm1m2r21,2ˆr1,2
where r1,2 is the distance between the two bodies and ˆr1,2 is the unit vector located at the position of object 2 and pointing from object 1 towards object 2. The Universal Gravitation Constant is G=6.67×10−11N⋅m2⋅kg−2. Figure 9.1 shows the direction of the forces on bodies 1 and 2 along with the unit vector ˆr1,2.
Newton realized that there were still some subtleties involved. First, why should the mass of the Earth act as if it were all placed at the center? Newton showed that for a perfect sphere with uniform mass distribution, all the mass may be assumed to be located at the center. (This calculation is difficult and can be found in Appendix 9A to this chapter.) We assume for the present calculation that the Earth and the Moon are perfect spheres with uniform mass distribution.
Second, does this gravitational force between the Earth and the Moon form an action-reaction Third Law pair? When Newton first explained the Moon’s motion in 1666, he had still not formulated the Third Law, which accounted for the long delay in the publication of the Principia. The link between the concept of force and the concept of an action-reaction pair of forces was the last piece needed to solve the puzzle of the effect of gravity on planetary orbits. Once Newton realized that the gravitational force between any two bodies forms an action-reaction pair, and satisfies both the Universal Law of Gravitation and his newly formulated Third Law, he was able to solve the oldest and most important physics problem of his time, the motion of the planets.
The test for the Universal Law of Gravitation was performed through experimental observation of the motion of planets, which turned out to be resoundingly successful. For almost 200 years, Newton’s Universal Law was in excellent agreement with observation. A sign of more complicated physics ahead, the first discrepancy only occurred when a slight deviation of the motion of Mercury was experimentally confirmed in 1882. The prediction of this deviation was the first success of Einstein’s Theory of General Relativity (formulated in 1915).
We can apply this Universal Law of Gravitation to calculate the period of the Moon’s orbit around the Earth. The mass of the Moon is m1=7.36×1022 kg and the mass of the Earth is m2=5.98×1024kg. The distance from the Earth to the Moon is Re,m=3.82×108m. We show the force diagram in Figure 9.2.
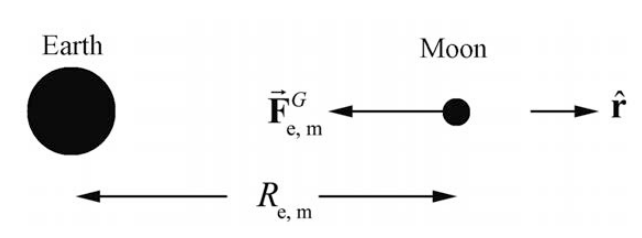
Newton’s Second Law of motion for the radial direction becomes
−Gm1m2R2e,m=−m14π2Re,mT2
We can solve this equation for the period of the orbit,
T=√4π2R3e,mGm2
Substitute the given values for the radius of the orbit, the mass of the earth, and the universal gravitational constant. The period of the orbit is
T=√4π2(3.82×108m)3(6.67×10−11N⋅m2⋅kg−2)(5.98×1024kg)=2.35×106s
This period is given in days by
T=(2.35×106s)(1 day 8.64×104s)=27.2 days
This period is called the sidereal month because it is the time that it takes for the Moon to return to a given position with respect to the stars.
The actual time T1 between full moons, called the synodic month (the average period of the Moon’s revolution with respect to the earth and is 29.53 days, it may range between 29.27 days and 29.83 days), is longer than the sidereal month because the Earth is traveling around the Sun. So for the next full moon, the Moon must travel a little farther than one full circle around the Earth in order to be on the other side of the Earth from the Sun (Figure 9.3).
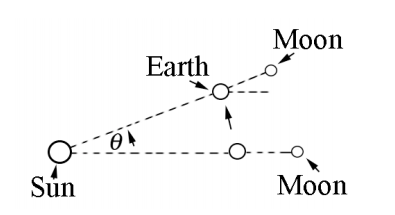
Therefore the time T1 between consecutive full moons is approximately T1≃T+ΔT where ΔT≃T/12=2.3
Kepler’s Third Law and Circular Motion
The first thing that we notice from the above solution is that the period does not depend on the mass of the Moon. We also notice that the square of the period is proportional to the cube of the distance between the Earth and the Moon,
T2=4π2R3e,mGm2
This is an example of Kepler’s Third Law, of which Newton was aware. This confirmation was convincing evidence to Newton that his Universal Law of Gravitation was the correct mathematical description of the gravitational force law, even though he still could not explain what “caused” gravity.


