13.4: Work done by Constant Forces
( \newcommand{\kernel}{\mathrm{null}\,}\)
We will begin our discussion of the concept of work by analyzing the motion of an object in one dimension acted on by constant forces. Let’s consider the following example: push a cup forward with a constant force along a desktop. When the cup changes velocity (and hence kinetic energy), the sum of the forces acting on the cup must be non-zero according to Newton’s Second Law. There are three forces involved in this motion: the applied pushing force →Fa; the contact force →C≡→N+→fk; and gravity →Fg=m→g. The force diagram on the cup is shown in Figure 13.2.
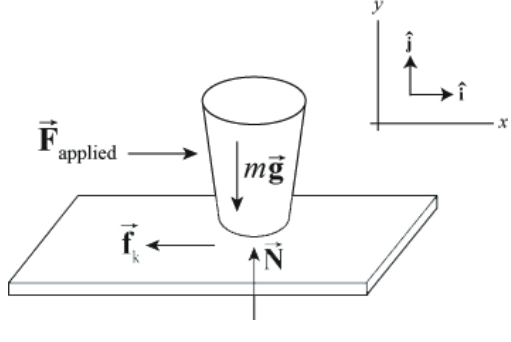
Let’s choose our coordinate system so that the +x -direction is the direction of the forward motion of the cup. The pushing force can then be described by
→Fa=Faxˆi
Suppose a body moves from an initial point xi to a final point xf so that the displacement of the point the force acts on is Δx≡xf−xi. The work done by a constant force →Fa=Faxˆi acting on the body is the product of the component of the force Fax and the displacement Δx ,
Wa=FaxΔx
Work is a scalar quantity; it is not a vector quantity. The SI unit for work is
[1N⋅m]=[1kg⋅m⋅s−2][1m]=[1kg⋅m2⋅s−2]=[1J]
Note that work has the same dimension and the same SI unit as kinetic energy. Because our applied force is along the direction of motion, both Fax>0 and Δx>0 In this example, the work done is just the product of the magnitude of the applied force and the distance through which that force acts and is positive. In the definition of work done by a force, the force can act at any point on the body. The displacement that appears in Equation (13.4.2) is not the displacement of the body but the displacement of the point of application of the force. For point-like objects, the displacement of the point of application of the force is equal to the displacement of the body. However for an extended body, we need to focus on where the force acts and whether or not that point of application undergoes any displacement in the direction of the force as the following example illustrates.
Example 13.2 Work Done by Static Fiction
Suppose you are initially standing and you start walking by pushing against the ground with your feet and your feet do not slip. What is the work done by the static friction force acting on you?
Solution: When you apply a contact force against the ground, the ground applies an equal and opposite contact force on you. The tangential component of this constant force is the force of static friction acting on you. Since your foot is at rest while you are pushing against the ground, there is no displacement of the point of application of this static friction force. Therefore static friction does zero work on you while you are accelerating. You may be surprised by this result but if you think about energy transformation, chemical energy stored in your muscle cells is being transformed into kinetic energy of motion and thermal energy.
When forces are opposing the motion, as in our example of pushing the cup, the kinetic friction force is given by
→Ff=fk,xˆi=−μkNˆi=−μkmgˆi
Here the component of the force is in the opposite direction as the displacement. The work done by the kinetic friction force is negative,
Wf=−μkmgΔx
Since the gravitation force is perpendicular to the motion of the cup, the gravitational force has no component along the line of motion. Therefore the gravitation force does zero work on the cup when the cup is slid forward in the horizontal direction. The normal force is also perpendicular to the motion, and hence does no work.
We see that the pushing force does positive work, the kinetic friction force does negative work, and the gravitation and normal force does zero work.
Example 13.3 Work Done by Force Applied in the Direction of Displacement
Push a cup of mass 0.2 kg along a horizontal table with a force of magnitude 2.0 N for a distance of 0.5 m. The coefficient of friction between the table and the cup is μk=0.10 Calculate the work done by the pushing force and the work done by the friction force.
Solution: The work done by the pushing force is
Wa=FaxΔx=(2.0N)(0.5m)=1.0J
The work done by the friction force is
Wf=−μkmgΔx=−(0.1)(0.2kg)(9.8m⋅s−2)(0.5m)=−0.10J
Example 13.4 Work Done by Force Applied at an Angle to the Direction of Displacement
Suppose we push the cup in the previous example with a force of the same magnitude but at an angle θ=30∘ upwards with respect to the table. Calculate the work done by the pushing force. Calculate the work done by the kinetic friction force.
Solution: The force diagram on the cup and coordinate system is shown in Figure 13.3.
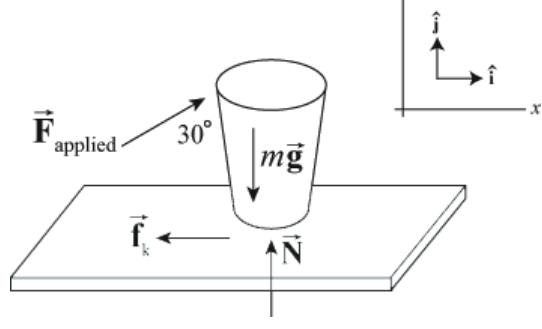
The x -component of the pushing force is now
Fax=Facos(θ)=(2.0N)(cos(30∘))=1.7N
The work done by the pushing force is
Wa=FaxΔx=(1.7N)(0.5m)=8.7×10−1J
The kinetic friction force is
→Ff=−μkNˆi
In this case, the magnitude of the normal force is not simply the same as the weight of the cup. We need to find the y -component of the applied force,
Fay=Fasin(θ)=(2.0N)(sin(30∘)=1.0N
To find the normal force, we apply Newton’s Second Law in the y -direction,
Fay+N−mg=0
Then the normal force is
N=mg−Fay=(0.2kg)(9.8m⋅s−2)−(1.0N)=9.6×10−1N
The work done by the kinetic friction force is
Wf=−μkNΔx=−(0.1)(9.6×10−1N)(0.5m)=4.8×10−2J
Example 13.5 Work done by Gravity Near the Surface of the Earth
Consider a point-like body of mass m near the surface of the earth falling directly towards the center of the earth. The gravitation force between the body and the earth is nearly constant, →Fgrav=m→g. Let’s choose a coordinate system with the origin at the surface of the earth and the + y -direction pointing away from the center of the earth Suppose the body starts from an initial point yi and falls to a final point yf closer to the earth. How much work does the gravitation force do on the body as it falls?
Solution: The displacement of the body is negative, Δy≡yf−yi<0. The gravitation force is given by
→Fg=m→g=Fgyˆj=−mgˆj
The work done on the body is then
Wg=FgyΔy=−mgΔy
For a falling body, the displacement of the body is negative, Δy≡yf−yi<0; therefore the work done by gravity is positive, Wg>0. The gravitation force is pointing in the same direction as the displacement of the falling object so the work should be positive.
When an object is rising while under the influence of a gravitation force, Δy≡yf−yi>0. The work done by the gravitation force for a rising body is negative, Wg<0, because the gravitation force is pointing in the opposite direction from that in which the object is displaced.
It’s important to note that the choice of the positive direction as being away from the center of the earth (“up”) does not make a difference. If the downward direction were chosen positive, the falling body would have a positive displacement and the gravitational force as given in Equation (13.4.15) would have a positive downward component; the product FgyΔy would still be positive.


