16.2: Fixed Axis Rotation- Rotational Kinematics
- Page ID
- 24523
Fixed Axis Rotation
A simple example of rotation about a fixed axis is the motion of a compact disc in a CD player, which is driven by a motor inside the player. In a simplified model of this motion, the motor produces angular acceleration, causing the disc to spin. As the disc is set in motion, resistive forces oppose the motion until the disc no longer has any angular acceleration, and the disc now spins at a constant angular velocity. Throughout this process, the CD rotates about an axis passing through the center of the disc, and is perpendicular to the plane of the disc (see Figure 16.1). This type of motion is called fixed-axis rotation.

When we ride a bicycle forward, the wheels rotate about an axis passing through the center of each wheel and perpendicular to the plane of the wheel (Figure 16.2). As long as the bicycle does not turn, this axis keeps pointing in the same direction. This motion is more complicated than our spinning CD because the wheel is both moving (translating) with some center of mass velocity, \(\overrightarrow{\mathbf{v}}_{\mathrm{cm}}\) and rotating with an angular speed \(\omega\).

When we turn the bicycle’s handlebars, we change the bike’s trajectory and the axis of rotation of each wheel changes direction. Other examples of non-fixed axis rotation are the motion of a spinning top, or a gyroscope, or even the change in the direction of the earth’s rotation axis. This type of motion is much harder to analyze, so we will restrict ourselves in this chapter to considering fixed axis rotation, with or without translation.
Angular Velocity and Angular Acceleration
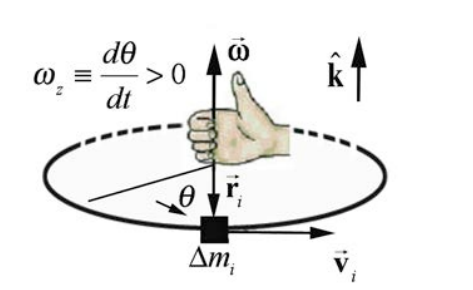
For a rigid body undergoing fixed-axis rotation, we can divide the body up into small volume elements with mass \(\Delta m_{i}\). Each of these volume elements is moving in a circle of radius \(r_{i}\) about the axis of rotation (Figure 16.3).

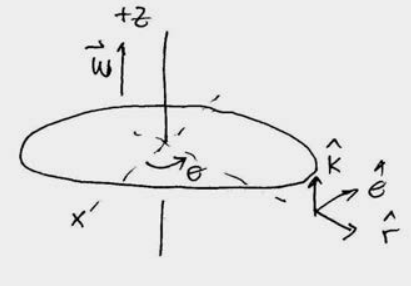
We will adopt the notation implied in Figure 16.3, and denote the vector from the axis to the point where the mass element is located as \(\overrightarrow{\mathbf{r}}_{i}\), with magnitude \(r_{i}=\left|\overrightarrow{\mathbf{r}}_{i}\right|\). Suppose the fixed axis of rotation is the z -axis. Introduce a right-handed coordinate system for an angle θ in the plane of rotation and the choice of the positive z -direction perpendicular to that plane of rotation. Recall our definition of the angular velocity vector. The angular velocity vector is directed along the z -axis with z -component equal to the time derivative of the angle θ,
\[\overrightarrow{\boldsymbol{\omega}}=\frac{d \theta}{d t} \hat{\mathbf{k}}=\omega_{z} \hat{\mathbf{k}} \nonumber \]
The angular velocity vector for the mass element undergoing fixed axis rotation with \(\omega_{z}>0\) is shown in Figure 16.4. Because the body is rigid, all the mass elements will have the same angular velocity \(\overrightarrow{\boldsymbol{\omega}}\) and hence the same angular acceleration \(\vec{\alpha}\). If the bodies did not have the same angular velocity, the mass elements would “catch up to” or “pass” each other, precluded by the rigid-body assumption.
In a similar fashion, all points in the rigid body have the same angular acceleration,
\[\vec{\alpha}=\frac{d^{2} \theta}{d t^{2}} \hat{\mathbf{k}}=\alpha_{z} \hat{\mathbf{k}} \nonumber \]
The angular acceleration vector is shown in Figure 16.5.

Sign Convention: Angular Velocity and Angular Acceleration
For rotational problems we shall always choose a right-handed cylindrical coordinate system. If the positive z -axis points up, then we choose θ to be increasing in the counterclockwise direction as shown in Figures 16.4 and 16.5. If the rigid body rotates in the counterclockwise direction, then the z -component of the angular velocity is positive, \(\omega_{z}=d \theta / d t>0\). The angular velocity vector then points in the \(+\hat{\mathbf{k}}\) -direction as shown in Figure 16.4. If the rigid body rotates in the clockwise direction, then the z -component of the angular velocity angular velocity is negative, \(\omega_{z}=d \theta / d t<0\). The angular velocity vector then points in the \(-\hat{\mathbf{k}}\)-direction.
If the rigid body increases its rate of rotation in the counterclockwise (positive) direction then the z -component of the angular acceleration is positive, \(\alpha_{z} \equiv d^{2} \theta / d t^{2}=d \omega_{z} / d t>0\). The angular acceleration vector then points in the \(+\hat{\mathbf{k}}\)-direction as shown in Figure 16.5. If the rigid body decreases its rate of rotation in the counterclockwise (positive) direction then the z -component of the angular acceleration is negative, \(\alpha_{z}=d^{2} \theta / d t^{2}=d \omega_{z} / d t<0\) The angular acceleration vector then points in the \(-\hat{\mathbf{k}}\)-direction. To phrase this more generally, if \(\vec{\alpha}\) and \(\overrightarrow{\boldsymbol{\omega}}\) point in the same direction, the body is speeding up, if in opposite directions, the body is slowing down. This general result is independent of the choice of positive direction of rotation. Note that in Figure 16.1, the CD has the angular velocity vector points downward (in the \(-\hat{\mathbf{k}}\)-direction.
Tangential Velocity and Tangential Acceleration
Because the small element of mass, \(\Delta m_{i}\) is moving in a circle of radius \(r_{i}\) with angular velocity \(\overrightarrow{\boldsymbol{\omega}}=\omega_{z} \hat{\mathbf{k}}\), the element has a tangential velocity component
\[v_{\theta, i}=r_{i} \omega_{z} \nonumber \]
If the magnitude of the tangential velocity is changing, the mass element undergoes a tangential acceleration given by
\[a_{\theta, i}=r_{i} \alpha_{z} \nonumber \]
Recall that the mass element is always accelerating inward with radial component given by
\[a_{r, i}=-\frac{v_{\theta, i}^{2}}{r_{i}}=-r_{i} \omega_{z}^{2} \nonumber \]
Example \(\PageIndex{1}\)
A turntable is a uniform disc of mass \(1.2\)kg and a radius \(1.3 \times 10^{1} \mathrm{cm}\). The turntable is spinning initially in a counterclockwise direction when seen from above at a constant rate of \(f_{0}=33 \text { cycles } \cdot \min ^{-1}\) (33 rpm ). The motor is turned off and the turntable slows to a stop in 8.0 s. Assume that the angular acceleration is constant. (a) What is the initial angular velocity of the turntable? (b) What is the angular acceleration of the turntable?
Solution
(a) Choose a coordinate system shown in Figure 16.6.
Initially, the disc is spinning with a frequency
\[f_{0}=\left(33 \frac{\text { cycles }}{\min }\right)\left(\frac{1 \min }{60 \mathrm{s}}\right)=0.55 \mathrm{cycles} \cdot \mathrm{s}^{-1}=0.55 \mathrm{Hz} \nonumber \]
so the initial angular velocity has magnitude
\[\omega_{0}=2 \pi f_{0}=\left(2 \pi \frac{\text { radian }}{\text { cycle }}\right)\left(0.55 \frac{\text { cycles }}{\mathrm{s}}\right)=3.5 \mathrm{rad} \cdot \mathrm{s}^{-1} \nonumber \]
The angular velocity vector points in the \(+\hat{\mathbf{k}}\)-direction as shown above.
(b) The final angular velocity is zero, so the component of the angular acceleration is
\[\alpha_{z}=\frac{\Delta \omega_{z}}{\Delta t}=\frac{\omega_{f}-\omega_{0}}{t_{f}-t_{0}}=\frac{-3.5 \mathrm{rad} \cdot \mathrm{s}^{-1}}{8.0 \mathrm{s}}=-4.3 \times 10^{-1} \mathrm{rad} \cdot \mathrm{s}^{-2} \nonumber \]
The z -component of the angular acceleration is negative, the disc is slowing down and so the angular acceleration vector then points in the \(-\hat{\mathbf{k}}\)-direction as shown in Figure 16.7.



