17.2: Vector Product (Cross Product)

Let $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ be two vectors. Because any two non-parallel vectors form a plane, we denote the angle θ to be the angle between the vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ as shown in Figure 17.2. The magnitude of the vector product $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ of the vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ is defined to be product of the magnitude of the vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ with the sine of the angle θ between the two vectors,

$$|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}| \sin (\theta) \nonumber$$

The angle θ between the vectors is limited to the values $0 \leq \theta \leq \pi$ ensuring that $\sin (\theta) \geq 0$.

Figure 17.2 Vector product geometry.

The direction of the vector product is defined as follows. The vectors $\overrightarrow{\mathbf{A}}$ and $\overrightarrow{\mathbf{B}}$ form a plane. Consider the direction perpendicular to this plane. There are two possibilities: we shall choose one of these two (the one shown in Figure 17.2) for the direction of the vector product $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ using a convention that is commonly called the “right-hand rule”.

Right-hand Rule for the Direction of Vector Product

The first step is to redraw the vectors $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$ so that the tails are touching. Then draw an arc starting from the vector $\overrightarrow{\mathbf{A}}$ and finishing on the vector $\overrightarrow{\mathbf{B}}$. Curl your right fingers the same way as the arc. Your right thumb points in the direction of the vector product $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ (Figure 17.3).

Figure 17.3 Right-Hand Rule.

You should remember that the direction of the vector product $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ is perpendicular to the plane formed by $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$. We can give a geometric interpretation to the magnitude of the vector product by writing the magnitude as

$$|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}|(|\overrightarrow{\mathbf{B}}| \sin \theta) \nonumber$$

The vectors $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$ form a parallelogram. The area of the parallelogram is equal to the height times the base, which is the magnitude of the vector product. In Figure 17.4, two different representations of the height and base of a parallelogram are illustrated. As depicted in Figure 17.4a, the term $|\overrightarrow{\mathbf{B}}| \sin \theta$ is the projection of the vector $\overrightarrow{\mathbf{B}}$ in the direction perpendicular to the vector $\overrightarrow{\mathbf{B}}$ We could also write the magnitude of the vector product as

$$|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=(|\overrightarrow{\mathbf{A}}| \sin \theta)|\overrightarrow{\mathbf{B}}| \nonumber$$

The term $|\overrightarrow{\mathbf{A}}| \sin \theta$ is the projection of the vector $\overrightarrow{\mathbf{A}}$ in the direction perpendicular to the vector $\overrightarrow{\mathbf{B}}$ as shown in Figure 17.4(b). The vector product of two vectors that are parallel (or anti-parallel) to each other is zero because the angle between the vectors is 0 (or $\pi$) and $\sin (0)=0$ (or $\sin (\pi)=0$). Geometrically, two parallel vectors do not have a unique component perpendicular to their common direction.

Figure 17.4 Projection of (a) $\overrightarrow{\mathbf{B}}$ perpendicular to $\overrightarrow{\mathbf{A}}$, (b) of $\overrightarrow{\mathbf{A}}$ perpendicular to $\overrightarrow{\mathbf{B}}$

Properties of the Vector Product

(1) The vector product is anti-commutative because changing the order of the vectors changes the direction of the vector product by the right hand rule:

$$\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{A}} \nonumber$$

(2) The vector product between a vector $c \overrightarrow{\mathbf{A}}$ where $c$ is a scalar and a vector $\overrightarrow{\mathbf{B}}$ is

$$c \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=c(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}) \nonumber$$

Similarly,

$$\overrightarrow{\mathbf{A}} \times c \overrightarrow{\mathbf{B}}=c(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}) \nonumber$$

(3) The vector product between the sum of two vectors $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$ with a vector $\overrightarrow{\mathbf{C}}$ is

$$(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}) \times \overrightarrow{\mathbf{C}}=\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}+\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}} \nonumber$$

Similarly,

$$\overrightarrow{\mathbf{A}} \times(\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}} \nonumber$$

Vector Decomposition and the Vector Product: Cartesian Coordinates

We first calculate that the magnitude of vector product of the unit vectors $\hat{\mathbf{i}}$ and $\hat{\mathbf{j}}$:

$$|\hat{\mathbf{i}} \times \hat{\mathbf{j}}|=|\hat{\mathbf{i}} \| \hat{\mathbf{j}}| \sin (\pi / 2)=1 \nonumber$$

because the unit vectors have magnitude $|\hat{\mathbf{i}}|=|\hat{\mathbf{j}}|=1$ and $\sin (\pi / 2)=1$. By the right hand rule, the direction of $\hat{\mathbf{i}} \times \hat{\mathbf{j}}$ is in the $+\hat{\mathbf{k}}$ as shown in Figure 17.5. Thus $\hat{\mathbf{i}} \times \hat{\mathbf{j}}=\hat{\mathbf{k}}$.

Figure 17.5 Vector product of $\hat{\mathbf{i}} \times \hat{\mathbf{j}}$

We note that the same rule applies for the unit vectors in the y and z directions,

$$\hat{\mathbf{j}} \times \hat{\mathbf{k}}=\hat{\mathbf{i}}, \quad \hat{\mathbf{k}} \times \hat{\mathbf{i}}=\hat{\mathbf{j}} \nonumber$$

By the anti-commutatively property (1) of the vector product,

$$\hat{\mathbf{j}} \times \hat{\mathbf{i}}=-\hat{\mathbf{k}}, \quad \hat{\mathbf{i}} \times \hat{\mathbf{k}}=-\hat{\mathbf{j}} \nonumber$$

The vector product of the unit vector $\hat{\mathbf{i}}$ with itself is zero because the two unit vectors are parallel to each other, $(\sin (0)=0)$,

$$|\hat{\mathbf{i}} \times \hat{\mathbf{i}}|=|\hat{\mathbf{i}}||\hat{\mathbf{i}}| \sin (0)=0 \nonumber$$

The vector product of the unit vector $\hat{\mathbf{j}}$ with itself and the unit vector $\hat{\mathbf{k}}$ with itself are also zero for the same reason,

$$|\hat{\mathbf{j}} \times \hat{\mathbf{j}}|=0, \quad|\hat{\mathbf{k}} \times \hat{\mathbf{k}}|=0 \nonumber$$

With these properties in mind we can now develop an algebraic expression for the vector product in terms of components. Let’s choose a Cartesian coordinate system with the vector $\overrightarrow{\mathbf{B}}$ pointing along the positive x-axis with positive x-component $B_{x}$. Then the vectors $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$ can be written as

$$\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}} \nonumber$$

$$\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}} \nonumber$$

respectively. The vector product in vector components is

$$\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left(A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}}\right) \times B_{x} \hat{\mathbf{i}} \nonumber$$

This becomes,

$$\begin{aligned} \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{x} \hat{\mathbf{i}} \times B_{x} \hat{\mathbf{i}}\right)+\left(A_{y} \hat{\mathbf{j}} \times B_{x} \hat{\mathbf{i}}\right)+\left(A_{z} \hat{\mathbf{k}} \times B_{x} \hat{\mathbf{i}}\right) \\ &=A_{x} B_{x}(\hat{\mathbf{i}} \times \hat{\mathbf{i}})+A_{y} B_{x}(\hat{\mathbf{j}} \times \hat{\mathbf{i}})+A_{z} B_{x}(\hat{\mathbf{k}} \times \hat{\mathbf{i}}) \\ &=-A_{y} B_{x} \hat{\mathbf{k}}+A_{z} B_{x} \hat{\mathbf{j}} \end{aligned} \nonumber$$

The vector component expression for the vector product easily generalizes for arbitrary vectors

$$\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}} \nonumber$$

$$\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_{z} \hat{\mathbf{k}} \nonumber$$

to yield

$$\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left(A_{y} B_{z}-A_{z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j}}+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \nonumber$$

Vector Decomposition and the Vector Product: Cylindrical Coordinates

Recall the cylindrical coordinate system, which we show in Figure 17.6. We have chosen two directions, radial and tangential in the plane, and a perpendicular direction to the plane.

Figure 17.6 Cylindrical coordinates

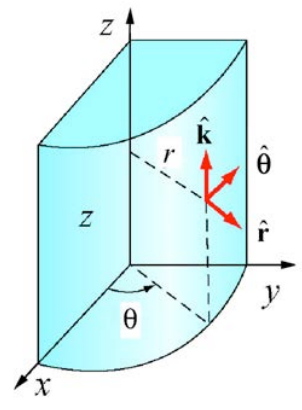
The unit vectors are at right angles to each other and so using the right hand rule, the vector product of the unit vectors are given by the relations

$$\hat{\mathbf{r}} \times \hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \nonumber$$

$$\hat{\boldsymbol{\theta}} \times \hat{\mathbf{k}}=\hat{\mathbf{r}} \nonumber$$

$$\hat{\mathbf{k}} \times \hat{\mathbf{r}}=\hat{\boldsymbol{\theta}} \nonumber$$

Because the vector product satisfies $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{A}}$ we also have that

$$\hat{\boldsymbol{\theta}} \times \hat{\mathbf{r}}=-\hat{\mathbf{k}} \nonumber$$

$$\hat{\mathbf{k}} \times \hat{\boldsymbol{\theta}}=-\hat{\mathbf{r}} \nonumber$$

$$\hat{\mathbf{r}} \times \hat{\mathbf{k}}=-\hat{\boldsymbol{\theta}} \nonumber$$

Finally

$$\hat{\mathbf{r}} \times \hat{\mathbf{r}}=\hat{\boldsymbol{\theta}} \times \hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \times \hat{\mathbf{k}}=\overrightarrow{\mathbf{0}} \nonumber$$

Example 17.1 Vector Products

Given two vectors, $\overrightarrow{\mathbf{A}}=2 \hat{\mathbf{i}}+-3 \hat{\mathbf{j}}+7 \hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{B}}=5 \hat{\mathbf{i}}+\hat{\mathbf{j}}+2 \hat{\mathbf{k}}$, find $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$.

Solution:

$$\begin{aligned} \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{y} B_{z}-A_{z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j}}+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \\ &=((-3)(2)-(7)(1)) \hat{\mathbf{i}}+((7)(5)-(2)(2)) \hat{\mathbf{j}}+((2)(1)-(-3)(5)) \hat{\mathbf{k}} \\ &=-13 \hat{\mathbf{i}}+31 \hat{\mathbf{j}}+17 \hat{\mathbf{k}} \end{aligned} \nonumber$$

Example 17.2 Law of Sines

For the triangle shown in Figure 17.7a, prove the law of sines, $|\overrightarrow{\mathbf{A}}| / \sin \alpha=|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin \gamma$, using the vector product.

Figure 17.7 (b) Vector analysis

Solution: Consider the area of a triangle formed by three vectors $\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf{B}}$, and $\overrightarrow{\mathbf{C}}$, where $\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}}=0$ (Figure 17.7b). Because $\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}}=0$, we have that $0=\overrightarrow{\mathbf{A}} \times(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}$. Thus $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}$ or $|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}|$. From Figure 17.7b we see that $|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}| \sin \gamma$ and $|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{C}}| \sin \beta$. Therefore $|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}| \sin \gamma=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{C}}| \sin \beta$, and hence $|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin \gamma$. A similar argument shows that $|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{A}}| / \sin \alpha$ proving the law of sines.

Example 17.3 Unit Normal

Find a unit vector perpendicular to $\overrightarrow{\mathbf{A}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{B}}=-2 \hat{\mathbf{i}}-\hat{\mathbf{j}}+3 \hat{\mathbf{k}}$.

Solution: The vector product $\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}$ is perpendicular to both $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$. Therefore the unit vectors $\hat{\mathbf{n}}=\pm \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} /|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|$ are perpendicular to both $\overrightarrow{\mathbf{A}} \text { and } \overrightarrow{\mathbf{B}}$. We first calculate

$$\begin{aligned} \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{y} B_{z}-A_{z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j}}+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \\ &=((1)(3)-(-1)(-1)) \hat{\mathbf{i}}+((-1)(2)-(1)(3)) \hat{\mathbf{j}}+((1)(-1)-(1)(2)) \hat{\mathbf{k}} \\ &=2 \hat{\mathbf{i}}-5 \hat{\mathbf{j}}-3 \hat{\mathbf{k}} \end{aligned} \nonumber$$

We now calculate the magnitude

$$|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=\left(2^{2}+5^{2}+3^{2}\right)^{1 / 2}=(38)^{1 / 2} \nonumber$$

Therefore the perpendicular unit vectors are

$$\hat{\mathbf{n}}=\pm \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} /|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=\pm(2 \hat{\mathbf{i}}-5 \hat{\mathbf{j}}-3 \hat{\mathbf{k}}) /(38)^{1 / 2} \nonumber$$

Example 17.4 Volume of Parallelepiped

Show that the volume of a parallelepiped with edges formed by the vectors $\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf{B}}, \text { and }$ $\overrightarrow{\mathbf{C}}$ is given by $\overrightarrow{\mathbf{A}} \cdot(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}})$.

Solution: The volume of a parallelepiped is given by area of the base times height. If the base is formed by the vectors $\overrightarrow{\mathbf{B}} \text { and } \overrightarrow{\mathbf{C}}$, then the area of the base is given by the magnitude of $\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}$. The vector $\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}=|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}| \hat{\mathbf{n}}$ where $\hat{\mathbf{n}}$ is a unit vector perpendicular to the base (Figure 17.8).

Figure 17.8 Example 17.4

The projection of the vector $\overrightarrow{\mathbf{A}}$ along the direction $\hat{\mathbf{n}}$ gives the height of the parallelepiped. This projection is given by taking the dot product of $\overrightarrow{\mathbf{A}}$ with a unit vector and is equal to $\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}=\text { height }$. Therefore

$$\overrightarrow{\mathbf{A}} \cdot(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \cdot(|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}|) \hat{\mathbf{n}}=(|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}|) \overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}=(\text { area })(\text { height })=(\text { volume }) \nonumber$$

Example 17.5 Vector Decomposition

Let $\overrightarrow{\mathbf{A}}$ be an arbitrary vector and let $\hat{\mathbf{n}}$ be a unit vector in some fixed direction. Show that $\overrightarrow{\mathbf{A}}=(\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}) \hat{\mathbf{n}}+(\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{n}}$

Solution: Let $\overrightarrow{\mathbf{A}}=A_{\|} \hat{\mathbf{n}}+A_{\perp} \hat{\mathbf{e}}$ where $A_{\|}$ is the component $\overrightarrow{\mathbf{A}}$ in the direction of $\hat{\mathbf{n}}, \hat{\mathbf{e}}$ is the direction of the projection of $\overrightarrow{\mathbf{A}}$ in a plane perpendicular to $\hat{\mathbf{n}}$, and $A_{\perp}$ is the component of $\overrightarrow{\mathbf{A}}$ in the direction of $\hat{\mathbf{e}}$. Because $\hat{\mathbf{e}} \cdot \hat{\mathbf{n}}=0$, we have that $\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}=A_{\|}$. Note that

$$\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}=\hat{\mathbf{n}} \times\left(A \hat{\mathbf{n}}+A_{\perp} \hat{\mathbf{e}}\right)=\hat{\mathbf{n}} \times A_{\perp} \hat{\mathbf{e}}=A_{\perp}(\hat{\mathbf{n}} \times \hat{\mathbf{e}}) \nonumber$$

The unit vector $\hat{\mathbf{n}} \times \hat{\mathbf{e}}$ lies in the plane perpendicular to $\hat{\mathbf{n}}$ and is also perpendicular to $\hat{\mathbf{e}}$. Therefore $(\hat{\mathbf{n}} \times \hat{\mathbf{e}}) \times \hat{\mathbf{n}}$ is also a unit vector that is parallel to $\hat{\mathbf{e}}$ (by the right hand rule. So $(\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{n}}=A_{\perp} \hat{\mathbf{e}}$. Thus

$$\overrightarrow{\mathbf{A}}=A_{\|} \hat{\mathbf{n}}+A_{\perp} \hat{\mathbf{e}}=(\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}) \hat{\mathbf{n}}+(\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{n}} \nonumber$$