29.4: Ideal Gas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider a gas consisting of a large number of molecules inside a rigid container. We shall assume that the volume occupied by the molecules is small compared to the volume occupied by the gas, that is, the volume of the container (dilute gas assumption). We also assume that the molecules move randomly and satisfy Newton’s Laws of Motion. The gas molecules collide with each other and the walls of the container. We shall assume that all the collisions are instantaneous and any energy converted to potential energy during the collision is recoverable as kinetic energy after the collision is finished. Thus the collisions are elastic and have the effect of altering the direction of the velocities of the molecules but not their speeds. We also assume that the intermolecular interactions contribute negligibly to the internal energy.
Internal Energy of a Monatomic Gas
An ideal monatomic gas atom has no internal structure, so we treat it as point particle. Therefore there are no possible rotational degrees of freedom or internal degrees of freedom; the ideal gas has only three degrees of freedom, and the internal energy of the ideal gas is Eintemal =N32kT Equation (29.4.1) is called the thermal equation of state of a monatomic ideal gas. The average kinetic energy of each ideal gas atom is then 12m(v2)ave=32kT where (v2)ave is the average of the square of the speeds and is given by (v2)ave=3kTm The temperature of this ideal gas is proportional to the average kinetic of the ideal gas molecule. It is an incorrect inference to say that temperature is defined as the mean kinetic energy of gas. At low temperatures or non-dilute densities, the kinetic energy is no longer proportional to the temperature. For some gases, the kinetic energy depends on number density and a more complicated dependence on temperature than that given in Equation (29.4.2).
Pressure of an Ideal Gas
Consider an ideal gas consisting of a large number N of identical gas molecules, each of mass m, inside a container of volume V and pressure P. The number of gas molecules per unit volume is then n=N/V. The density of the gas is ρ=nm. The gas molecules collide elastically with each other and the walls of the container. The pressure that the gas exerts on the container is due to the elastic collisions of the gas molecules with the walls of the container. We shall now use concepts of energy and momentum to model collisions between the gas molecules and the walls of the container in order to determine the pressure of the gas in terms of the volume V , particle number N and Kelvin temperature T
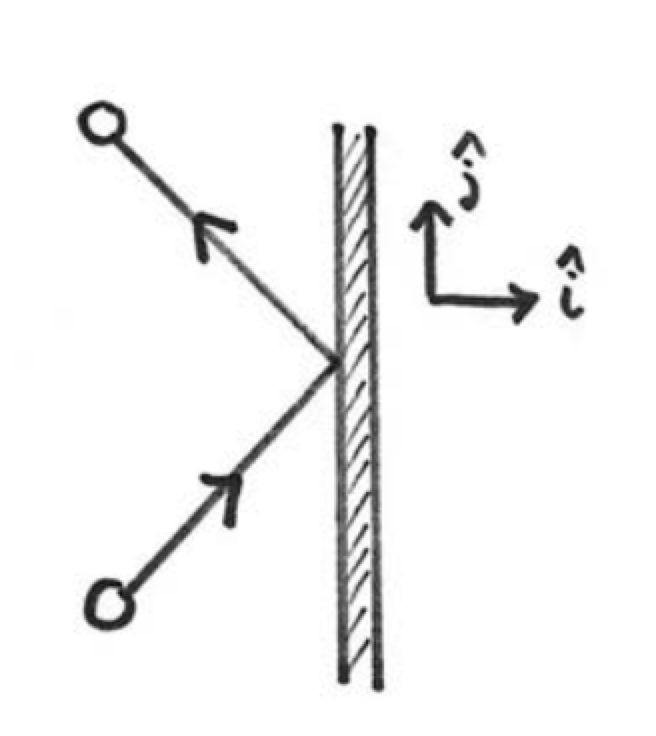
We begin by considering the collision of one molecule with one of the walls of the container, oriented with a unit normal vector pointing out of the container in the positive ˆi-direction (Figure 29.2). Suppose the molecule has mass m and is moving with velocity →v=vxˆi+vyˆj+vzˆk. Because the collision with the wall is elastic, the y -and z - components of the velocity of the molecule remain constant and the x-component of the velocity changes sign (Figure 29.2), resulting in a change of momentum of the gas molecule; Δ→pm=→pm,f−→pm,i=−2mvxˆi Therefore the momentum transferred by the gas molecule to the wall is Δ→pw=2mvxˆi Now, let’s consider the effect of the collisions of a large number of randomly moving molecules. For our purposes, “random” will be taken to mean that any direction of motion is possible, and the distribution of velocity components is the same for each direction.
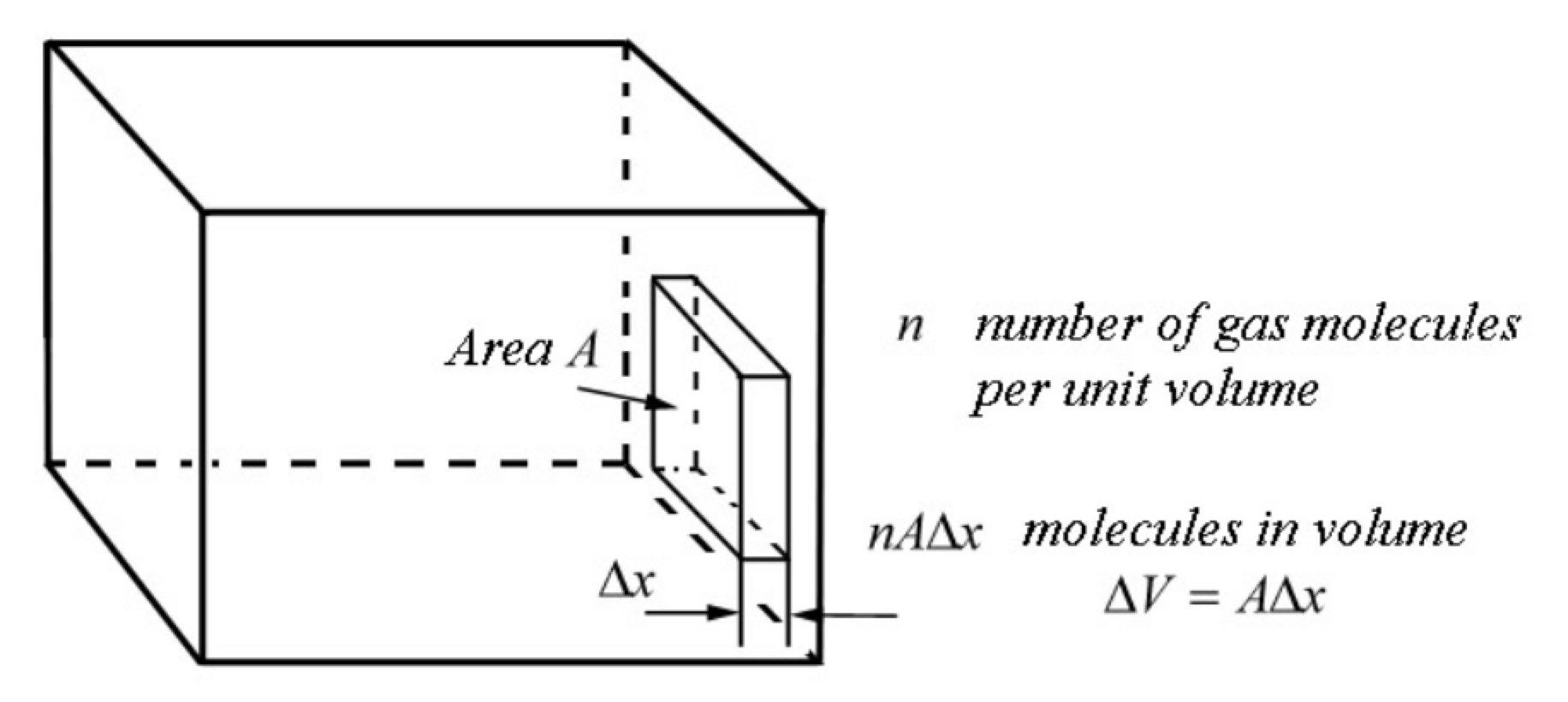
Consider a small rectangular volume ΔV=AΔx of gas adjacent to one of the walls of the container as shown in Figure 29.3. There are nAΔx gas molecules in this small volume. Let each group have the same x-component of the velocity. Let nj denote the number of gas molecules in the jth group with x -component of the velocity vx,j. Because the gas molecules are moving randomly, only half of the gas molecules in each group will be moving towards the wall in the positive x -direction. Therefore in a time interval Δtj=Δx/vx,j, the number of gas molecules that strike the wall with x-component of the velocity Vx,j is given by Δnj=12njAΔx (During this time interval some gas molecules may leave the edges of the box, but because the number that cross the area per second is proportional to the area, in the limit as Δx → 0, the number leaving the edges also approaches zero.) The number of gas molecules per second is then ΔnjΔtj=12njAΔxΔtj=12njAvx,j The momentum per second that the gas molecules in this group deliver to the wall is Δ→pjΔtj=ΔnjΔtj2mvx,jˆj=njmAv2x,jˆi By Newton’s Second Law, the average force on the wall due to this group of molecules is equal to the momentum per second delivered by the gas molecules to the wall; (→Fj,w)ave=Δ→pjΔtj=njmAv2x,jˆi The pressure contributed by this group of gas molecules is then Pj=|(→Fj,w)ave|A=njmv2x,j The pressure exerted by all the groups of gas molecules is the sum P=j=Ng∑j=1(Pj)ave =mj=Ng∑j=1njv2x,j The average of the square of the x -component of the velocity is given by (v2x)ave =1nj=Ng∑j=1njv2x,j where n is the number of gas molecules per unit volume in the container. Therefore we can rewrite Equation (29.4.11) as P=mn(v2x)ave =ρ(v2x)ave where ρ is the density of the gas. Because we assumed that the gas molecules are moving randomly, the average of the square of the x -, y - and z -components of the velocity of the gas molecules are equal, (v2x)ave =(v2y)ave =(v2z)ave The average of the square of the speed (v2)ave is equal to the sum of the average of the squares of the components of the velocity, (v2)ave =(v2x)ave +(v2y)ave +(v2z)ave . Therefore (v2)ave =3(v2x)ave Substituting Equation (29.4.16) into Equation (29.4.13) for the pressure of the gas yields P=13ρ(v2)ave
The square root of (v2)ave is called the root-mean-square (“rms”) speed of the molecules
Substituting Equation (29.4.3) into Equation (29.4.17) yields P=ρkTm Recall that the density of the gas ρ=MV=NmV Therefore Equation (29.4.18) can be rewritten as P=NkTV Equation (29.4.20) can be re-expressed as PV=NkT Equation (29.4.21) is known as the ideal gas equation of state also known as the Perfect Gas Law or Ideal Gas Law.
The total number of molecules in the gas N=nmNA where nm is the number of moles and NA is the Avogadro constant. The ideal gas law becomes PV=nmNAkT The universal gas constant is R=kNA=8.31J⋅K−1⋅mol−1. The ideal gas law can be re-expressed as PV=nmRT Although we started with atomistic description of the collisions of individual gas molecules satisfying the principles of conservation of energy and momentum, we ended up with a relationship between the macroscopic variables pressure, volume, number of moles, and temperature that are measurable properties of the system.
One important consequence of the Ideal Gas Law is that equal volumes of different ideal gases at the same temperature and pressure must contain the same number of molecules, N=1kPVT When gases combine in chemical reactions at constant temperature and pressure, the numbers of each type of gas molecule combine in simple integral proportions. This implies that the volumes of the gases must always be in simple integral proportions. Avogadro used this last observation about gas reactions to define one mole of a gas as a unit for large numbers of particles.

