1.7: Self-test Problems

Last updated
Save as PDF

Page ID: 34743

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

1.1. A bicycle, ridden with velocity \(v\) on a wet pavement, has no mudguards on its wheels. How far behind should the following biker ride to avoid being splashed over? Neglect the air resistance effects.

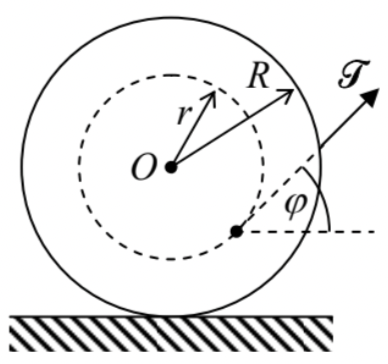
1.2. Two round disks of radius \(R\) are firmly connected with a coaxial cylinder of a smaller radius \(r\), and a thread is wound on the resulting spool. The spool is placed on a horizontal surface, and the thread’s end is being pooled out at angle \(\varphi\) - see the figure on the right. Assuming that the spool does not slip on the surface, what direction would it roll?

Screen Shot 2022-01-25 at 8.49.22 PM.png

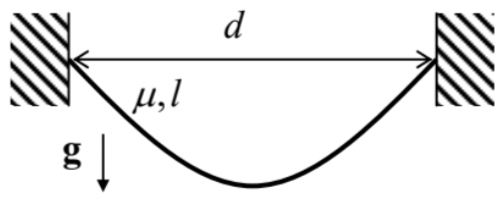
1.3.* Calculate the equilibrium shape of a flexible, heavy rope of length \(l\), with a constant mass \(\mu\) per unit length, if it is hung in a uniform gravity field between two points separated by a horizontal distance \(d\) - see the figure on the right.

Screen Shot 2022-01-25 at 8.53.11 PM.png

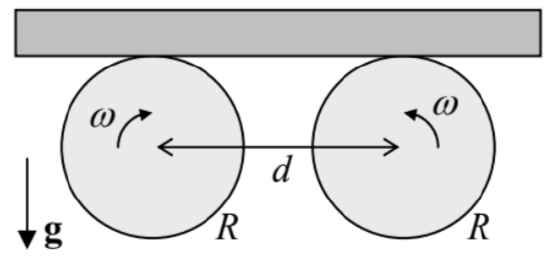
1.4. A uniform, long, thin bar is placed horizontally on two similar round cylinders rotating toward each other with the same angular velocity \(\omega\) and displaced by distance \(d-\) see the figure on the right. Calculate the laws of relatively slow horizontal motion of the bar within the plane of the drawing, for both possible directions of cylinder rotation, assuming that the friction force between the slipping surfaces of the bar and each cylinder obeys the simple Coulomb approximation \({ }^{26}|F|=\mu N\), where \(N\) is the normal pressure force between them, and \(\mu\) is a constant (velocity-independent) coefficient. Formulate the condition of validity of your result.

Screen Shot 2022-01-25 at 8.54.52 PM.png

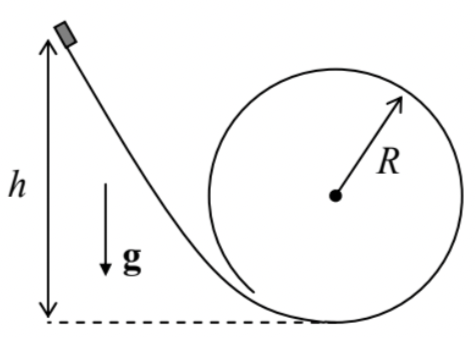
1.5. A small block slides, without friction, down a smooth slide that ends with a round loop of radius \(R\) - see the figure on the right. What smallest initial height \(h\) allows the block to make its way around the loop without dropping from the slide if it is launched with negligible initial velocity?

Screen Shot 2022-01-25 at 8.55.42 PM.png

1.6. A satellite of mass \(m\) is being launched from height \(H\) over the surface of a spherical planet with radius \(R\) and mass \(M \gg m-\) see the figure on the right. Find the range of initial velocities \(\mathbf{v}_{0}\) (normal to the radius) providing closed orbits above the planet’s surface.

Screen Shot 2022-01-25 at 8.58.30 PM.png

1.7. Prove that the thin-uniform-disk model of a galaxy describes small harmonic oscillations of stars inside it along the direction normal to the disk, and calculate the frequency of these oscillations in terms of Newton’s gravitational constant \(G\) and density \(\rho\) of the disk’s matter.

1.8. Derive differential equations of motion for small oscillations of two similar pendula coupled with a spring (see the figure on the right), within their common vertical plane. Assume that at the vertical position of both pendula, the spring is not stretched \((\Delta L=0)\).

Screen Shot 2022-01-25 at 8.59.09 PM.png

1.9. One of the popular futuristic concepts of travel is digging a straight railway tunnel through the Earth and letting a train go through it, without initial velocity - driven only by gravity. Calculate the train’s travel time through such a tunnel, assuming that the Earth’s density \(\rho\) is constant, and neglecting the friction and planet-rotation effects.

1.10. A small bead of mass \(m\) may slide, without friction, along a light string, stretched with a force \(\mathscr{T} \gg m g\), between two points separated by a horizontal distance \(2 d-\) see the figure on the right. Calculate the frequency of horizontal oscillations of the bead about its equilibrium position.

Screen Shot 2022-01-25 at 9.01.03 PM.png

1.11. For a rocket accelerating due to its working jet motor (and hence spending the jet fuel), calculate the relation between its velocity and the remaining mass.

Hint: For the sake of simplicity, consider the 1D motion.

1.12. Prove the following virial theorem: \({ }^{27}\) for a set of \(N\) particles performing a periodic motion, \[\bar{T}=-\frac{1}{2} \sum_{k=1}^{N} \overline{\mathbf{F}_{k} \cdot \mathbf{r}_{k}},\] where the top bar means averaging over time - in this case over the motion period. What does the virial theorem say about:

(i) a 1D motion of a particle in the confining potential28 \(U(x)=a x^{2 s}\), with \(a>0\) and \(s>0\), and

(ii) an orbital motion of a particle in the central potential \(U(r)=-C / r\) ?

Hint: Explore the time derivative of the following scalar function of time: \(G(t) \equiv \sum_{k=1}^{N} \mathbf{p}_{k} \cdot \mathbf{r}_{k}\).

\({ }^{26}\) It was suggested in 1785 by the same Charles-Augustin de Coulomb who has discovered the famous Coulomb law of electrostatics, and hence pioneered the whole quantitative science of electricity - see EM Ch. \(1 .\)

\({ }^{27}\) It was first stated by Rudolf Clausius in 1870 .

\({ }^{28}\) Here and below I am following the (regretful) custom of using the single word "potential" for the potential energy of the particle - just for brevity. This custom is also common in quantum mechanics, but in electrodynamics these two notions should be clearly distinguished - as they are in the EM part of this series.