4.7: Exercise Problems
- Page ID
- 34766
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)4.1. Calculate the principal moments of inertia for the following uniform rigid bodies:
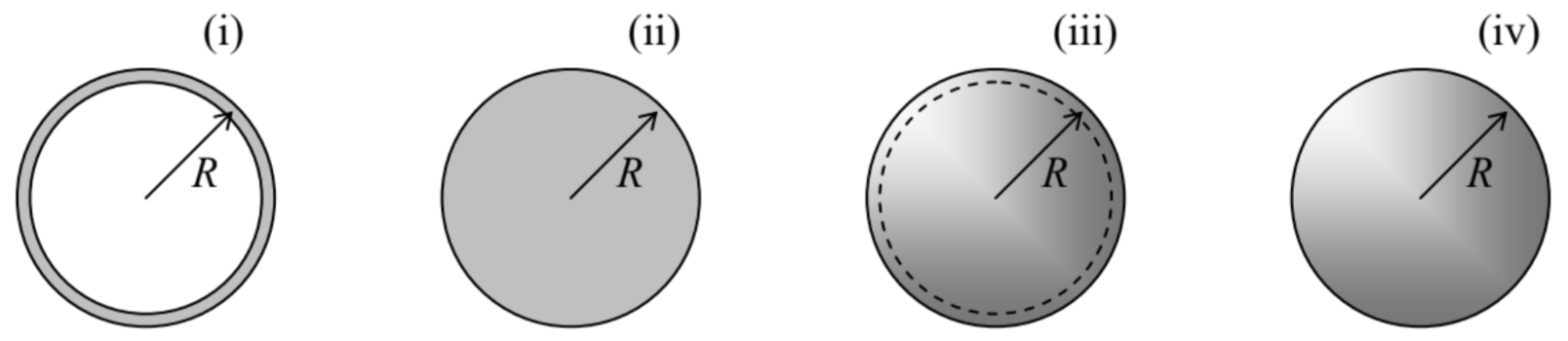
(i) a thin, planar, round hoop, (ii) a flat round disk, (iii) a thin spherical shell, and (iv) a solid sphere Compare the results, assuming that all the bodies have the same radius \(R\) and mass \(M\).
4.2. Calculate the principal moments of inertia for the rigid bodies shown in the figure below:
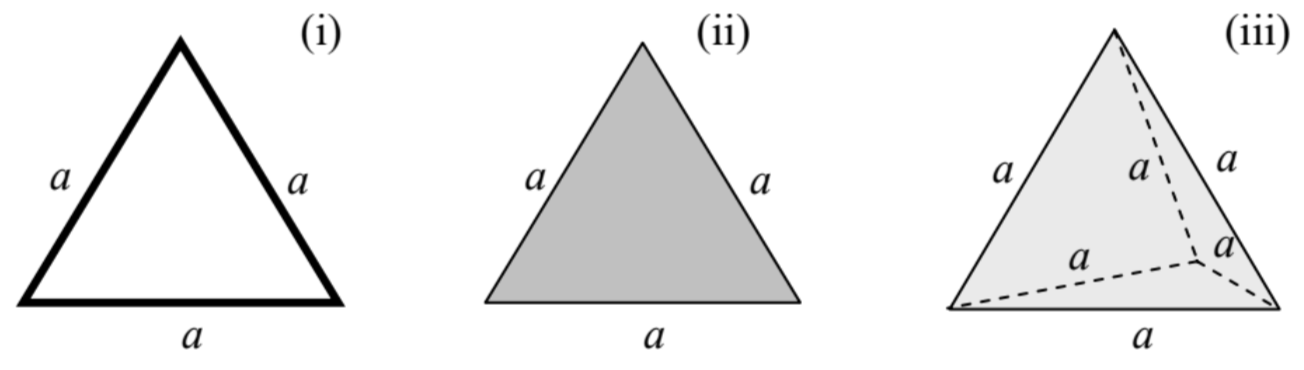
(i) an equilateral triangle made of thin rods with a uniform linear mass density \(\mu\),
(ii) a thin plate in the shape of an equilateral triangle, with a uniform areal mass density \(\sigma\), and
\({ }^{32}\) Note that by the definition (1.36), the angular momenta \(\mathbf{L}\) of particles merely add up. As a result, the final form of Eq. (102) is valid for an arbitrary system of particles. (iii) a tetrahedron made of a heavy material with a uniform bulk mass density \(\rho\).
Assuming that the total mass of the three bodies is the same, compare the results and give an interpretation of their difference.
4.3. Prove that Eqs. (34)-(36) are valid for rotation of a rigid body about a fixed axis \(z\), even if it does not pass through its center of mass.
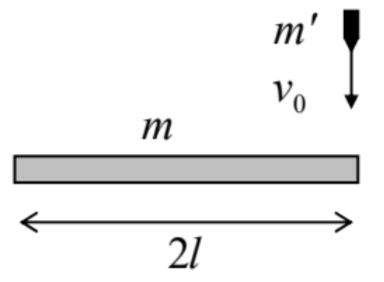
4.4. The end of a uniform thin rod of length \(2 l\) and mass \(m\), initially at rest, is hit by a bullet of mass \(m^{\prime}\), flying with velocity \(v_{0}\) (see the figure on the right), which gets stuck in the rod. Use two different approaches to calculate the velocity of the opposite end of the rod right after the collision.
4.5. A uniform ball is placed on a horizontal plane, while rotating with an angular velocity \(\omega_{0}\), but having no initial linear velocity. Calculate the angular velocity after the ball’s slippage stops, assuming the Coulomb approximation for the kinetic friction force: \(F_{f}=\mu N\), where \(N\) is a pressure between the surfaces, and \(\mu\) is a velocity-independent coefficient.
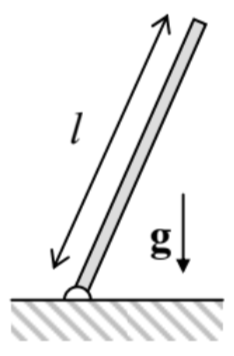
4.6. A body may rotate about a fixed horizontal axis \(\mathrm{A}-\) see Figure 5. Find the frequency of its small oscillations, in a uniform gravity field, as a function of the distance \(l\) of the axis from the body’s center of mass 0 , and analyze the result.
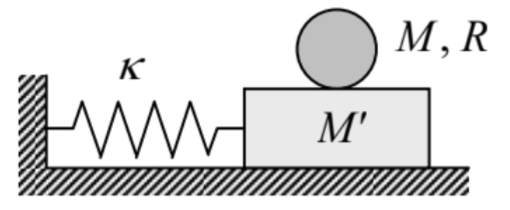
4.7. Calculate the frequency, and sketch the mode of oscillations of a round uniform cylinder of radius \(R\) and the mass \(M\), that may roll, without slipping, on a horizontal surface of a block of mass \(M\) ’. The block, in turn, may move in the same direction, without friction, on a horizontal surface, being connected to it with an elastic spring - see the figure on the right.
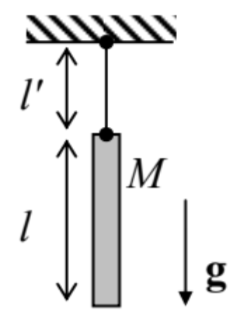
4.8. A thin uniform bar of mass \(M\) and length \(l\) is hung on a light thread of length \(l\) ’ (like a "chime" bell - see the figure on the right). Derive the equations of motion of the system within the plane of the drawing.
4.9. A solid, uniform, round cylinder of mass \(M\) can roll, without slipping, over a concave, round cylindrical surface of a block of mass \(M^{\prime}\), in a uniform gravity field - see the figure on the right. The block can slide without friction on a horizontal surface. Using the Lagrangian formalism,
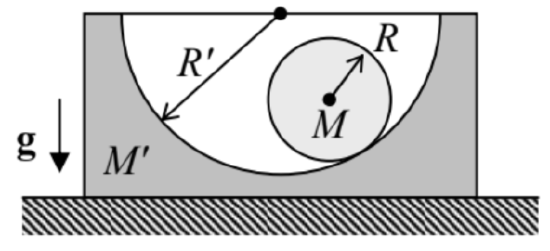
(i) find the frequency of small oscillations of the system near the equilibrium, and
(ii) sketch the oscillation mode for the particular case \(M^{\prime}=M, R^{\prime}=2 R\).
4.10. A uniform solid hemisphere of radius \(R\) is placed on a horizontal plane \(-\) see the figure on the right. Find the frequency of its small oscillations within a vertical plane, for two ultimate cases:
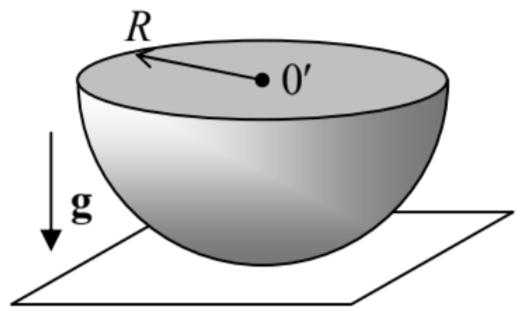
(i) there is no friction between the hemisphere and plane surfaces, and
(ii) the static friction is so strong that there is no slippage between these surfaces.
4.11. For the "sliding ladder" problem, started in Sec. 3 (see Figure 7), find the critical value \(\alpha_{\mathrm{c}}\) of the angle \(\alpha\) at that the ladder loses its contact with the vertical wall, assuming that it starts sliding from the vertical position, with a negligible initial velocity.
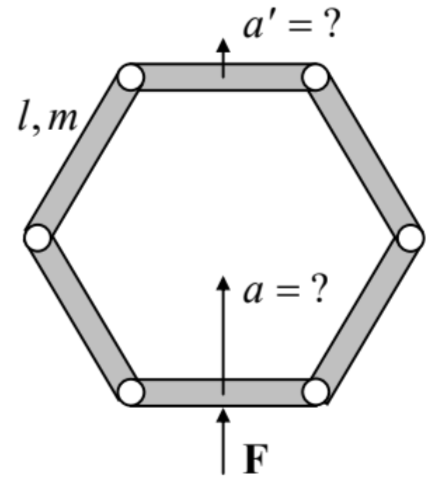
4.12. Six similar, uniform rods of length \(l\) and mass \(m\) are connected by light joints so that they may rotate, without friction, versus each other, forming a planar polygon. Initially, the polygon was at rest, and had the correct hexagon shape \(-\) see the figure on the right. Suddenly, an external force \(\mathbf{F}\) is applied to the middle of one rod, in the direction of the hexagon’s symmetry center. Calculate the accelerations: of the rod to which the force is applied \((a)\), and of the opposite rod \(\left(a^{\prime}\right)\), immediately after the application of the force.
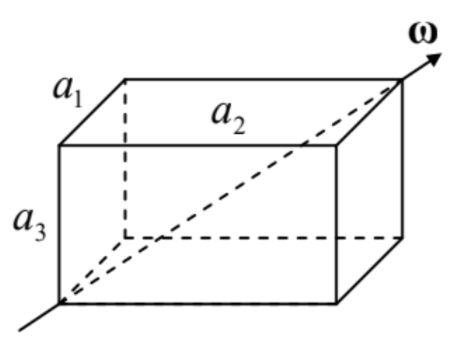
4.13. A rectangular cuboid (parallelepiped) with sides \(a_{1}, a_{2}\), and \(a_{3}\), made of a material with a constant mass density \(\rho\), is rotated, with a constant angular velocity \(\omega\), about one of its space diagonals - see the figure on the right. Calculate the torque \(\tau\) necessary to sustain such rotation.
4.14. One end of a light shaft of length \(l\) is firmly attached to the center of a thin uniform solid disk of radius \(R<<\) \(l\) and mass \(M\), whose plane is perpendicular to the shaft. Another end of the shaft is attached to a vertical axis (see the figure on the right) so that the shaft may rotate about the axis without friction. The disk rolls, without slippage, over a horizontal surface, so that the whole system rotates about the vertical axis with a constant angular velocity \(\omega\). Calculate the (vertical) supporting force \(N\) exerted on the disk by the surface.
4.15. An air-filled balloon is placed inside a water-filled container, which moves by inertia in free space, at negligible gravity. Suddenly, force \(\mathbf{F}\) is applied to the container, pointing in a certain direction. What direction does the balloon move relative to the container?
4.16. Two planets are in a circular orbit around their common center of mass. Calculate the effective potential energy of a much lighter body (say, a spacecraft) rotating with the same angular velocity, on the line connecting the planets. Sketch the plot of the radial dependence of \(U_{\text {ef }}\) and find out the number of so-called Lagrange points is which the potential energy has local maxima. Calculate their position explicitly in the limit when one of the planets is much more massive than the other one.
4.17. A small body is dropped down to the surface of Earth from height \(h<R_{\mathrm{E}}\), without initial velocity. Calculate the magnitude and direction of its deviation from the vertical, due to the Earth rotation. Estimate the effect’s magnitude for a body dropped from the Empire State Building. 4.18. Calculate the height of solar tides on a large ocean, using the following simplifying assumptions: the tide period ( \(1 / 2\) of Earth’s day) is much longer than the period of all ocean waves, the Earth (of mass \(M_{\mathrm{E}}\) ) is a sphere of radius \(R_{\mathrm{E}}\), and its distance \(r_{\mathrm{S}}\) from the Sun (of mass \(M_{\mathrm{S}}\) ) is constant and much larger than \(R_{\mathrm{E}}\).
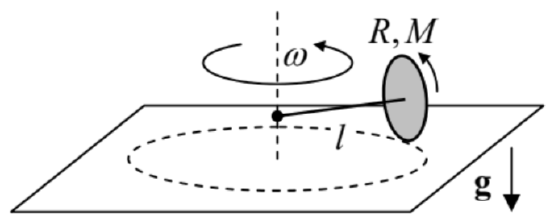
4.19. A coin of radius \(r\) is rolled, with velocity \(V\), on a horizontal surface without slippage. What should be the coin’s tilt angle \(\theta\) (see the figure on the right) for it to roll on a circle of radius \(R \gg>r\) ? Modeling the coin as a very thin, uniform disk, and assuming that the angle \(\theta\) is small, solve this problem in:
(i) an inertial ("lab") reference frame, and
(ii) the non-inertial reference frame moving with the coin’s center (but not rotating with it).
4.20. A satellite is on a circular orbit of radius \(R\), around the Earth.
(i) Write the equations of motion of a small body as observed from the satellite, and simplify them for the case when the motion is limited to the satellite’s close vicinity.
(ii) Use the equations to prove that the body may be placed on an elliptical trajectory around the satellite’s center of mass, within its plane of rotation about Earth. Calculate the ellipse’s orientation and eccentricity.
4.21. A non-spherical shape of an artificial satellite may ensure its stable angular orientation relative to Earth’s surface, advantageous for many practical goals. Modeling the satellite as a strongly elongated, axially-symmetric body, moving around the Earth on a circular orbit of radius \(R\), find its stable orientation.
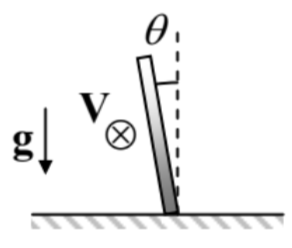
4.22. \({ }^{*}\) A rigid, straight, uniform rod of length \(l\), with the lower end on a pivot, falls in a uniform gravity field - see the figure on the right. Neglecting friction, calculate the distribution of the bending torque \(\tau\) along its length, and analyze the result.
Hint: The bending torque is the net torque of the force \(\mathbf{F}\) acting between two parts of the rod, mentally separated by its cross-section, about a certain "neutral axis". \({ }^{33}\) As will be discussed in detail in Sec. 7.5, at the proper definition of this axis, the bending torque’s gradient along the rod’s length is equal to \((-F)\), where \(F\) is the rod-normal ("shear") component of the force exerted by the top part of the rod on its lower part.
4.23. Let \(\mathbf{r}\) be the radius vector of a particle, as measured in a possibly non-inertial but certainly non-rotating reference frame. Taking its Cartesian components for the generalized coordinates, calculate the corresponding generalized momentum \(\boldsymbol{\mu}\) of the particle, and its Hamiltonian function \(H\). Compare \(\boldsymbol{\mu}\) with \(m \mathbf{v}\), and \(H\) with the particle’s energy \(E\). Derive the Lagrangian equation of motion in this approach, and compare it with Eq. (92).
\({ }^{34}\) Inadequate definitions of this torque are the main reason for numerous wrong solutions of this problem, posted online - readers beware!


