6.7: Nonlinear and Parametric Effects
- Page ID
- 34783
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now let me discuss (because of the lack of time, very briefly, on a semi-quantitative level), the new nonlinear and parametric phenomena that appear in oscillatory systems with more than one degree of freedom - cf. Secs. 5.4-5.8. One important new effect here is the mutual phase locking of (two or more) weakly coupled self-excited oscillators with close frequencies: if the own frequencies of the oscillators are sufficiently close, their oscillation frequencies "stick together" to become exactly equal. Though its dynamics of this process is very close to that of the phase locking of a single oscillator by an external signal, which was discussed in Sec. 5.4, it is rather counter-intuitive in the view of the results of Sec. 1, and in particular, the anticrossing diagram shown in Figure 2. The analysis of the effect using the van der Pol method (which is highly recommended to the reader, see Problem 16) shows that the origin of the difference is the oscillators’ nonlinearity, which makes oscillation amplitudes virtually independent of the phase evolution - see Eq. (5.68) and its discussion.
One more new effect is the so-called non-degenerate parametric excitation. It may be illustrated on the example of just two coupled oscillators - see Sec. 1 above. Let us assume that the coupling constant \(\kappa\), participating in Eqs. (5), is not constant, but oscillates in time - say with some frequency \(\omega_{\mathrm{p}}\). In this case, the forces acting on each oscillator from its counterpart, described by the right-hand side of Eqs. (5), will be proportional to \(\kappa q_{2,1}\left(1+\mu \cos \omega_{p} t\right)\). Assuming that the oscillations of \(q_{1}\) and \(q_{2}\) are close to sinusoidal ones, with certain frequencies \(\omega_{1,2}\), we see that the force exerted on each oscillator will contain the so-called combinational frequencies \[\omega_{\mathrm{p}} \pm \omega_{2,1}\] If one of these frequencies is close to the own oscillation frequency of the oscillator, we can expect a substantial parametric interaction between the oscillators (on top of the constant coupling effects discussed in Sec. 1). According to Eq. (89), this may happen in two cases: \[\begin{aligned} \omega_{\mathrm{p}} &=\omega_{1}+\omega_{2}, \\ \omega_{\mathrm{p}} &=\omega_{1}-\omega_{2} . \end{aligned}\] The quantitative analysis (also highly recommended to the reader, see Problem 18) shows that in the case (90a), the parameter modulation indeed leads to energy "pumping" into the oscillations. As a result, a sufficiently large \(\mu\), at sufficiently small damping coefficients \(\delta_{1,2}\) and the effective detuning \[\xi \equiv \omega_{\mathrm{p}}-\left(\Omega_{1}+\Omega_{2}\right),\] may lead to a simultaneous self-excitation of two frequency components \(\omega_{1,2}\). These frequencies, while being approximately equal to the corresponding own frequencies \(\Omega_{1,2}\) of the system, are related to the pumping frequency \(\omega_{\mathrm{p}}\) by the exact relation (90a), but otherwise are arbitrary, e.g., may be incommensurate (Figure 12a), thus justifying the term non-degenerate parametric excitation. \({ }^{27}\) (The parametric excitation of a single oscillator, that was analyzed in Sec. 5.5, is a particular, degenerate case of such excitation, with \(\omega_{1}=\omega_{2}=\omega_{\mathrm{p}} / 2\).) On the other hand, for the case described by Eq. (90b), the parameter modulation always pumps energy from the oscillations, effectively increasing the system’s damping.
Somewhat counter-intuitively, this difference between two cases (90) may be simpler interpreted using the basic notions of quantum mechanics. Namely, the equality \(\omega_{\mathrm{p}}=\omega_{1}+\omega_{2}\) enables a decay of an external photon of energy \(\hbar \omega_{0}\) into two photons of energies \(\hbar \omega_{1}\) and \(\hbar \omega_{2}\) of the oscillators. (On the contrary, the complementary relation (90b), meaning that \(\omega_{1}=\omega_{\mathrm{p}}+\omega_{2}\), results in a pumping-induced decay of photons of frequency \(\omega_{1}\).)
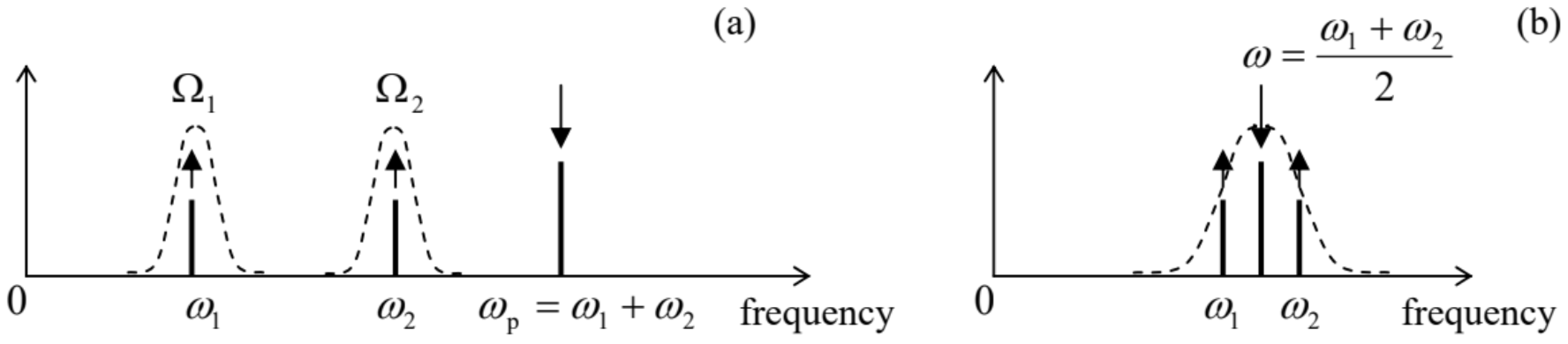 Figure 6.12. Spectra of oscillations at (a) the non-degenerate parametric excitation, and (b) the fourwave mixing. The arrow directions symbolize the energy flows into and out of the system.
Figure 6.12. Spectra of oscillations at (a) the non-degenerate parametric excitation, and (b) the fourwave mixing. The arrow directions symbolize the energy flows into and out of the system.Note that even if the frequencies \(\omega_{1}\) and \(\omega_{2}\) of the parametrically excited oscillations are incommensurate, the oscillations are highly correlated. Indeed, the quantum mechanical theory of this effect \({ }^{28}\) shows that the generated photons are entangled. This fact makes the parametric excitation very popular for a broad class of experiments in several currently active fields including quantum computation and encryption, and the Bell inequality/local reality studies. \({ }^{29}\)
Proceeding to nonlinear phenomena, let us note, first of all, that the simple reasoning that accompanied Eq. (5.108) in Sec. 5.8, is also valid in the case when oscillations consist of two (or more) sinusoidal components with incommensurate frequencies. Replacing the notation \(2 \omega\) with \(\omega_{\mathrm{p}}\), we see that the non-degenerate parametric excitation of the type (90a) is possible in a system of two coupled oscillators with a quadratic nonlinearity (of the type \(\gamma q^{2}\) ), "pumped" by an intensive external signal at frequency \(\omega_{\mathrm{p}} \approx \Omega_{1}+\Omega_{2}\). In optics, it is often more convenient to have all signals within the same, relatively narrow frequency range. A simple calculation, similar to the one made in Eqs. (5.107)-(5.108), shows that this may be done using the cubic nonlinearity \({ }^{30}\) of the type \(\alpha q^{3}\), which allows a similar parametric energy exchange at the frequency relation shown in Figure 12b: \[2 \omega=\omega_{1}+\omega_{2}, \quad \text { with } \omega \approx \omega_{1} \approx \omega_{2} .\] This process is often called the four-wave mixing, because it may be interpreted quantummechanically as the transformation of \(t w o\) externally-delivered photons, each with energy \(\hbar \omega\), into two other photons of energies \(\hbar \omega_{1}\) and \(\hbar \omega_{2}\). The word "wave" in this term stems from the fact that at optical frequencies, it is hard to couple a sufficient volume of a nonlinear medium with lumped-type resonators. It is much easier to implement the parametric excitation (as well as other nonlinear phenomena such as the higher harmonic generation) of light in distributed systems of a linear size much larger than the involved wavelengths. In such systems, the energy transfer from the incoming wave of frequency \(\omega\) to generated waves of frequencies \(\omega_{1}\) and \(\omega_{2}\) is gradually accumulated at their joint propagation along the system. From the analogy between Eq. (85) (describing the evolution of the wave’s amplitude in space), and the usual equation of the linear oscillator (describing its evolution in time), it is clear that this energy transfer accumulation requires not only the frequencies \(\omega\), but also the wave numbers \(k\) be in similar relations. For example, the four-wave mixing requires that not only the frequency balance (92a), but also a similar relation \[2 k=k_{1}+k_{2},\] to be fulfilled. Since all three frequencies are close, this relation is easy to arrange. Unfortunately, due to the lack of time/space, for more discussion of this very interesting subject, called nonlinear optics, I have to refer the reader to special literature. \({ }^{31}\)
It may look like a dispersion-free media, with \(\omega / k=v=\) const, is the perfect solution for arranging the parametric interaction of waves, because in such media, for example, Eq. (92b) automatically follows from Eq. (92a). However, in such a media not only the desirable three parametrically interacting waves but also all their harmonics, have the same velocity. At these conditions, the energy transfer rates between all harmonics are of the same order. Perhaps the most important result of such a multi-harmonic interaction is that intensive incident traveling waves, interacting with a nonlinear medium, may develop sharply non-sinusoidal waveforms, in particular those with an almost instant change of the field at a certain moment. Such shock waves, especially those of mechanical nature, are of large interest for certain applications - some of them not quite innocent, e.g., the dynamics of explosion in the usual (chemical) and nuclear bombs. \({ }^{32}\)
To conclude this chapter, let me note that the above discussion of 1D acoustic waves will be extended, in Sec. 7.7, to elastic 3D media. There we will see that generally, the waves obey a more complex equation than the apparently natural generalization of Eq. (40): \[\left(\frac{1}{v^{2}} \frac{\partial^{2}}{\partial t^{2}}-\nabla^{2}\right) q(\mathbf{r}, t)=0,\] where \(\nabla^{2}\) is the Laplace operator. This fact adds to the complexity of traveling-wave and standing-wave phenomena in higher dimensions. Moreover, in multi-dimensional systems, including such pseudo-1D systems as thin rods and pseudo-2D systems such as thin membranes, even static elastic deformations may be very nontrivial. A brief introduction to the general theory of small deformations, with a focus on elastic continua, will be the subject of the next chapter.
\({ }^{27}\) Note that in some publications, the term parametric down-conversion (PDC) is used instead.
\({ }^{28}\) Which is, surprisingly, not much more complex than the classical theory - see, e.g., QM Sec.5.5
\({ }^{29}\) See, e.g., QM Secs. \(8.5\) and \(10.3\), respectively.
\({ }^{30}\) In optics, such nonlinearity is implemented using transparent crystals such as lithium niobate \(\left(\mathrm{LiNbO}_{3}\right)\), with the cubic-nonlinear dependence of the electric polarization on the applied electric field: \(\mathscr{P} \propto \mathscr{E}+\alpha \mathscr{E}^{3}\).
\({ }^{31}\) See, e.g., N. Bloembergen, Nonlinear Optics, \(4^{\text {th }}\) ed., World Scientific, 1996, or a more modern treatment by R. Boyd, Nonlinear Optics, \(3^{\text {rd }}\) ed., Academic Press, 2008. This field is currently very active. As just a single example, let me mention the recent experiments with parametric amplification of ultrashort ( 20 -fs) optical pulses to peak power as high as \(\sim 5 \times 10^{12} \mathrm{~W}-\) see \(\mathrm{X}\). Zeng et al., Optics Lett. 42, 2014 (2017).
\({ }^{32}\) The classical (and perhaps still the best) monograph on the subject is Ya. Zeldovich, Physics of Shock Waves and High-Temperature Phenomena, Dover, \(2002 .\)


