8.2: Surface Tension Effects

Besides the bulk (volume-distributed) forces, one more possible source of pressure is surface tension. This effect results from the difference between the potential energy of atomic interactions on the interface between two different fluids and that in their bulks, and thus may be described by an additional potential energy \[U_{\mathrm{i}}=\gamma A,\] where \(A\) is the interface area, and \(\gamma\) is called the surface tension constant - or just the "surface tension". For a stable interface of any two fluids, \(\gamma\) is always positive. \({ }^{8}\) For surfaces of typical liquids (or their interfaces with air), at room temperature, the surface tension equals a few \(10^{-2} \mathrm{~J} / \mathrm{m}^{2}\), corresponding to the potential energy \(U_{\mathrm{i}}\) of a few \(10^{-2} \mathrm{eV}\) per surface molecule - i.e. just a fraction of the full binding (or "cohesive") energy of the same liquid, which is typically of the order of \(10^{-1} \mathrm{eV}\) per molecule.

In the absence of other forces, the surface tension makes a liquid drop spherical to minimize its surface area \(A\) at a fixed volume. For the analysis of the surface tension effects for more complex geometries, and in the presence of other forces, it is convenient to reduce it to a certain additional effective pressure drop \(\Delta \mathcal{P}_{\text {ef }}\) at the interface. To calculate \(\Delta \mathcal{P}_{\text {ef }}\), let us consider the condition of equilibrium of a small part \(d A\) of a smooth interface between two fluids (Figure 2), in the absence of bulk forces.

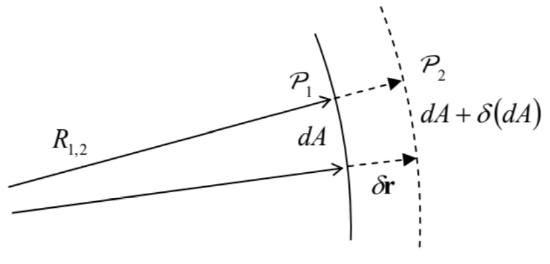Figure 8.4. Deriving the Young-Laplace formula (13).

If the pressures \(\mathcal{P}_{1,2}\) on the two sides of the interface are different, the work of stress forces on fluid 1 at a small virtual displacement \(\delta \mathbf{r}=\mathbf{n} \delta r\) of the interface (where \(\mathbf{n}=d \mathbf{A} / d A\) is the unit vector normal to the interface) equals \[\delta \mathscr{H}=d A \delta r\left(\mathcal{P}_{1}-\mathcal{P}_{2}\right) .\] For equilibrium, this work has to be compensated by an equal change of the interface energy, \(\delta U_{\mathrm{i}}=\) \(\gamma \delta(d A)\). Differential geometry tells us that in the linear approximation in \(\delta r\), the relative change of the elementary surface area, corresponding to a fixed solid angle \(d \Omega\), may be expressed as \[\frac{\delta(d A)}{d A}=\frac{\delta r}{R_{1}}+\frac{\delta r}{R_{2}},\] where \(R_{1,2}\) are the so-called principal radii of the interface curvature. \({ }^{10}\) Combining Eqs. (10)-(12), we get the Young-Laplace formula 11 \[\mathcal{P}_{1}-\mathcal{P}_{2}=\Delta \mathcal{P}_{\text {ef }} \equiv \gamma\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right) .\] In particular, this formula shows that the additional pressure created by surface tension inside a spherical drop of a liquid, of radius \(R\), equals \(2 \gamma / R\), i.e. decreases with \(R\). In contrast, according to Eqs. (5)-(6), the effects of bulk forces, for example gravity, grow as \(\rho g R\). The comparison of these two pressure components shows that if the drop radius (or more generally, the characteristic linear size of a fluid sample) is much larger than the so-called capillary length \[a_{\mathrm{c}} \equiv\left(\frac{2 \gamma}{\rho g}\right)^{1 / 2}\] the surface tension may be safely ignored - as will be done in all following sections of this chapter, besides a brief discussion at the end of Sec. 4. For the water surface, or more exactly its interface with air at ambient conditions, \(\gamma \approx 0.073 \mathrm{~J} / \mathrm{m}^{2}\) (i.e. \(\mathrm{N} / \mathrm{m}\) ), while \(\rho \approx 1,000 \mathrm{~kg} / \mathrm{m}^{3}\), so that \(a_{\mathrm{c}} \approx 4 \mathrm{~mm}\).

On the other hand, in very narrow tubes, such as blood capillary vessels with radius \(a \sim 1 \mu \mathrm{m}\), i.e. \(a<<a_{\mathrm{c}}\), the surface tension effects are very important. The key notion for the analysis of these effects is the contact angle \(\theta_{\mathrm{c}}\) (also called the "wetting angle") at an equilibrium edge of a liquid wetting a solid - see Figure 5 .

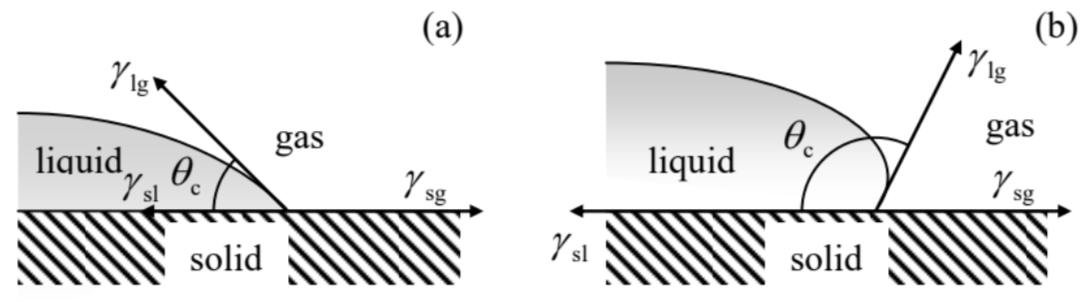Figure 8.5. Contact angles for (a) hydrophilic and (b) hydrophobic surfaces.

According to its definition (10), the constant \(\gamma\) may be interpreted as a force (per unit length of the interface boundary) directed normally to the boundary, and "trying" to reduce the interface area. As a result, the balance of horizontal components of the three such forces, shown in Figure 5a, immediately yields the Young’s equation \[\gamma_{\mathrm{sl}}+\gamma_{\mathrm{lg}} \cos \theta_{\mathrm{c}}=\gamma_{\mathrm{sg}},\] where the indices of constants \(\gamma\) correspond to three possible interfaces between the liquid, solid, and gas. For the so-called hydrophilic surfaces that "like to be wet" by a particular liquid (not necessarily water), meaning that \(\gamma_{\mathrm{sl}}<\gamma_{\mathrm{sg}}\), this relation yields \(\cos \theta_{\mathrm{c}}>0\), i.e. \(\theta_{\mathrm{c}}<\pi / 2-\) the situation shown in Figure 5a. On the other hand, for hydrophobic surfaces with \(\gamma_{\mathrm{sl}}>\gamma_{\mathrm{sg}}\), Eq. (15) yields larger contact angles, \(\theta_{\mathrm{c}}>\pi / 2\) - see Figure \(5 b\).

Let us use this notion to solve the simplest and perhaps the most practically important problem of this field - find the height \(h\) of the fluid column lifted by the surface tension forces in a narrow vertical tube made of a hydrophilic material, assuming its internal surface to be a round cylinder of radius \(a\) - see Figure 6. Inside an incompressible fluid, pressure drops with height according to the Pascal equation (6), so that just below the surface, \(\mathcal{P} \approx \mathcal{P}_{0}-\rho g h\), where \(\mathcal{P}_{0}\) is the background (e.g., atmospheric) pressure. This means that at \(a<<h\) the pressure variation along the concave surface (called the meniscus) of the liquid is negligible, so that according to the Young-Poisson equation (13), the sum \(\left(1 / R_{1}+1 / R_{2}\right)\) has to be virtually constant along the surface. Due to the axial symmetry of the problem, this means that the surface has to be a part of a sphere. From the contact angle definition, the radius \(R\) of the sphere is equal to \(a / \cos \theta_{\mathrm{c}}-\) see Figure 6. Plugging this relation into Eq. (3) with \(\mathcal{P}_{1}-\mathcal{P}_{2}=\rho g h\), we get the following result for \(h\) : \[\rho g h=\frac{2 \gamma \cos \theta_{\mathrm{c}}}{a} .\] In hindsight, this result might be obtained more directly - by requiring the total weight \(\rho g V=\) \(\rho g\left(\pi a^{2} h\right)\) of the lifted liquid’s column to be equal to the vertical component \(F \cos \theta_{\mathrm{c}}\) of the full surface tension force \(F=p p\), acting on the perimeter \(p=2 \pi a\) of the meniscus. Using the definition (11) of the capillary length \(a_{\mathrm{c}}\), Eq. (16a) may be represented as the so-called Jurin rule: \[h=\frac{a_{\mathrm{c}}^{2}}{a} \cos \theta_{\mathrm{c}} \leq \frac{a_{\mathrm{c}}^{2}}{a}\] according to our initial assumption \(h>>a\), Eq. (16) is only valid for narrow tubes, with radius \(a<<a_{\mathrm{c}}\).

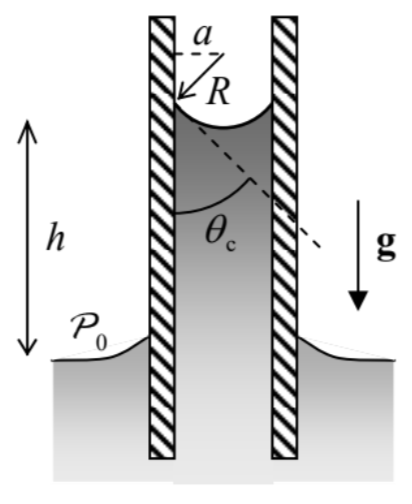Figure 8.6. Liquid’s rise in a vertical capillary tube.

This capillary rise is the basic mechanism of lifting water with nutrients from roots to the branches and leaves of plants, so that the tallest tree heights correspond to the Jurin rule (16), with \(\cos \theta_{c}\) \(\approx 1\), and the pore radius \(a\) limited from below by a few microns, because of the viscosity effects restricting the fluid discharge - see Sec. 5 below.

---

\({ }^{8}\) Indeed, if the \(\gamma\) of the interface of certain two fluids is negative, it self-reconfigures to decrease \(U_{\mathrm{i}}\), i.e. increase \(\left|U_{\mathrm{i}}\right|\), by increasing the interface area, i.e. fragments the system into a macroscopically-uniform solution.

\({ }^{9}\) This equality follows from the general relation (7.30), with the stress tensor elements expressed by Eq. (2), but in this simple case of the net stress force \(d \mathbf{F}=\left(\mathcal{P}_{1}-\mathcal{P}_{2}\right) d \mathbf{A}\) parallel to the interface element vector \(d \mathbf{A}\), it may be even more simply obtained just from the definition of work: \(\delta \mathscr{W}=d \mathbf{F} \cdot \delta \mathbf{r}\) at the virtual displacement \(\delta \mathbf{r}=\mathbf{n} \delta r\).

\({ }^{10}\) This general formula may be verified by elementary means for a sphere of radius \(r\) (for which \(R_{1}=R_{2}=r\) and \(d A=r^{2} d \Omega\), so that \(\delta(d A) / d A=\delta\left(r^{2}\right) / r^{2}=2 \delta r / r\) ), and for a round cylindrical interface of radius \(R\) (for which \(R_{1}=r\), \(R_{2}=\infty\), and \(d A=r d \varphi d z\), so that \(\left.\delta(d A) / d A=\delta r / r\right)\). For more on curvature, see, for example, M. do Camo, Differential Geometry of Curves and Surfaces, \(2^{\text {nd }}\) ed., Dover, \(2016 .\)

\({ }^{11}\) This result (not to be confused with Eq. (15), called Young’s equation) was derived in 1806 by Pierre-Simon Laplace (of the Laplace operator/equation fame) on the basis of the first analysis of the surface tension effects by Thomas Young (yes, the same Young who performed the famous two-slit experiment with light!) a year earlier.