8.1: Function of Endpoint Position

We’ll now think of varying the action in a slightly different way. (Note: We’re using Landau's notation.) Previously, we considered the integral of the Lagrangian over all possible different paths from the initial place and time \(\begin{equation}
q^{(1)}, t_{1}
\end{equation}\) to the final place and time \(\begin{equation}
q^{(2)}, t_{2}
\end{equation}\)

and found the path of minimum action. Now, though, we’ll start with that path, the actual physical path, and investigate the corresponding action as a function of the final endpoint variables, given a fixed beginning place and time.

Taking one degree of freedom (the generalization is straightforward), for a small path variation the incremental change in action

\begin{equation}
\delta S=\left[\frac{\partial L}{\partial \dot{q}} \delta q\right]_{t_{1}}^{t_{2}}+\int_{t_{1}}^{t_{2}}\left(\frac{\partial L}{\partial q}-\frac{d}{d t} \frac{\partial L}{\partial \dot{q}}\right) \delta q d t
\end{equation}

(Recall that first term comes from the calculus of variations when we allow the end point to vary -- it’s exactly the same point we previously discussed in the brachistochrone problem of fastest time for a given horizontal distance, allowing the vertical position of the endpoint to be a free parameter.)

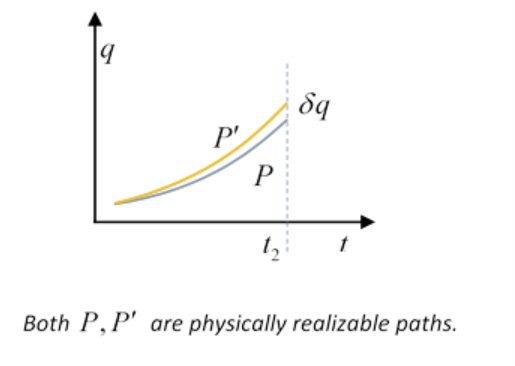
With the incremental variation, we’ve gone from the physical path P (followed by the system in configuration space from \(\begin{equation}
q^{(1)}, t_{1} \text { to } \left.q^{(2)}, t_{2}\right)
\end{equation}\) to a second path \(\begin{equation}
P^{\prime}
\end{equation}\) beginning at the same place and time, and ending at the same time \(\begin{equation}
t_{2}
\end{equation}\) as P, but at a slightly different place \(\begin{equation}
q^{(2)}+\delta q\left(t_{2}\right)
\end{equation}\).

Both paths \(\begin{equation}
P, P^{\prime}
\end{equation}\) are fully determined by their initial and final positions and times, so \(\begin{equation}
P, P^{\prime}
\end{equation}\) must correspond to slightly different initial velocities. The important point is that since both paths describe the natural dynamical development of the system from the initial conditions, the system obeys the equations of motion at all times along both paths, and therefore the integral term in the above equation is identically zero.

Writing \(\begin{equation}
\delta q\left(t_{2}\right)=\delta q, p^{(2)}=p
\end{equation}\) the action, regarded as a function of the final position variable, with the final time fixed at \(\begin{equation}
t_{2}
\end{equation}\), has the differential

\begin{equation}
\delta S\left(q^{(2)}, t_{2}\right)=\left[\frac{\partial L}{\partial \dot{q}} \delta q\right]_{t_{1}}^{t_{2}}=p^{(2)} \delta q^{(2)}=p \delta q
\end{equation}

For the multidimensional case, the incremental change in the action on varying the final position variable is given by (dropping the superscript)

\begin{equation}
\partial S / \partial q_{i}=p_{i}
\end{equation}