18.2: Damped Driven Oscillator

The linear damped driven oscillator:

\begin{equation}
\ddot{x}+2 \lambda \dot{x}+\omega_{0}^{2} x=(f / m) e^{i \Omega t}
\end{equation}

(Following Landau’s notation here—note it means the actual frictional drag force is \(2 \lambda m \dot{x}\))

Looking near resonance for steady state solutions at the driving frequency, with amplitude \(b\), phase lag \(\delta\), that is,

\(x(t)=b e^{i(\Omega t+\delta)}\), we find

\begin{equation}
b e^{i \delta}\left(-\Omega^{2}+2 i \lambda \Omega+\omega_{0}^{2}\right)=(f / m)
\end{equation}

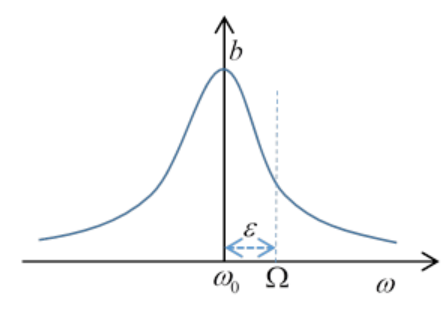
For a near-resonant driving frequency \(\Omega=\omega_{0}+\varepsilon\), and assuming the damping to be sufficiently small that we can drop the \(\varepsilon \lambda\) term along with \(\varepsilon^{2}\), the leading order terms give

\begin{equation}
b e^{i \delta}=-f / 2 m(\varepsilon-i \lambda) \omega_{0}
\end{equation}

so the response, the dependence of amplitude of oscillation on frequency, is to this accuracy

\begin{equation}
b=\frac{f}{2 m \omega_{0} \sqrt{\left(\Omega-\omega_{0}\right)^{2}+\lambda^{2}}}=\frac{f}{2 m \omega_{0} \sqrt{\varepsilon^{2}+\lambda^{2}}}
\end{equation}

(We might also note that the resonant frequency is itself lowered by the damping, but this is another second-order effect we ignore here.)

The rate of absorption of energy equals the frictional loss. The friction force \(2 \lambda m \dot{x}\) on the mass moving at \(\dot{x}\) is doing work at a rate:

\begin{equation}
2 \lambda m \dot{\dot{x}}^{2}=\lambda m b^{2} \Omega^{2}
\end{equation}

The half width of the resonance curve as a function of driving frequency \(\Omega\) is given by the damping. The total area under the curve is independent of damping.

For future use, we’ll write the above equation for the amplitude as

\(b^{2}\left(\varepsilon^{2}+\lambda^{2}\right)=\frac{f^{2}}{4 m^{2} \omega_{0}^{2}}\)